原文:https://blog.csdn.net/jasonzzj/article/details/52017438
本文只讨论Logistic回归的交叉熵,对Softmax回归的交叉熵类似。
交叉熵的公式

以及J(θ)对J(θ)对参数θ的偏导数(用于诸如梯度下降法等优化算法的参数更新),如下:

交叉熵损失函数

假设函数(hypothesis function)定义为:

因为Logistic回归问题就是0/1的二分类问题,可以有
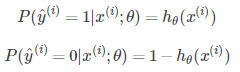
现在,我们不考虑“熵”的概念,根据下面的说明,从简单直观角度理解,就可以得到我们想要的损失函数:我们将概率取对数,其单调性不变,有:

那么对于第i组样本,假设函数表征正确的组合对数概率为:
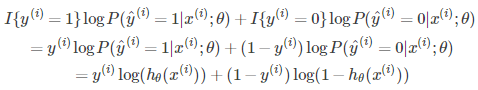
其中,I{y(i)=1}和I{y(i)=0}为示性函数(indicative function),简单理解为{ }内条件成立时取1,否则取0。
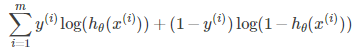
由以上表征正确的概率含义可知,我们希望其值越大,模型对数据的表达能力越好。而我们在参数更新或衡量模型优劣时是需要一个能充分反映模型表现误差的损失函数(Loss function)或者代价函数(Cost function)的,而且我们希望损失函数越小越好。由这两个矛盾,那么我们不妨领代价函数为上述组合对数概率的相反数: 
交叉熵损失函数的求导
这步需要用到一些简单的对数运算公式,这里先以编号形式给出,下面推导过程中使用特意说明时都会在该步骤下脚标标出相应的公式编号,以保证推导的连贯性。
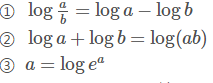
在这里涉及的求导均为矩阵、向量的导数(矩阵微商)。交叉熵损失函数为:
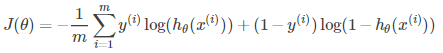
其中,

由此,得到 :

这次再计算J(θ)对第j个参数分量θj求偏导:

这就是交叉熵对参数的导数:
