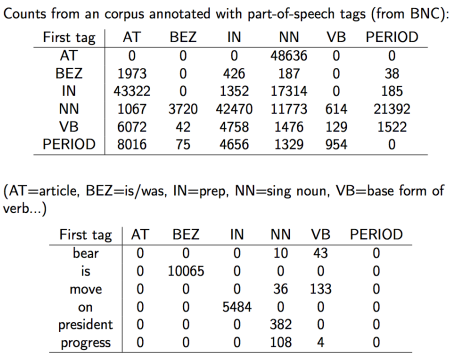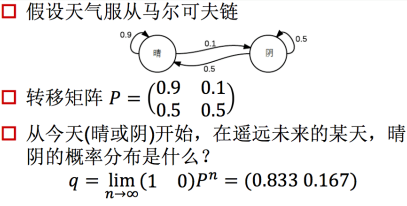
在初始状态确定的情况下,(1 0)状态下,马尔科夫链的结果最终会趋于稳态分布。
即最终结果会得到一个固定的稳态分布。



没有办法给出完整的判断,这个时候就需要多一条马尔科夫链。
先设置一个牛市和熊市的马尔科夫链,然后牛市对应涨跌,熊市也对应涨跌。从而得到一个双层结构的马尔科夫链。
能观测到的最外侧的涨跌(显性的状态集合),而牛市和熊市没办法直接观测得到为隐式。
通过能观测的显性求解出整个双层马尔科夫链集合,这就是隐马尔科夫链。

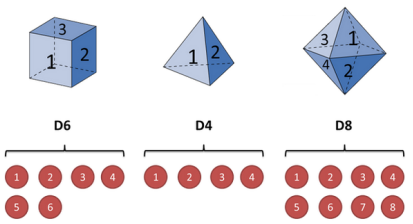
由于每次掷骰子的时候只能得到黑盒输出的数字(可见状态链:1,6,8,5,4),
并不能直接知道是哪一种骰子得到的,只能推测出(隐形状态链:D4,D6,D8,D6,D4)。(根据上述可见状态连的结果来对应推测出隐形状态链)
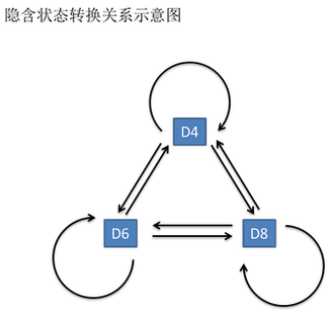
在这里假设三种骰子出现的概率都是三分之一,因此上图中每条线上,他们之间的转换概率都是三分之一。
每一种骰子都能产生出一种,因此在上述隐式马尔科夫链外面加上一层显式的喷射(投射)的可见状态并对应相应的概率值。
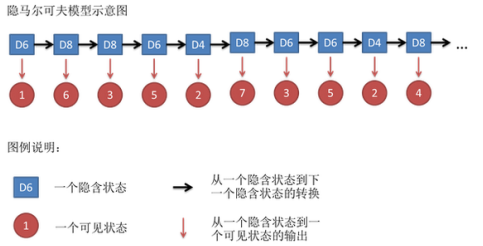
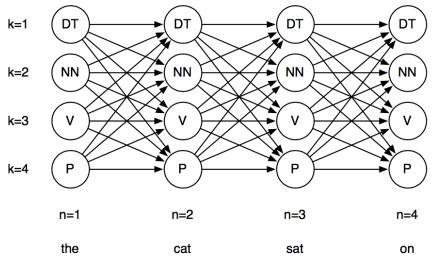
展开的隐式马尔科夫链,横向是时间表示每个节点就是每一次选的骰子并掷出一定的数值。
此图类似于展开的RNN中有一个记录状态,每个状态能射出不同的数值。

三种问题中,观测结果是一定会已知能观测出来的。

问题1:Evaluation:O表示可以直观看到的观测序列;模型为λ=(A状态转移矩阵,B观测的概率分布,π初始概率分布)。然后计算出在模型确定情况下观测值出现的概率。
问题2:Recognition:已知观测序列和模型,如何选择一个相关的状态序列(就是隐层的马尔科夫链)Q来最好地描述观测值的产生。
例如,HMM在语音识别问题中,同一句话有不同的语音,通过不同的语音想要识别出背后真正传达的含义。
问题3:Training:已知观测值,如何通过调整模型的参数(模型未知)找到最好的A,B,π使得该模型对应的观测序列值最大化。
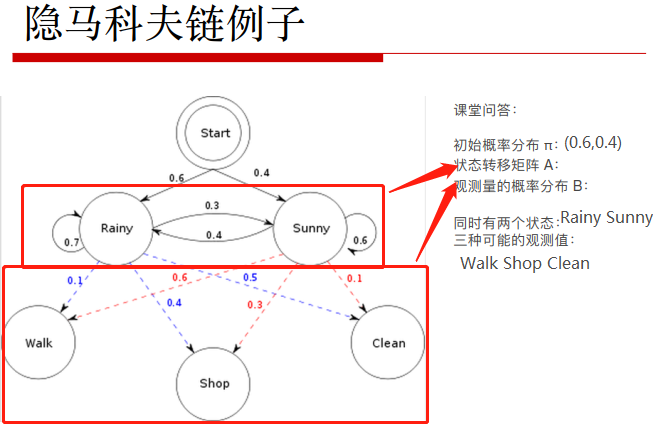


三种观测值和两种天气状态的组合情况:2^3=6种,分别进行计算。例如:
P(R,R,R,W,S,C) = P(1R) P(W|1R) P(2R) P(S|2R) P(3R) P(C|3R) = 0.6*0.1*0.7*0.4*0.1*0.5
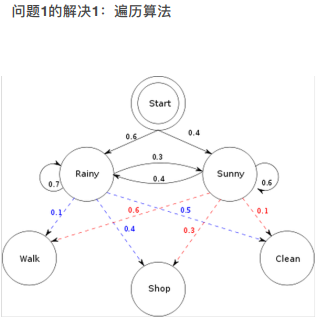
将所有可能的路径,全部算出来相应的概率值。

先预设Q的值,然后猜测对于一个样本序列Q而言,此概率P(O|Q,λ)的大小:将所有时间节点都连乘起来。b表示q状态喷射出来的观测值相应概率。

P(O,Q|λ)表示模型已知情况下,O,Q显示观测值和隐式值同时出现的概率。
可以将所有隐Q加起来
P(Q|λ)表示出此天气的权重
虽然思路简单,但时间复杂度较高,计算量很大。
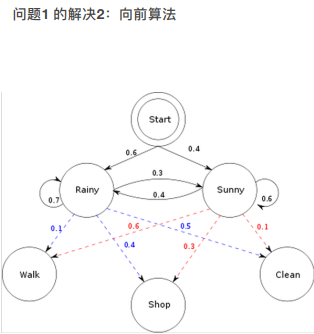
t =1,w
P(W,R) = P(1R)*P(W|R) = 0.6*0.1 = 0.06
P(W,S) = P(1S)*P(W|1S) = 0.4*0.6 = 0.24
t =2, S
P(1W,2S,2R) = [P(1W,1R)*P(2R|1R)+P(1W,1S)*P(2R|1R)]*P(2S|2R) =
以此类推,之后的情况按照时间累计,需要考虑之前的情况。
好处在于:时间复杂度相比遍历算法降低了。时间复杂度随着时间的变长会越来越低,因为是基于之前算好的进行计算的。
遍历算法(图论的形式)不仅有横向的(每天不同的状态值)还有纵向的(每天不同状态下不同的观测值)。时间复杂度是指数形式。

观测到时间t的时候的可能观测值,以及t时刻预测状态值为Sj的概率。利用前向变量作为中介值写出两条公式。
bjot+1为喷发值,πi为本身的初始概率。
在t+1时刻喷发值j的概率bjot+1,计算出递推结果αj(t+1)
最后把所有可能性都加起来。
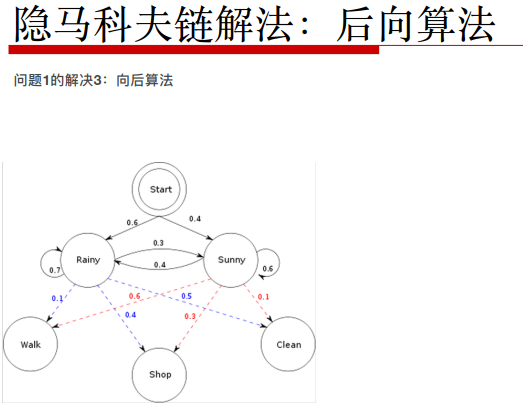
从最后一个状态慢慢往前推导。后向变量β
初始化init:β3(R)=1或者β3(S)=1然后进行递推。(A状态转移,B模型喷射值,π初始值)
已知最后一个观测值为O3=C,由于后向观测值为一个确定的数值,所以初始值不像前向计算时初始化为一定的概率了,这里直接初始化为1。
β2(R) =状态转移α(R-R) bR(O3=C) β3(R) + a(R-S) bS(O3=C) β3(S) = 0.7*0.5*1+0.3*0.1*1
以此类推,利用递推公式,求出所有的β1(R),β1(S),β1(R)
P(W,S,C) = πR bR(O1=W)β1(R) + πS bS(O1=W) β1(S)

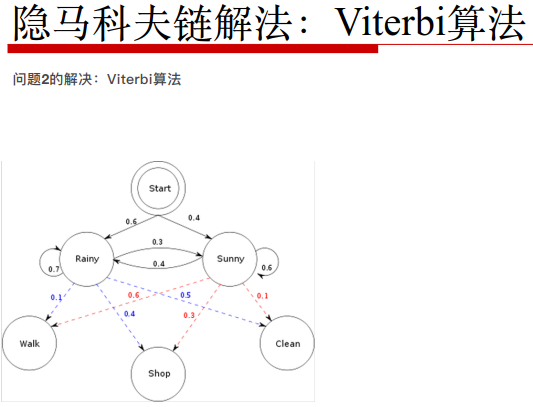
类似图论。已知最后的结果是W,S,C,利用暴力搜索的模式遍历所有的中介点。探求以什么中介点组合能使得最后结果的概率P(W,S,C)最高。
init:δ1(R) = πR * bR(O1=W) =0.06
δ1(S) = πS * bS(O1=W) =0.06
路径:状态存储量 φ1(R) = 0 φ1(S) = 0
δ2(R) = max[δ1(R) * a(R-R) * bR(O2=S)] = 得到此最大值的是rainny还是sunny,记录到φ当中。
δ2(S) = max[δ1(R) * a(R-R) * bR(O2=S)] =

viterbi算法相当于动态规划算法。本质就是利用空间换取时间。用更多的存储量将中间点都存储下来,并且算下一层的时候直接通过中间点往后进行计算。
viterbi每次都是依照前一次的进行计算,并将前一次中能够使得这一次达到最好值的中介点记录下来。
好处:1)不必再做烦琐的遍历了,每次都把最好的结果保存下来。
2)可以防止进入贪心算法的误区:因为贪心算法每次都拿最好的,这样容易拿到的是局部最优。而动态规划算法一直关注的是全局最优。
viterbi变量δj(t)中j为让δj(t)能取到最大概率的状态
递推公式induction中δj(t+1)是由δj(t)aij最大的值乘上当前状态的喷射值概率bjOt+1
回溯过程backtracking:由于我们的目标并不是求出最大值,而是求出取得最大值的路径,即天气的最优排列表。
当仅仅知道观测值,别的什么都不知道的时候来推导模型的解法如下:
解决此方法得到的只能是局部最优解,找不到全局的。因为在只有观测值的情况下,对模型参数的任何猜测都有一个先天的限制(自定义的一个初始化范围内)。
两种解决方法:1)gradient techniques梯度下降
2)Baum-Welch reestimation(EM)最难的方法



最终会稳定到HMM的一个最优值:maximum likelihood estimate of HMM
得到的是局部最优点,很复杂。

利用viterbi算法自己写出词性标注Tag:将一句话中的所有单词标注出它的词性。
本例采用英语(因为可以直接利用空格进行分词,用中文还需要利用jieba分词在词与词之间加上空格)
标注词性之后可以用于NLP后续的名词提取。
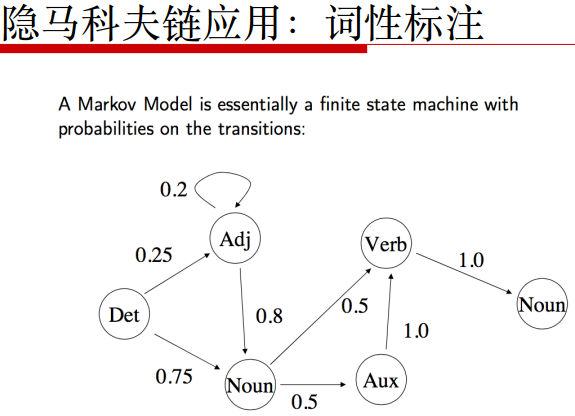
根据词性写出一种句子。
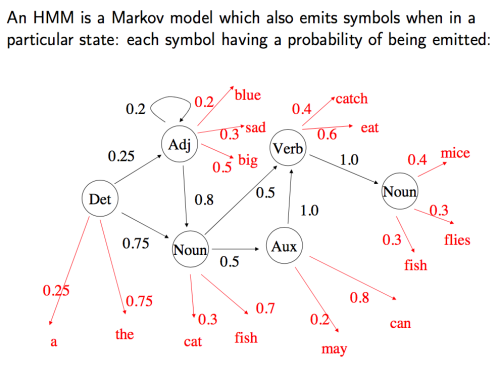
每种词性能喷射出具体的单词。然后通过观测值和这个HMM模型推测出内层的具体链条构造。
此时做的是毫无意识的推测,这是上面描述的最难的问题三,此法非常低效且复杂度高。
利用语料库corpus总结标好句子与词性之间的关系,利用总结学习好的句子模型再对新的句子进行标注。这就将上述的问题三降维到了问题二。
然后计算出所有概率得到完整的HMM模型λ=(π,A,B),然后将新句子放入此模型中进行标注。

在单词确定(句子给定的条件下),出现某一标注的概率P(t1...tN|w1...wN)利用贝叶斯方程来求解。
链式法则chain rule

词性标注转换分布P(t1...tN)
单词喷射分布

求出A和B的分布。AT为A的起始值
如果有tag和相应的sentences就是问题1