递归
在讲解关于递归的主要内容前,先让我们看一个gif动图。

这个动图呢很像我们平时生活中的开多个门的场景。门要开就需要关,我们开了多扇门就相应的意味着我们要关掉多少们,而且最先开的门往往最后关,最后开的门往往最先开,回想一下是不是这样子的。
以上就是递归在我们平时生活中的一个案例,接下来就是一个编程中的案例。
对于求5!,我们呢,经常用的一种方法是这样子的:
def factorial(num): # 求阶乘函数
resolution = 1
for i in range(1,num):
resolution *= num
return resolution
另一种使用递归的方式如下:
def factorial(num): # 求阶乘函数
if num == 1:
return 1
else:
return num * factorial(n - 1)
有没有觉得使用递归的方式比上面那种方法的代码更整洁、更漂亮。
回归到主题——递归,我们可以发现代码中有两句起关键性作用的代码:num == 1 和 else ,在递归中,前者属于基线条件,也就是打破递归循环的条件,具体为什么,待会儿看一段代码;后者属于递归条件,也就是函数调用函数自身。
def count_down(i):
print(i)
count_down(i - 1)
我们仔细观看这段代码,它具有了递归条件,但是不具备基线条件,当我们运行时,就会发现它会一直运行下去,成了一个无限循环,这个就是上面说的为什么要具有基线条件的原因。
接下来,我们就会谈到一个跟递归相关的数据结构:栈——调用栈。
说到栈呢,平时生活中的一个常见的例子就是我们堆放桌子上的数,当我们一本一本把书堆起来后,我们再拿书时,往往最上面的一本书是我们最后放上去的,而我们最下面一本书却是我们最先放上去的。这个就是栈的特点之一:先进后出(也叫后进先出)。
调用栈,顾名思义,就是计算机每执行一个代码中的函数就会将其先压栈,再出栈,也就是,把函数放进去,等到该函数执行完了,再把它拿出去。
接下来请看一段代码:
def sum_num(num):
if num == 1:
return 1
else:
return num + sum_num(num - 1)
if __name__ == '__main__':
print(sum_num(5))
上面的代码就是一个求0—5的整数的和,是一个使用递归的典型例子。
通过对代码的解读,我们可以得到如下的结果:
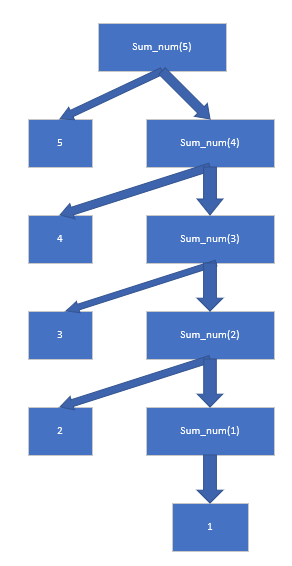
请读者自己对着代码的每一步执行思考一下,是不是这样子的。
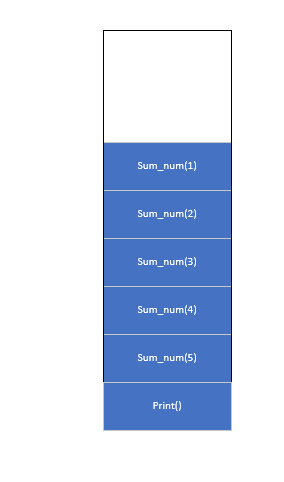
接下来,就是压栈的过程,如图:
然后就是一个出栈的过程,如图:
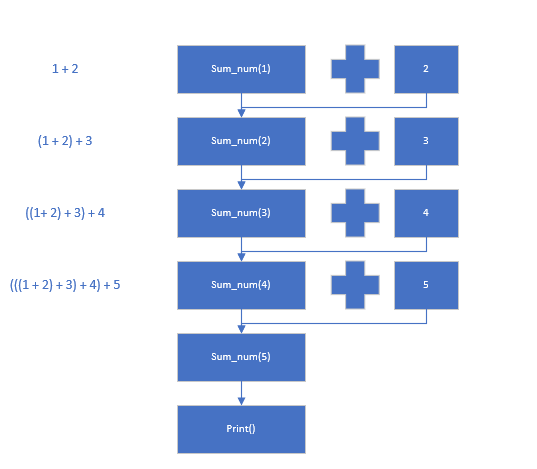
其运行的过程呢,就是通过每一步函数的执行,函数调用自身,进行函数的入栈,在达到递归的基线条件时,便进行出栈,按照先进后出的原则。
可能读了以上还不太明白,这里再出一个使用的递归的编程题,读者可以自行尝试一下,答案就在下方。
题目:编写一个递归函数来计算列表包含的元素数。
答案:
def count(list):
if list == []:
return 0
else:
return 1 + count(list[1:])
怎么样,有没有点感觉了。
最后,小编写作不易,麻烦读者点赞关注一下,您的赞将会是小编更新的最大动力,谢谢。