归并排序

1.思想

　　将初始序列划分成长度为1的子序列，再将子序列两两地按大小重新合并成有序序列，不断地像这样合并下去，直到最后得到初始长度的有序序列

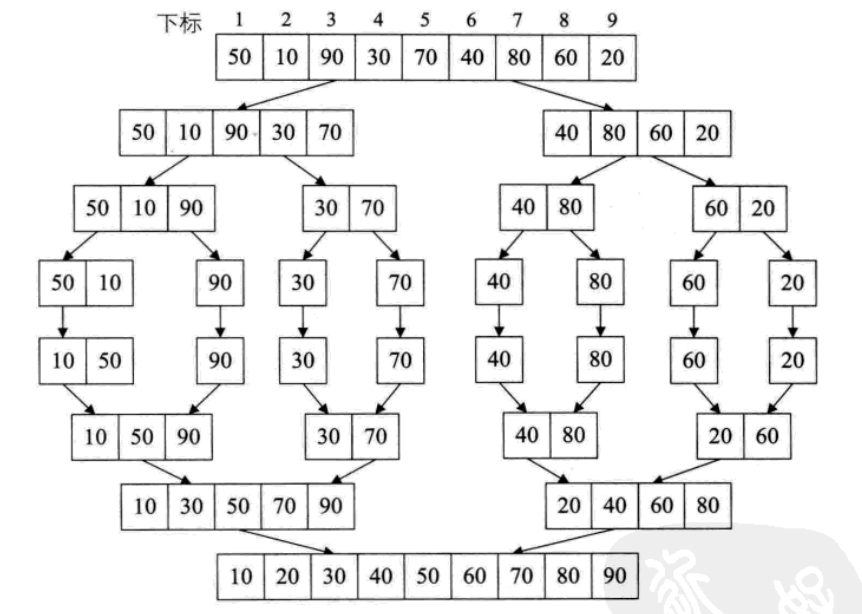
2.代码实现

合并有序序列的函数：

/*序列nums分别在区间[left,mid]和[mid+1,right]是有序的，将这两个区间有序地合并起来*/
void mergeTwoSortedArray(vector<int>& nums, int left, int mid, int right, vector<int>& temp)
{
    int i = left, j = mid + 1;
    int k = 0;
    while (i <= mid && j <= right)
        temp[k++] = (nums[i] <= nums[j]) ? nums[i++] : nums[j++];
    while (i <= mid)
        temp[k++] = nums[i++];
    while (j <= right)
        temp[k++] = nums[j++];
    for (i = 0; i < k; ++i)
        nums[left + i] = temp[i];
}

2.1递归版：

void sortMerge(vector<int>& nums, int left, int right, vector<int>& temp)
{
    if (left < right)
    {
        int mid = left + (right - left) / 2;
        sortMerge(nums, left, mid, temp);
        sortMerge(nums, mid + 1, right, temp);
        mergeTwoSortedArray(nums, left, mid, right, temp);
    }
}

void sortMerge(vector<int>& nums)
{
    vector<int> temp(nums.size());
    sortMerge(nums, 0, nums.size() - 1, temp);
}

2.2非递归版（迭代版）：

转载自：https://blog.csdn.net/jacketinsysu/article/details/52472364

其实归并排序就是从最短子序列开始，两两按大小重组，不断重复

步长step：子序列长度

初始序列：8 7 6 5 4 3 2 1

第一遍，步长为1，将相邻的子序列有序合并（注意加粗黑体）：
8 7 6 5 4 3 2 1 
7 8 5 6 4 3 2 1 
7 8 5 6 3 4 2 1 
7 8 5 6 3 4 1 2

第二遍，步长为2，将相邻的子序列有序合并（注意加粗黑体）：
5 6 7 8 3 4 1 2
5 6 7 8 1 2 3 4

第三遍，步长为4，将相邻的子序列有序合并（注意加粗黑体）：
1 2 3 4 5 6 7 8

void sortMerge_nonrecursive(vector<int>& nums)
{
    int n = nums.size();
    vector<int> temp(n);
    for (int step = 1; step < n; step *= 2)
    {
        for (int i = 0; i < n; i += 2 * step)
            /*一定要使用min()函数的原因：防止越界*/
            mergeTwoSortedArray(nums, i, min(i + step - 1, n - 1), min(i + 2 * step - 1, n - 1), temp);
    }
}

时间复杂度

　　每一轮合并子序列操作的平均时间复杂度为O(n)（图中的一行），又由完全二叉树深度可知（共几轮），所以总的平均时间复杂度为O(nlogn)（最好情况和最坏情况都是）

空间复杂度

　　用到了大小为n的辅助数组，递归版还用到了深度为logn的栈空间，所以O(n)

稳定性

　　这种分成子序列再合并排序的过程可以保证相同元素排序前后的相对顺序不变，所以是稳定的