(LCA)问题(倍增法)
前言
其实本身并没有写这篇博客的打算,主要原因是看了很多的博客,然后感觉写那篇博客的大佬写的实在是太好了,自愧不如。
但,问题在于,我虽然已经完全理解了(LCA)倍增的真谛,但是在代码实现方面我还是没有能够达到自己写的地步。
所以,个人感觉还是有必要写一篇博客的。
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
(LCA)前置
链式前向星
对于几乎所有的图论题目而言,存图几乎是必备的一项操作,而链式前向星则是存图的一种方式,由于其优秀的时空复杂度,使得链式前向星成为了对于图论题目最常用的一种存图方式。
在使用链式前向星的前提之下,我们通常使用(DFS),(BFS)来进行图的遍历。
因此,我们同样可以借助(DFS)来理解链式前向星。
(DFS)算法的实现过程可以这样理解:
1.以当前点作为起点,在所有与该起点连接的边中随便找一条,然后跳到这条边的终点上。
2.再将当前跳到的点当作起点,重复1。
3.若跳到某一点后,没有以这个点为起点的边了,就原路返回到之前的起点上,找一条与这条不同的边,再跳到它的终点上。
显然,(DFS)标记的是着一条边所指向的终点,以及一个点的出度。
好巧不巧,
链式前向星的结构中真他更好包括了这亮点,链式前向星的结构定义如下:
struct node{
int to;
int next;
}edge[maxn];
链式前向星是以边为单位进行储存。其中,成员to表示这条边的终点,而next就比较重要了,表示本条边的起点相同的前一条边,在edge数组中的下标,如果这条边的起点是第一次出现的,则置为0。也就是说,链式前向星的next属性,像链表一样,将途中起点相同的边连在了一起。就像下面这个图。
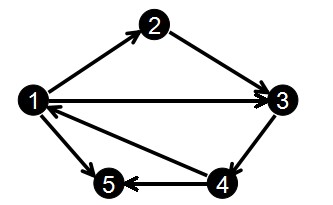
那么我们就可以得到一个edge数组。
当我们想要得到一条边的终点时,就调用edge[i].to,当我们想要知道这个起点连接的其他边时,就可以调用edge[i].next。那么现在的问题就是如何快速地求得next的属性。
解决方法:
再定义一个数组head,head[i]表示最近一次输入的以i为起点的边在edge数组中的下标。
我们来看代码:
#include<iostream>
using namespace std;
const int maxn=1000;
struct node
{
int to;
int next;
}edge[maxn];
int head[maxn];
int cnt=1;
void add(int from,int t)
{
edge[cnt].to=t;
edge[cnt].next=head[from];
head[from]=cnt++;
}
bool s[maxn];
void dfs(int x)
{
s[x]=true;
printf("%d ",x);
for(int i=head[x];i!=0;i=edge[i].next)
{
if(!s[edge[i].to])
dfs(edge[i].to);
}
}
int main()
{
int u,v,w;
int n;
cin>>n;
while(n--)
{
cin>>u>>v;
add(u,v);
}
dfs(1);
return 0;
}
(ST)算法
(ST)算法在更多的情况下其实应该应用与(RMQ)问题(区间最值问题)之中。
但是(LCA)倍增算法同样需要用到与(ST)算法相似甚至几乎相同的代码思路和代码构造,所以可以前置学习一下。
在(RMQ)问题中,(ST)算法就是倍增的产物。
给定一个长度为(N)的数列(A)。
(ST)算法能够在(O(nlogn))的时间复杂度下预处理,之后以(O(1))的时间复杂度在线回答数列(A)中下标在(l~r)之间的最大值是多少。
设(F[i,j])表示数列(A)中下标在子区间([i,i+2^j-1])里的数的最大值,也就是从(i)开始的(2^j)个数的最大值。
递推边界是(F[i,0]=A[i])
有公式:
// 区间最值
void ST_prework() { // st算法预处理
for(int i = 1 ;i<=n ; i++ ) {
f[i][0] = a[i] ; // 处理边界 [i,i] 的最大值就是 a[i]
}
int t = log(n)/log(2) + 1 ; // 这里是枚举右端点
for(int j =1 ; j<t ; j++){
for(int i = 1 ;i<=n-(1<<j)+1 ;i++) {
f[i][j] = min(f[i][j-1] ,f[i+(1<<(j-1))][j-1]) ;
}
}
}
当询问任意区间([l,r])的最值时,我们先计算一个(k)使(k)满足(2^k<r-l+1leq2^{k+1}),也就是使2的(k)次幂小于区间长度的前提下的最大的(k).
那么,从(l)开始的(2^k)个数和以(r)结尾的(2^k)个数这两段一定覆盖了整个区间([l,r])的最大值。
这两段的最大值分别是(F[i,k])和(F[r-2^k+1,k]),二者中较大的那个就是整个区间的最大值。
int ST_query(int l ,int r){ // 查询 区间 [l,r] 之间的最值
int k = log(r-l+1)/log(2);
return max(f[l][k],f[r-(1<<k)+1][k]) ;
}
(LCA)本体
两个关键理论
相信大家都做过这样一道题,大概意思表达的是任何一个正整数都可以表示成两个不同的2的次幂的加和。
如果(c)是(a)和(b)的(LCA),那么(c)的所有祖先同样是(a)和(b)的公共祖先,但不是最近的。
(LCA)中的(ST)(预处理)
在(ST)算法中,
我们维护了一个数组(dp[i][j]),表示的是以下标(i)为起点的长度为(2^j)的序列的信息。
然后用动态规划的思想求出了整个数组。
而通过倍增求(LCA)要跳2的幂次方层。
这就与(dp)数组的(j)下标的定义不谋而合。
所以我们定义倍增法中的(dp[i][j])为:结点(i)的向上(2^j)层的祖先。
//fa表示每个点的父节点
int fa[100],DP[100][20];
void init()
{
//n为结点数,先初始化DP数组
for(int i=1;i<=n;i++)
dp[i][0]=fa[i];
//动态规划求出整个DP数组
for(int j=1;(1<<j)<=n;j++)
for(int i=1;i<=n;i++)
DP[i][j]=DP[DP[i][j-1]][j-1];
}
上述代码完成了整个函数的预处理部分,下面则是查询函数。
查询函数
这个函数的参数就是要查询的两个结点(a)和(b)。
在函数中我们应指定(a)是深度较大的那一个((b)也可以),这样方便操作。
然后让(b)不断向上回溯,知道跟(a)处于同一深度。
然后让(a)和(b)同时向上回溯,直到二者相遇。
这个过程不难理解:
对于第一次回溯,我们要做的是尽可能大得跳,以便于使两个点到达相同的深度。
因为我们已经知道了两个点的深度差。
而对于第二次回溯,我们就是随便乱跳,如果大了,就一个一个得往回跳,知道找到(LCA)。
//查询函数
int LCA(int a,int b)
{
//确保a的深度大于b,便于后面操作。
if(dep[a]<dep[b])
swap(a,b);
//让a不断往上跳,直到与b处于同一深度
//若不能确保a的深度大于b,则在这一步中就无法确定往上跳的是a还是b
for(int i=19;i>=0;i--)
{
//往上跳就是深度减少的过程
if(dep[a]-(1<<i)>=dep[b])
a=dp[a][i];
}
//若二者处于同一深度后,正好相遇,则这个点就是LCA
if(a==b)
return a;
//a和b同时往上跳,从大到小遍历步长,遇到合适的就跳上去,不合适就减少步长
for(int i=19;i>=0;i--)
{
//若二者没相遇则跳上去
if(dp[a][i]!=dp[b][i])
{
a=dp[a][i];
b=dp[b][i];
}
}
//最后a和b跳到了LCA的下一层,LCA就是a和b的父节点
return dp[a][0];
}
以上就是倍增的主要思路。
(LCA)代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
struct zzz {
int t, nex;
}e[500010 << 1]; int head[500010], tot;
void add(int x, int y) {
e[++tot].t = y;
e[tot].nex = head[x];
head[x] = tot;
}
int depth[500001], fa[500001][22], lg[500001];
void dfs(int now, int fath) {
fa[now][0] = fath; depth[now] = depth[fath] + 1;
for(int i = 1; i <= lg[depth[now]]; ++i)
fa[now][i] = fa[fa[now][i-1]][i-1];
for(int i = head[now]; i; i = e[i].nex)
if(e[i].t != fath) dfs(e[i].t, now);
}
int LCA(int x, int y) {
if(depth[x] < depth[y]) swap(x, y);
while(depth[x] > depth[y])
x = fa[x][lg[depth[x]-depth[y]] - 1];
if(x == y) return x;
for(int k = lg[depth[x]] - 1; k >= 0; --k)
if(fa[x][k] != fa[y][k])
x = fa[x][k], y = fa[y][k];
return fa[x][0];
}
int main() {
int n, m, s; scanf("%d%d%d", &n, &m, &s);
for(int i = 1; i <= n-1; ++i) {
int x, y; scanf("%d%d", &x, &y);
add(x, y); add(y, x);
}
for(int i = 1; i <= n; ++i)
lg[i] = lg[i-1] + (1 << lg[i-1] == i);
dfs(s, 0);
for(int i = 1; i <= m; ++i) {
int x, y; scanf("%d%d",&x, &y);
printf("%d
", LCA(x, y));
}
return 0;
}