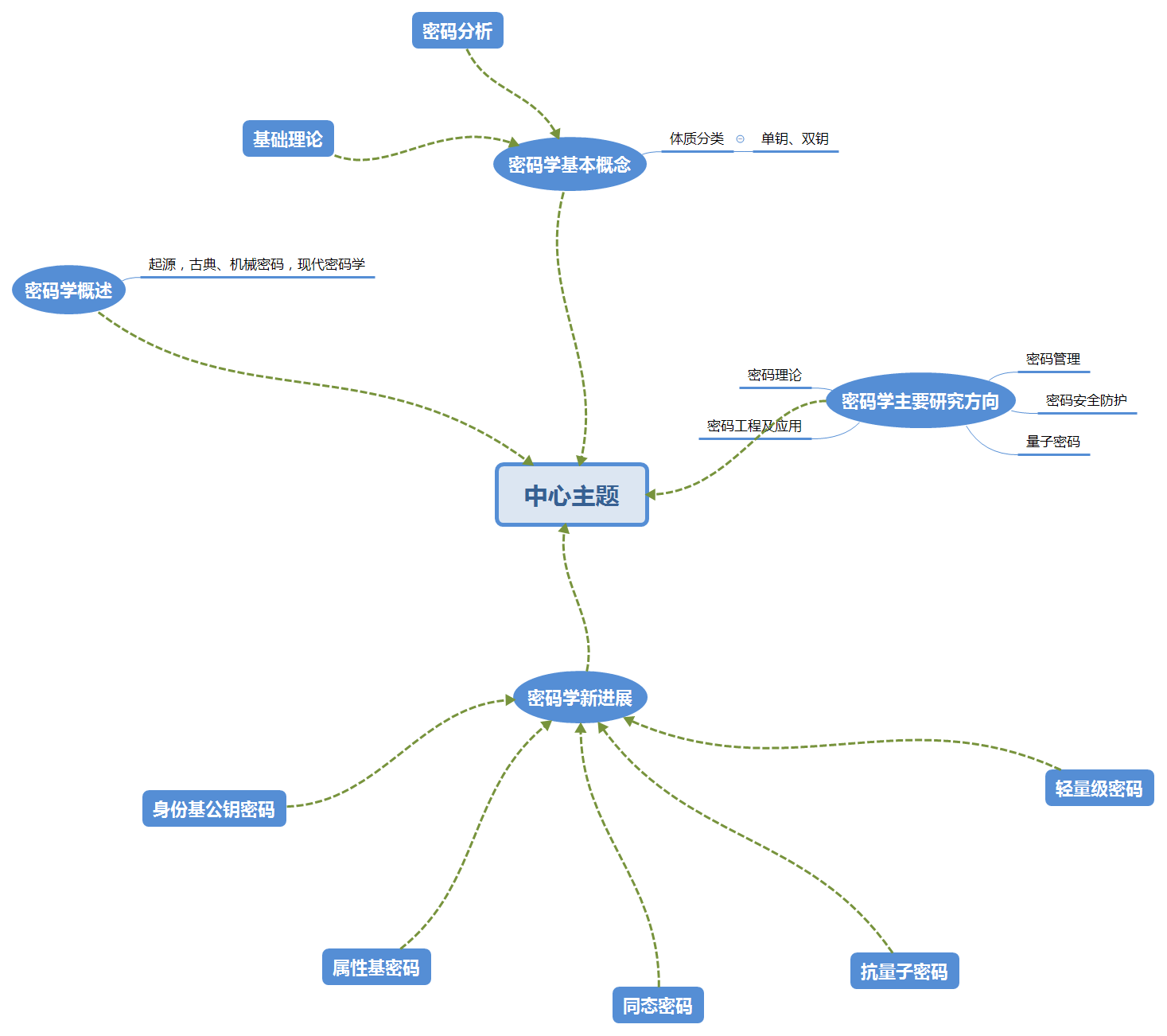
(一)内容概述
2.1 密码学概述
2.1.1 密码的起源。古代岩画、古文字、隐写术等都属于密码的起源。
2.1.2 古典密码。古典密码主要应用了代换、置换的思路,前者引申出凯撒密码、维吉尼亚密码、普莱费尔密码,后者引申出栅格置换、矩形置换。注意:弗纳姆密码是一次一密密码,明文和密钥作异或运算得到密文。
2.1.3 机械密码。
1,ENIGMA密码机:利用精妙的机械结构生成密文、明文。
2,其他机械密码机。
2.1.4 现代密码学。
现代密码学鼻祖:Claude Shannon。
1,保密通信系统的数学模型。
2,信息隐藏:也称为信息隐匿或信息隐形,秘密信息被嵌入表面上看起来无害的宿主信息中,攻击者无法直观地判断它所监视的信息中是否含有秘密信息。
信息加密:利用单钥或双钥算法把明文变换成密文并通过公开信道送到接受者手里。
3,密码系统与通信系统:通信系统是对抗系统中存在的干扰,实现有效、可靠的信息传输。密码系统本质上也是一种信息传输系统,是普通通信系统的对偶系统。
4,Shannon信息论。
组合概念:由简单易于实现的密码系统进行组合,构造较复杂的、密钥量较大的密码系统。Shannon曾给出两种组合方式,即加权和法和乘积法。
扩散概念:将每一位明文和密钥尽可能迅速地散布到较多位密文数字中去,以便隐蔽明文的统计特性。
混淆概念:使明文和密文、密钥和密文之间的统计相关性极小化,使统计分析更为困难。
2.1.5 密码学面临的挑战。
1,云计算/存储对密码学的新挑战。
2,大数据对密码学的新挑战。
3,物联网对密码学的新挑战。
4,新型计算机对密码学的新挑战。
5,区块链技术对密码学的新挑战。
2.2 密码学基本概念。
保密学分为密码编码学和密码分析学。加密和解密算法的操作通常都是在一组密钥的控制下进行的,分别称为加密密钥和解密密钥。加密密钥和解密密钥相同(或本质上相同),称为单钥或对称密码体质。加密密钥和解密密钥不同,称为非对称密码体质或双钥。
2.2.1 密码体质分类。
两大类:单钥密码体质和双钥密码体质。
单钥:Alice、Bob通信,双方必须采用相同的密钥进行加密解密。必须将密钥安全的送达通信双方。
双钥:pk:公钥,公开的;sk:私钥,秘密的。Alice向Bob传送加密信息时,Alice用Bob的公钥加密,Bob只能用自己的私钥解密。
2.2.2 密码分析。
1,密码攻击类型:
a,唯密文破译:仅仅对密文进行分析。
b,已知明文破译:除了截获密文外,还有明文、密文对。
c,选择明文破译:分析者可以选定任何明文密文对进行分析,以确定未知的密钥;
d,选择密文攻击:分析者可以利用解密机,按他所选的密文解密出相应的明文。
2,技术方法:
1,穷举攻击法。完全试凑法。
2,数学攻击法。
3,物理攻击法。
2.2.3 密码学理论基础。
1,整数分解。2,模运算。3,有限域。4,欧几里得算法。5,中国剩余定理。6,椭圆曲线。
2.2.4 国内外密码算法概览。
1,序列密码。密钥流和明文进行异或运算,即输出密文流,解密过程同理。
2,分组密码。分组密码是基于单密钥的对称密码体质,常见的有代替—置换网络。
3,公钥密码。
a,RSA公钥密码算法:基于 大整数分解难题。
b,Rabin公钥密码算法:RAS衍生公钥密码算法。
c,ElGamal公钥密码算法。
d,椭圆曲线公钥密码算法。