SIFT算法：KeyPoint找寻、定位与优化

SIFT算法：DoG尺度空间生产 

SIFT算法：KeyPoint找寻、定位与优化

SIFT算法：确定特征点方向 

SIFT算法：特征描述子

---

目录：

1、找寻

2、定位

3、优化

---

1 KeyPoint找寻

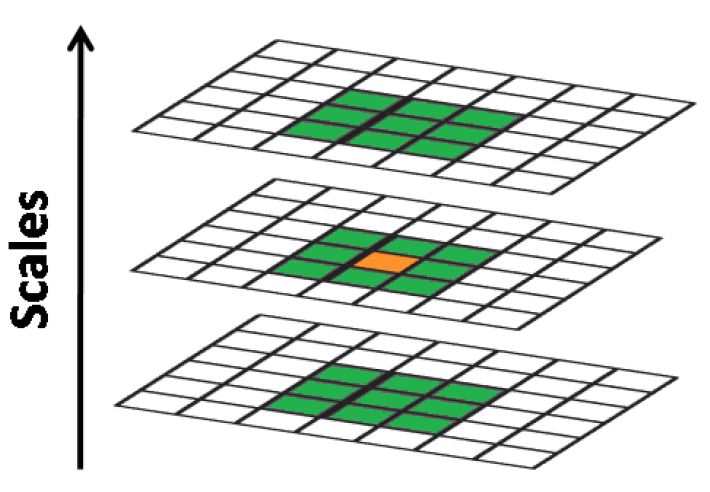
　　极值的检测是在DoG空间进行的，检测是以前点为中心，3pixel*3pixel*3pixel的立方体为邻域，判断当前点是否为局部最大或最小。如下图所示，橘黄色为当前检测点，绿色点为其邻域。因为要比较当前点的上下层图像，所以极值检测从DoG每层的第2幅图像开始，终止于每层的倒数第2幅图像（第1幅没有下层，最后1幅没有上层，无法比较）。

2 KeyPoint定位

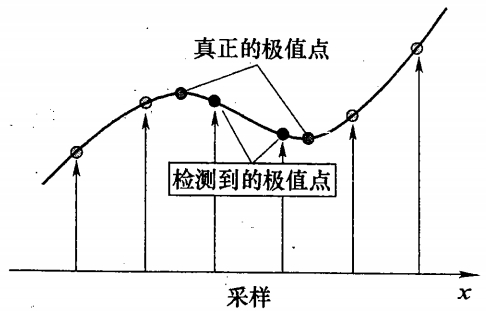
　　以上极值点的搜索时在离散空间中进行的，检测到的极值点并不是真正意义上的极值点。如下图所示，连续空间中极值与离散空间的区别。通常通过插值的方式，利用离散的值来插值，求取接近真正的极值的点。

对于一维函数，利用泰勒级数，将其展开为二次函数：

f(x) ≈ f(0) + f^'(0)x + f^''(0)x²

对于二维函数，泰勒展开为：

矩阵表示为：

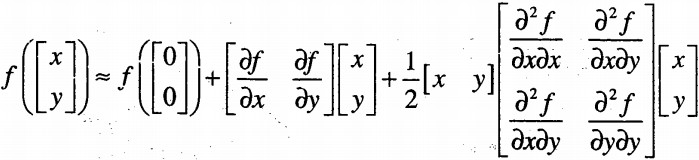
矢量表示为：

当矢量为n维时，有：

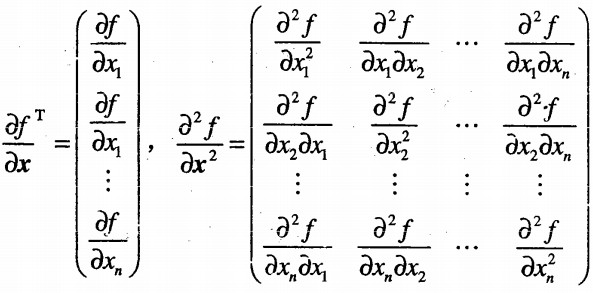
求取f(x)的极值，只需求取∂f/∂x = 0。对于极值，x,y,σ三个变量，即为三维空间。利用三维子像元插值，设其函数为D(x, y, σ)，令x = (x, y, σ)^T，那么在第一节中找到的极值点进行泰勒展开为（式-1）如下：

其中D为极值点的值，∂D^T/∂x为在极值点各自变量的倒数，∂²D/∂x²为其在展开点相应的矩阵。对上式求导，另∂D(x)/∂x = 0，结果如下式，对应的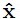（为了表示方便，ˆx代替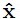）向量即为真正极值点偏离插值点的量。求解得（式-2）如下：

最终极值点的位置即为插值点x+ˆx，且多次迭代可以提高精度（一般为5次迭代）。

问题 1：

　　《图像局部不变性特征与描述》中提到，对于偏移量ˆx任何方向上偏移大于0.5的特征点，要删除该点。

　　对于Lowe的原文为：If the offset ˆx is larger than 0.5 in any dimension, then it means that the extremum lies closer to a different sample point. In this case, the sample point is changed and the interpolation performed instead about that point.

　　本人英语水平有限，个人认为原作者并未说要删除此类点，只是说这个点偏移了，所以需要插值来进行替换。且在OpenCV sift的源码中，并未删除上述类型的点，在vlfeat的开源代码中，也未删除上述点。

3 KeyPoint优化

　　对KeyPoint定位后，要剔除一些不好的KeyPoint，那什么是不好的KeyPoint的呢？

1. DoG响应较低的点，即极值较小的点。
2. 响应较强的点也不是稳定的特征点。DoG对图像中的边缘有较强的响应值，所以落在图像边缘的点也不是稳定的特征点。一方面图像边缘上的点是很难定位的，具有定位的歧义性；另一方面这样的点很容易受到噪声的干扰变得不稳定。

　　对于第一种，只需计算矫正后的点的响应值D(ˆx)，响应值小于一定阈值，即认为该点效应较小，将其剔除。将（式-2）带入（式-1），求解得：

在Lowe文章中，将|D(ˆx)|<0.03（图像灰度归一化为[0,1]）的特征点剔除。

　　对于第二种，利用Hessian矩阵来剔除。一个平坦的DoG响应峰值在横跨边缘的地方有较大的主曲率，而在垂直边缘的地方有较小的主曲率。主曲率可以通过2×2的Hessian矩阵H求出：

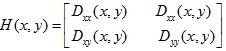
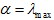　　D值可以通过求临近点差分得到。H的特征值与D的主曲率成正比，具体可参见Harris角点检测算法。为了避免求具体的值，我们可以通过H将特征值的比例表示出来。令为最大特征值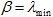，为最小特征值，那么：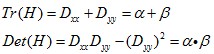

 

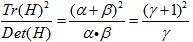
　　Tr(H)表示矩阵H的迹，Det(H)表示H的行列式。令表示最大特征值与最小特征值的比值，则有：

　　

　　上式与两个特征值的比例有关。随着主曲率比值的增加，也会增加。我们只需要去掉比率大于一定值的特征点。Lowe论文中去掉r=10的点。

---

参考资料：

1. David G. Lowe Distinctive Image Features from Scale-Invariant Keypoints 
2. 王永明 王贵锦 《图像局部不变性特征与描述》