目录:
1、数学定义
2、过程描述
3、算法简介
4、总结
1、数学定义
局部搜索是解决最优化问题的一种启发式算法。对于某些计算起来非常复杂的最优化问题,比如各种NP完全问题,要找到最优解需要的时间随问题规模呈指数增长,因此诞生了各种启发式算法来退而求其次寻找次优解,是一种近似算法(Approximate algorithms),以时间换精度的思想。局部搜索就是其中的一种方法。
对于组合问题,给出如下定义:

其中,S为搜索空间(解空间),其中的每一元素都是问题一个可能解。解决组合问题,即是找到一个s* ∈ S,使得目标函数f值最小。s*称为全局最优解。
对于邻域动作定义如下:
![]()
邻域动作是一个函数,通过这个函数,对当前解s,产生其相应的邻居解集合。例如:对于一个bool型问题,其当前解为:s = 1001,当将邻域动作定义为翻转其中一个bit时,得到的邻居解的集合N(s)={0001,1101,1011,1000},其中N(s) ∈ S。同理,当将邻域动作定义为互换相邻bit时,得到的邻居解的集合N(s)={0101,1001,1010}.
2、过程描述
局部搜索算法从一个初始解开始,通过邻域动作,产生其邻居解,判断邻居解的质量,根据某种策略,来选择邻居解,重复上述过程,至到达终止条件。不同局部搜索算法的区别就在于:邻域动作的定义和选择邻居解的策略,也是决定算法好坏的关键(集中性和发散性,Intensification and Diversification)。
3、算法简介
对于优化问题相关算法有如下分类:
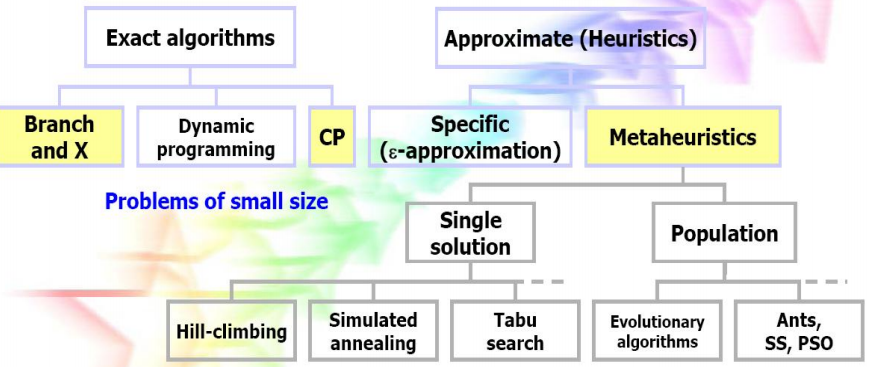
下文分别简单介绍几个局部搜索相关算法,也是基于个体的启发式算法(Single solution)。
3.1 爬山法(Hill-climbing)
爬山法与Iterative Improvement的思想是一样的,区别在于前者寻找最大值,后者寻找最小值。一种完全的贪心的思想,有更好的,则选择更好的,没有更好的,则终止。

流程如上图所示,判断当前解s的邻居解质量,若其中有比当前解更好的解,则s = Improve(N(S)),令当前解等于邻居解中质量最好的解,重复上述过程,直至邻居解中没有更好的解为止。
缺点:很容易陷入局部极值,最终解的好坏与初始解的选择有很大关系。
3.2 模拟退火(Simulated annealing)
为了防止陷入局部最优,模拟退火算法以一定概率接受比当前解差的解,接受差解的概率随着迭代次数的增加而下降,或者说是随着温度T的下降而下降。先看流程图,如下:

该算法从一个初始解开始,这个初始解可以是随机选择的,也可以是启发式方式得到的,并初始化一个温度。在每次迭代过程中,从当前解的邻居解中随机的选择一个解,若随机选择的一个邻居解比当前解的质量好,则替换当前解,若质量比当前解差,则以一定的概率接受这个差解,来替换当前解。最后更新温度T,进行下一次迭代。
- 接受差解的概率是一个关于 T 和 (f(s') - f(s)) 的函数。函数形式为:p(T,s',s) = exp(- ( f(s') - f(s) ) / T)
- 温度T随着搜索的过程而减小,由上述表达式可知,随着T减小(对于最小值问题,解的质量最好,f(x)的值越小),接受差解的概率越小,因此模拟退火算法将慢慢收敛于一个 simple iterative improvement algorithm。
- 该算法由两个阶段:random walk and iterative improvement,这两者体现了启发式算法核心思想:Diversification and Intensification,前者提供了一个广阔的搜索空间,后者使其收敛于最小值(或者局部最小值)。
3.3 禁忌搜索(Tabu/Taboo Search, TS)
禁忌搜索,顾名思义,禁止某些选项。TS算法通过引入一个灵活的存储结构和相应的禁忌准则来避免暂时的迂回搜索。
举个简单的例子:一日三餐,为了寻找最好的搭配。
- 当10月1日(初始日)中午随机选了几样东西作为食物,早上:面包,中午:米饭,晚上:面条;
- 当10月2日(第二次迭代),在众多相近的选择中(邻居解集合),我选择效果最好的,早上:面包,中午:面条,晚上:面条,
- 2日整体效果比1日好,那么其变化为:中午由 米饭->面条, “中午:米饭”这个属性被我记住了(禁忌表),在接下来几天(禁忌长度)中,对于邻居解中任何有“中午:米饭”的解,我将不会考虑,除非该解比历史最好的效果都好(解禁条件)。
通过上例,引出一下几个概念:
禁忌表(tabu list):记录被禁止的属性,其值为禁忌长度(tabu tenure),该长度范围内,该属性被禁止。
解禁条件(aspiration condition):当含有禁忌属性的解,效果好于历史最好解时,我们选择这个被禁忌的解,其他情况,被禁忌的解不予考虑。

对于禁忌算法,每次一迭代都要更新禁忌表,禁忌表的维护决定了算法的快慢,对于禁忌长度,可以是恒定的长度,也可以是动态的长度。具体的细节,可以参见博文的图染色问题。
3.4 Explorative Local Search methods
注:此节中,伪代码中提到的 LocalSearch(s) 为简单的局部搜索,上面三种算法的任意一种。c
3.4.1 迭代局部搜索(Iterated Local Search, ILS)
在局部搜索得到的局部最优解上,加入了扰动,再重新进行局部搜索。其思想是:物以类聚,好的解之间会有一些共性,所以在局部最优解上做扰动,比随机的选择一个初始解在进行局部搜索,效果更好。
过程描述如下:

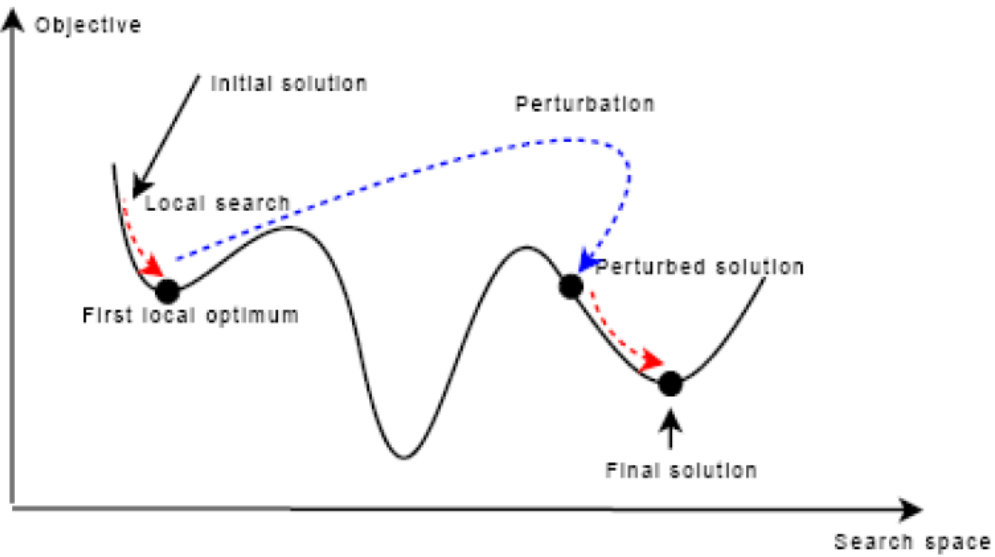
其伪代码如下:

对与其中的接受准则:这里采用了模拟退火中的概率函数:
![]()
3.4.2 变邻域搜索(Variable Neighborhood Search, VNS)
- 变邻域搜索算法的主要思想是:采用多个不同的邻域进行系统搜索。首先采用最小的邻域搜索,当无法改进解时,则切换到稍大一点的邻域。如果能继续改进解,则退回到最小的邻域,否则继续切换到更大的邻域。
- 变邻域搜索的特点是利用不同的动作构成的邻域结构进行交替搜索,在集中性和疏散性之间达到很好的平衡。
- 其思想可以概括为“变则通”。
过程描述如下:

每变换一次邻域,相对于切换了搜索的地形(landscape)。效果如下:
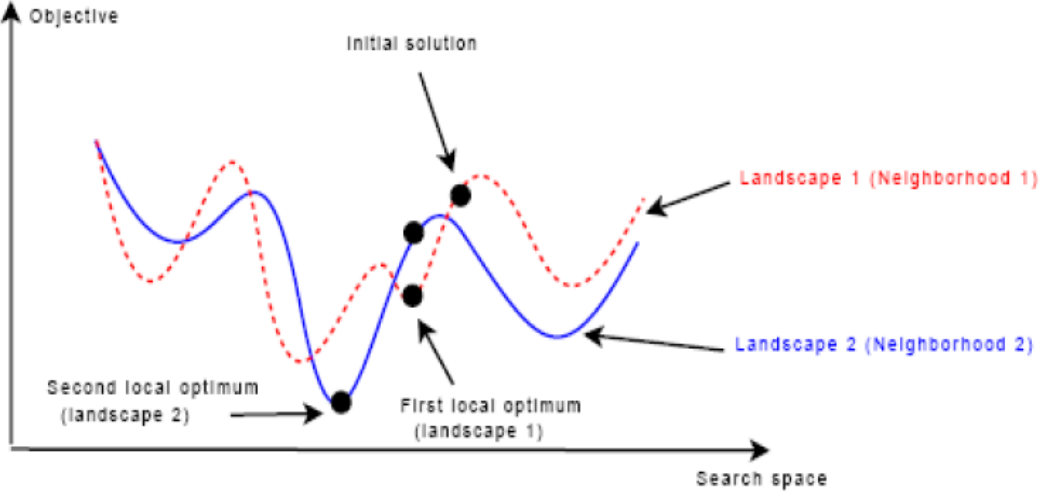
伪代码如下图:

4、总结
启发式算法蕴含着许多人生哲学,它虽不是数学方法,其思想更类似于人类解决问题的思想和一些人生中总结的道理,值得好好体会。最后用网上一段描述局部搜索的例子来作为总结:
为了找出地球上最高的山,一群有志气的兔子们开始想办法。
- 兔子朝着比现在高的地方跳去。他们找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是Iterative Improvement,它不能保证局部最优值就是全局最优值。
- 兔子喝醉了。他随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,他渐渐清醒了并朝最高方向跳去。这就是模拟退火。
- 兔子们知道一个兔的力量是渺小的。他们互相转告着,哪里的山已经找过,并且找过的每一座山他们都留下一只兔子做记号。他们制定了下一步去哪里寻找的策略。这就是禁忌搜索。
- 兔子们吃了失忆药片,并被发射到太空,然后随机落到了地球上的某些地方。他们不知道自己的使命是什么。但是,如果你过几年就杀死一部分海拔低的兔子,多产的兔子们自己就会找到珠穆朗玛峰。这就是遗传算法。
参考资料:
- Metaheuristicsin Combinatorial Optimization: Overview and Conceptual Comparison
- 华中科技大学吕志鹏老师:启发式优化课件