6-1 Topological Sort (25 分)
编写程序以在有向图中找到拓扑顺序。
功能格式:
bool TopSort( LGraph Graph, Vertex TopOrder[] );
其中LGraph定义如下:
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV;
PtrToAdjVNode Next;
};
typedef struct Vnode{
PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv;
int Ne;
AdjList G;
};
typedef PtrToGNode LGraph;
拓扑顺序应该被存储在TopOrder[]其中,TopOrder[i]是i将得到的序列中的第一个顶点。如果图中有一个循环,则拓扑排序不能成功 - 在这种情况下TopSort必须返回false; 否则返回true。
请注意,拓扑顺序可能不是唯一的,但是判断的输入保证了结果的唯一性。
法官示例程序:
#include <stdio.h>
#include <stdlib.h>
typedef enum {false, true} bool;
#define MaxVertexNum 10 /* maximum number of vertices */
typedef int Vertex; /* vertices are numbered from 0 to MaxVertexNum-1 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV;
PtrToAdjVNode Next;
};
typedef struct Vnode{
PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv;
int Ne;
AdjList G;
};
typedef PtrToGNode LGraph;
LGraph ReadG(); /* details omitted */
bool TopSort( LGraph Graph, Vertex TopOrder[] );
int main()
{
int i;
Vertex TopOrder[MaxVertexNum];
LGraph G = ReadG();
if ( TopSort(G, TopOrder)==true )
for ( i=0; i<G->Nv; i++ )
printf("%d ", TopOrder[i]);
else
printf("ERROR");
printf("
");
return 0;
}
/* Your function will be put here */
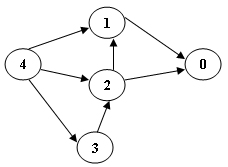
样本输入1(对于图中所示的图表):
5 7 1 0 4 3 2 1 2 0 3 2 4 1 4 2
样本输出1:
4 3 2 1 0
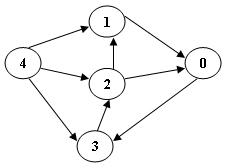
样本输入2(对于图中所示的图表):
5 8 0 3 1 0 4 3 2 1 2 0 3 2 4 1 4 2
样本输出2:
ERROR
bool TopSort( LGraph Graph, Vertex TopOrder[] )
{
int Indegree[Graph->Nv];//建立入度表
int Queue[Graph->Nv];//建立队列存储入队为0的节点
int pre=0, tail=0;//队首和队尾
PtrToAdjVNode p;
for(int i=0; i<Graph->Nv; i++)
Indegree[i] = 0;//初始化入度表为0
for(int i=0; i<Graph->Nv; i++){//构造入度表
for(p=Graph->G[i].FirstEdge; p!=NULL; p=p->Next)
Indegree[p->AdjV]++;
}
for(int i=0; i<Graph->Nv; i++){//将入度为0的节点入队
if(!Indegree[i])
Queue[tail++] = i;
}
int num = 0;//记录入队的数目
while(pre < tail){
int pos = Queue[pre];
TopOrder[num++] = Queue[pre++];
for(p=Graph->G[pos].FirstEdge; p!=NULL; p=p->Next){
int index = p->AdjV;
--Indegree[index];//将出队的节点,即删除的节点的邻接节点入队减1
if(!Indegree[index])//若更新入度后入度为0则入队
Queue[tail++] = index;
}
}
if(num == Graph->Nv)
return true;
else
return false;
}