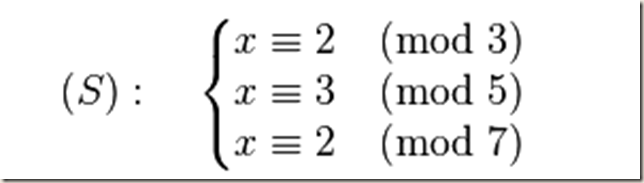韩信点兵（中国剩余定理）

中国剩余定理是数论中的一个关于一元线性同余方程组的定理，说明了一元线性同余方程组有解的准则以及求解方法。又称为孙子定理，“韩信点兵”“求一术”“鬼谷算”“隔墙算”“剪管术”“秦王暗点兵”“物不知数”等名称。

例如：物不知数原文：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

宋朝数学家秦九韶对“物不知数”问题作出了完整系统的解答。还被别人编成了《孙子歌决》：

三人同行七十希，五树梅花廿一支，七子团圆正半月，除百零五使得知

这个歌诀给出了模数为3,、5、7时候的同余方程的秦九韶解法。意思是：将除以3的余数乘以七十，将除以5的余数乘以21，将除以7的余数乘以15，全部加起来后除以105，得到的余数就是答案。比如说“物不知数”中的例子，使用以上的方法计算就得到：

70*2+21*3+15*2 = 233 = 2*105+23

答案就是23.

形式描述：用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：

有解的判定条件，并用构造法给出了在有解情况下解的具体形式。

中国剩余定理说明：假设整数m₁、m₂、m₃…m_n 两两互质，则对任意的整数：a1、a2、… 、an，方程组S有解，并且通解可用如下方式构造得到：

例子：

使用中国剩余定理求解上面的“物不知数”便可以理解《孙子歌诀》中的含义。这里的线性同余方程组是：

程序实现：

package crt;


public class Crt {
    static int [] m = {3,5,7}; //模数，条件互质
    static int [] a = {2,3,2};   //余数
    static int [] Mi = {1,1,1};   // 
    static int M = 1;
    static int firstNum = 0;
    static int x = 0;
    static int [] t = new int [3];
     public static  void GetTvalue(){
        
        for(int i=0;i < t.length;i++)
        {
            int temp = 0;
            while((Mi[i]*temp - 1)%m[i] != 0)
            {
                temp++;
            }
            t[i] = temp;
            
        }
        
    }
    public static void main(String[] args) {
        
        
        
        for(int i = 0;i < m.length;i++)
        {    
            M = M*m[i];
        }
        for(int j =0;j < Mi.length;j++)
        {
            Mi[j] = M/m[j];
        }
        
        GetTvalue();
        
        for(int k = 0;k < 3 ;k++)
        {
            x = x + a[k]*t[k]*Mi[k];
        }
        
        
        firstNum = x%M;
        for(int k = 0;k<t.length;k++)
        {
            System.out.println(t[k]);
        }
        System.out.println(x);
        
        System.out.println(firstNum);
    }
        
}