TSP,即旅行商问题,又称TSP问题(Traveling Salesman Problem),是数学领域中著名问题之一。假设有一个旅行商人要拜访N个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP问题是一个NPC问题。TSP的历史很久,最早的描述是1759年欧拉研究的骑士周游问题,即对于国际象棋棋盘中的64个方格,走访64个方格一次且仅一次,并且最终返回到起始点。
假设现在有四个城市:A,B,C,D,E,他们之间的代价如下图所示,可以存成二维表的形式

同样的问题,在车间计划调度领域还有另一个相似的问题:车间生产A,B,C,D,E五中产品,不同产线之间切换需要准备时间用于更换模具,切换物料,由于自动化水平比较高,制造时间比较稳定,不同产品切换时间不一样,如果必须把所有的产品都生产完成,那么该如何选择生产顺序,使所有的切换的时间最小或者总的完工时间最小?计划调度领域这个问题有个专业名称:Sequence-dependent setup times problem,TSP中的距离矩阵等同于JSP中的准备时间矩阵。
假设制造工时都是2小时,产品切换准备时间矩阵如上图,相同产品不需要准备时间:
生产A切换B需要2小时,A切换C需要10小时,A切换D需要8小时,A切换E需要3小时,……,
生产B切换A需要1小时,B切换C需要2小时,B切换D需要5小时,B切换E需要7小时,……,
……
早期的研究者使用精确算法求解该问题,常用的方法包括:分枝定界法、线性规划法、动态规划法等。
但是,随着问题规模的增大,精确算法将变得无能为力,因此,在后来的研究中,国内外学者重点使用近似算法或启发式算法,
主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等,

具体这些算法不一一介绍,本文将本文重点讲解易普优APS如果进行建模求解;
第一步:工艺路线建模
建模比较简单,制造BOM设置1道工序,制造时间为2小时。

第二步:产品切换时间矩阵
TSP问题中的城市距离矩阵,在APS系统中可以转换为产品切换矩阵,具体设置如下图所示。
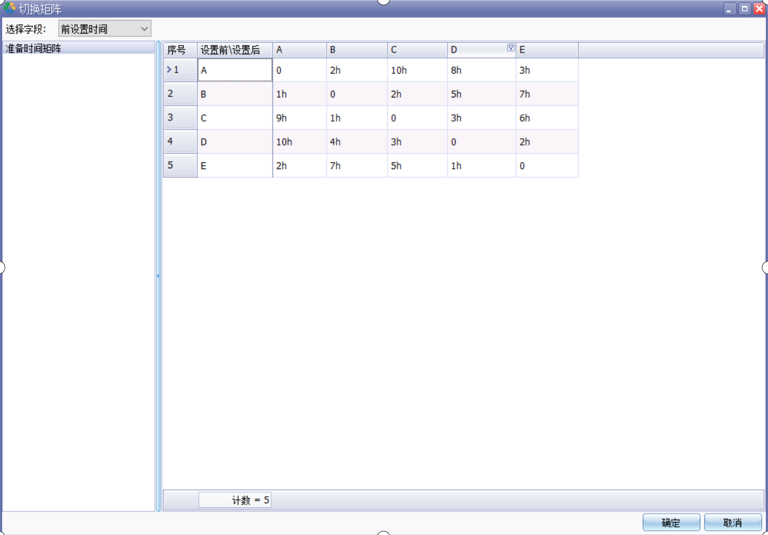
在APS系统中产品切换矩阵以关系数据表示,上图5x5矩阵在系统中保存为25行数据,行数据如下图所示。

第三步:设置生产订单
APS系统中将去每一个城市作为一项工作任务或者一个工单,5个城市则需要在系统中导入5个工单。

第四步:组合优化算法,结果甘特图直观展示
易普优APS最优化算法库支持多种优化求解算法,包括遗传算法、模拟退火法、蚁群算法、禁忌搜索,贪心算法等,可以快速求解TSP问题,如下是文章TSP问题的最优解
A-->E-->D-->C-->B--A,其中准备时间为9小时,制造时间为10小时,完工最小时间为19小时;下一篇文章将通过APS系统演示求解基于坐标位置的TSP问题。

其他APS高级计划排程系统相关扩展阅读:
3、 APS演绎饭局模型(通俗的告诉您为什么ERP计划与APS计划的区别)
4、烽火集团PCBA企业应用易普优APS实现智能计划排产案例
7、易普优高级计划排程Light版助力中小企业实现精益化计划
9、易普优APS混合遗传算法求解FJSP柔性车间调度最优化问题