数据结构优化建图
有的时候我们需要将编号在 ([L, R]) 中的每一个点都向编号在 ([L', R']) 中的每一个点连边。这时暴力连边会使复杂度达到 (O(n^2m)) 的级别,因此我们需要对区间分块统一处理。
我们需要建立一棵入树和一棵出树。入树中的节点表示某些边可以连到区间中的任意点;出树的节点表示区间中的所有点都能向外连某些边。
首先我们对这些块与块之间进行处理:
-
入树的所有父亲向儿子连0边(能到达([1, 10]),必然能到达 ([1, 5]) 和 ([6, 10]));
-
出树的所有儿子向父亲连0边(能从 ([1, 5]) 中的某些点出发,必然能从 ([1, 10]) 的某些点出发);
-
入树的所有点向出树的对应点连0边(能到达([1, 10])的所有点,必然能从([1, 10])中的某些点出发)。
(简而言之,入树是一棵外向树,出树是一棵内向树,树树连边)
然后当我们连边 ([l, r] -> [l', r'])的时候,我们把出树中的 ([l, r]) 分成若干段,连向一个中转节点 (p_i),然后将 (p_i) 连向入树中的 ([l',r']) 所含的若干段。
最后把整体当作一个图来处理即可。能保证最终的所有叶子节点的信息正确。(所有操作从入点开始做)
因为入树都向出树对应节点连无关紧要的边,使得出树的信息最终会被入树信息更新,但是不保证入树信息被出树信息更新。因此我们只需从入树开始,就能保证最终两棵树信息一致。
例题:CF786B Legacy
题意:支持一对多连边,求单源最短路。
模板题。直接找到入树中的 (s) 节点开始跑最短路即可。最终入树中的叶子节点和出树中的叶子节点的信息都是正确的。
例题:P3588 [POI2015]PUS
题意:已知一个序列的部分数,以及知道某些区间中的某些数的最小值比剩下的所有数都大。要求判无解或构造序列。
差分约束+线段树优化建边。
一些降低编程复杂度的小技巧:
-
可以把建入树和建出树分开来写,记录一下一棵树的节点数 (tot), 然后连树间的边就直接((cur - tot) ~ ~ ->~ ~ cur) 就好。
-
建树的时候可以直接记录一下每个位置对应的叶子节点编号,方便单点查询。
void build_i(int L, int R, int &cur) {
cur = ++ttot;
if (L == R) return i_p[L] = cur, h[cur] = a[L], isg[cur] = a[L] > 0, void();
int mid = (L + R) >> 1;
build_i(L, mid, ls[cur]), build_i(mid + 1, R, rs[cur]);
addedge(cur, ls[cur], 0); addedge(cur, rs[cur], 0);
}
void build_o(int L, int R, int &cur) {
cur = ++ttot;
addedge(cur - tcnt, cur, 0);
if (L == R) return o_p[L] = cur, h[cur] = a[L], isg[cur] = a[L] > 0, void();
int mid = (L + R) >> 1;
build_o(L, mid, ls[cur]), build_o(mid + 1, R, rs[cur]);
addedge(ls[cur], cur, 0), addedge(rs[cur], cur, 0);
}
P5025 [SNOI2017]炸弹
题意:求一维坐标上炸弹引爆个数
实际上要求的是有向图上的某点出发能经过的点的权值和。
需要单点向区间点连边。因此需要线段树优化建图。
缩点后跑dp 这样会算重,但是洛谷数据太毒了,bzoj这样可以AC,洛谷86pts
由于最终答案一定为一段连续的闭区间,因此可以记录mx和mn,然后dfs+记搜。
然后就56pts了
好像这里建两棵树要WA,看来有的时候建一棵树要更好一些。(只有单点连向多点的时候)
弹跳
这个比较例外。这个题利用K-D Tree空间消耗小的优点,实现单点对矩形的最短路优化建图。
这也提示我们可以灵活运用各种数据结构来优化建图。只要方法合法,且包含所有合法情况,就可以考虑去这么写。
Ants
这个是线段树优化建图跑 2-SAT,需要用到前缀优化建2-SAT的思想。
前缀优化建图通常解决的问题是,一个集合中如果选了其中一个点,那么其余点都不能选。它大概长这个样子:
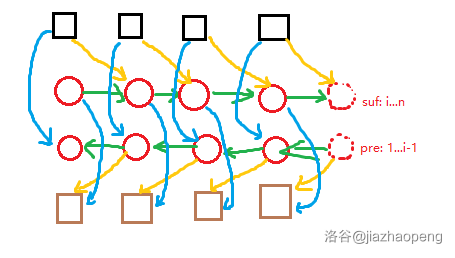
其中两排红点为辅助点,分别表示后缀点和前缀点。黑、棕色方点为原始节点。
线段树优化建图的问题则是,一个线段树节点内存着若干个点,如果选了其中一个点,那么其余点都不能选,且线段树的祖先节点内的点和子树内的点也不能被选。它大概长这个样子:
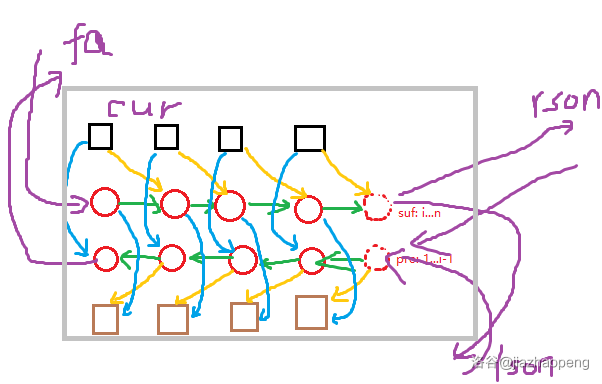
大概就是把父子的串给连起来。
需要注意的是,这种方法的节点数特别多,点数和边数都是 (O(n log n)) 级别的。这道题是树剖套线段树,所以是 (O(n log^2 n)) 的。
Flags
这个是普通的线段树优化建图跑2-sat,新建的点和新建的边并不符合对称性,只不过与朴素建图等价。
附
模板:单源最短路(调试用)
void build(int L, int R, int &cur) {
cur = ++ttot;
if (L == R) return ;
int mid = (L + R) >> 1;
build(L, mid, ls[cur]), build(mid + 1, R, rs[cur]);
if (type) addedge(cur, ls[cur], 0), addedge(cur, rs[cur], 0);
else addedge(ls[cur], cur, 0), addedge(rs[cur], cur, 0);
}
int ptot;
void Out(int L, int R, int l, int r, int p, int w, int cur) {
if (l <= L && R <= r) {
addedge(cur, p, 0);
return ;
}
int mid = (L + R) >> 1;
if (l <= mid) Out(L, mid, l, r, p, w, ls[cur]);
if (r > mid) Out(mid + 1, R, l, r, p, w, rs[cur]);
}
void In(int L, int R, int l, int r, int p, int w, int cur) {
if (l <= L && R <= r) {
addedge(p, cur, w);
return ;
}
int mid = (L + R) >> 1;
if (l <= mid) In(L, mid, l, r, p, w, ls[cur]);
if (r > mid) In(mid + 1, R, l, r, p, w, rs[cur]);
}
inline void Link(int l, int r, int l_, int r_, int w) {
++ptot;
Out(1, n, l, r, ptot, w, root_o);
In(1, n, l_, r_, ptot, w, root_i);
}
int find(int L, int R, int pos, int cur) {
if (L == R) return cur;
int mid = (L + R) >> 1;
if (pos <= mid) return find(L, mid, pos, ls[cur]);
return find(mid + 1, R, pos, rs[cur]);
}
struct node{
int cur;
ll val;
bool operator <(const node a) const {
return val > a.val;
}
};
priority_queue<node> q;
ll dis[N];
bool vis[N];
inline void dij() {
int st = find(1, n, s, root_i);
memset(dis, 0x3f, sizeof(dis));
q.push((node){st, 0}); dis[st] = 0;
while (!q.empty()) {
int cur = q.top().cur; q.pop();
if (vis[cur]) continue;
vis[cur] = true;
for (register int i = head[cur]; i; i = e[i].nxt) {
int to =e[i].to;
if (dis[to] > dis[cur] + e[i].val) {
dis[to] = dis[cur] + e[i].val;
q.push((node){to, dis[to]});
}
}
}
}
void print(int L, int R, int cur) {
if (L == R) {
printf("%lld ", dis[cur] >= inf ? -1ll : dis[cur]);
return ;
}
int mid = (L + R) >> 1;
print(L, mid, ls[cur]);
print(mid + 1, R, rs[cur]);
}
int main() {
read(n), read(m), read(s);
type = 1, build(1, n, root_i); int tot = ttot;
type = 0, build(1, n, root_o);
for (register int i = 1; i <= tot; ++i)
addedge(i, i + tot, 0);
ptot = ttot;
for (...) Link(l, r, l_, r_);
dij();
print(1, n, root_i);
puts("");
return 0;
}