0x00 概述
AdaBoost,全称是“Adaptive Boosting”,由Freund和Schapire在1995年首次提出,并在1996发布了一篇新的论文证明其在实际数据集中的效果。
这篇博客主要解释AdaBoost的算法详情以及实现。它可以理解为是首个“boosting”方式的集成算法。是一个关注二分类的集成算法。
0x01 算法的总体情况
AdaBoost的目标是建立如下的最终的分类器:

其中,假设我们输入的训练数据总共有nn个,用(x_1,y_y),cdots,(x_n,y_n)(x1,yy),⋯,(xn,yn)表示,其中xx是一个多为向量,而其对应的y={-1,1}y={−1,1}。
1.1 sign函数
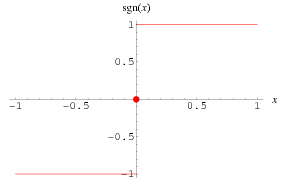
这里的signsign函数是符号函数。
判断实数的正负号。即如果输入是正数,那么输出为1;输入为负数,那么输出为-1;如果输入是0的话,那么输出为0。因此,AdaBoost的目标是判断{-1,1}{−1,1}的二分类判别算法。其函数图像如下所示:
1.2 弱分类器f(x)
模型中的f_m(x)fm(x)是弱分类器。
这里假设一个AdaBoost是由MM个弱分类器加全求和得到。每一个弱分类器f_m(x)fm(x)都给出一个预测结果,然后根据其对应的权重 heta_mθm加权求和。因此,我们可以看到,AdaBoost的目标其实就是求出每个弱分类器的模型参数,以及其对应的权重。
0x02 AdaBoost的求解
前面可以看到AdaBoost的模型本身非常简单。那么,如何求解这个模型中弱分类器的权重及其参数呢?其步骤如下:
首先,根据前面所述,有nn个数据,我们初始化每个数据的权重都是一样的:
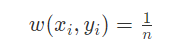
接下来,我们对每一个弱分类器(1,cdots,M)(1,⋯,M)都进行如下操作:
1) 训练一个弱分类器,使得其分类误差最小,此时计算该分类器的误差计算如下公式:
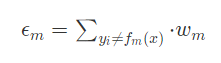
这个公式的含义就是模型的误差等于每一个错分的样本权重之和。
当该模型是第一个弱分类器(即第一次迭代的时候),该公式中的含义就是计算当前弱分类器分错的样本个数,除以总的样本数量,得到该弱分类器的误差(因为,此时每个样本的误差都是1/n)。同时注意,在后面的迭代中,每个错分的样本的权重是不同的,这里的mm表示第mm次迭代时候,该样本的权重。
2)根据当前弱分类器的误差,计算该分类器的权重:
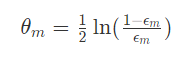
该公式的含义就是,当该弱分类器的准确率(1-前面的误差)大于0.5,那么这个权重就是正值(因为此时epsilon_m< 0.5ϵm<0.5,那么对数内部就是大于1,那么结果就是正数了)。否则该权重为负值。也就是说,只要这个分类器的准确率结果不是0.5(这个时候就相当于随机猜测了),它总会给最终的分类器提供一些信息。
3)最后,我们根据模型权重更新数据的权重:
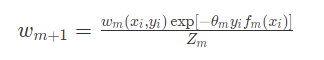
这里的Z_mZm是正规化系数,确保所有的数据权重总和为1。
解释一下这个公式的含义,指数内部- heta_my_if_m(x_i)−θmyifm(xi)这个乘积的含义是如果弱分类器mm的分类结果和真实的结果一致,那么结果是- heta_m−θm,是一个负值,那么exp[- heta_my_if_m(x_i)]exp[−θmyifm(xi)]结果小于1。也就是说该数据集的样本权重降低。否则该数据样本的权重增高。因此,通过这种计算就可以让那些容易分错的样本的权重升高,容易分对的样本权重降低。继续迭代就会导致对难分的样本能分对的模型的权重上涨。最终,达到一个强分类器的目的。
0x03 AdaBoost的Python实现
根据上述原理,AdaBoost的实现就很容易了。这里的主要目标是训练好每个弱分类器的同时,计算好分类器的权重。
# 载入数据 # 训练数据的特征和标签 x_train, y_train = ... # 预测数据的特征 y_train = ... # 定义分类器数量 M = 100 models = getModel(100) # 计算数据数量 n_train = x_train.shape[0] # 初始化数据权重 w = np.ones(n_train) / n_train # 初始化模型权重 theta = np.zeros(n_train) # 循环迭代 for m in range(M): # 训练一个弱分类器 models[m].fit(x_train,y_train) # 计算弱分类器误差 pred_train = models[m].predict(x_train) miss = [int(x) for x in (pred_train != y_train)] error = np.dot(w, miss) # 计算弱分类器的权重 theta[m] = 0.5 * np.log((1-error)/error) # 更新数据权重 for i in n_train: w[i] = w[i]*np.exp(-theta[m]*y_train[i]*pred_train[i]) # 正规化权重 for i in n_train: w[i] /= np.sum(w[i]) # 最终的预测 predict = np.dot(theta, [model[m].predict(x_test) for m in range(M)])