【问题描述】
0-1背包问题:有 N 个物品,物品 i 的重量为整数 wi >=0,价值为整数 vi >=0,背包所能承受的最大重量为整数 C。如果限定每种物品只能选择0个或1个,求可装的最大价值。
可以用公式表示为:
 【算法思路】
【算法思路】
动态规划法。我们可以想到这个问题具有最优子结构性质,假设(x1,x2,...,xn)是最优解,那么在去除x1之后,剩下(x2,...,xn)肯定是以下问题的最优解:

根据这个特征可以设计DP函数并推出递归关系。具体地,m(i,j)是背包容量为j,可选择物品为i,i+1,…,n时0-1背包问题的最优值。由0-1背包问题的最优子结构性质,则:
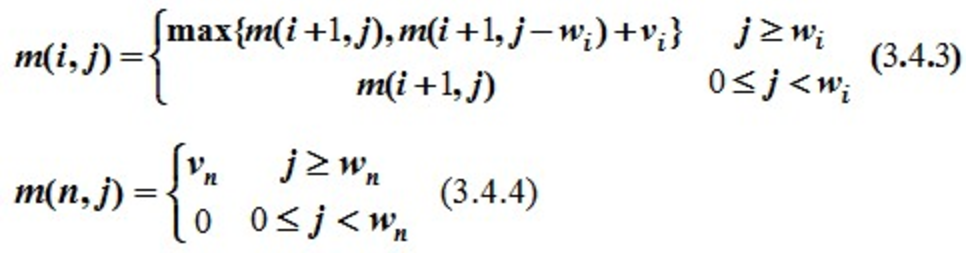
按着DP[N][C]的矩阵一个一个从 下 往 上 填就可以了,最后的结果是 DP(1,C)。要输出选取的样本编号的时候可以从前往后, DP(1,C)== DP(2,C),则x1=0,否则1,依次类推即可。
【代码】
1 #include<iostream> 2 #include<algorithm> 3 #include <stdio.h> 4 #define MAXN 10000 5 using namespace std; 6 7 int W[MAXN]; 8 int V[MAXN]; 9 int DP[MAXN][MAXN]= {0}; 10 11 int knapsack(int C, int N, int W[], int V[], int DP[][MAXN]) 12 { 13 int lackL = min(C, W[N]-1); 14 for(int j = 0; j <=lackL; j++) DP[N][j] = 0; 15 for(int j = W[N]; j <=C; j++) DP[N][j] = V[N]; 16 for(int i = N - 1; i>=1; i--){ 17 lackL = min(C, W[i]-1); 18 for(int j = 0; j <=lackL; j++) DP[i][j] = DP[i+1][j]; 19 for(int j = W[i]; j <=C; j++){ 20 DP[i][j] = max( DP[i+1][j], DP[i+1][j-W[i]] + V[i] ); 21 } 22 } 23 return DP[1][C]; 24 } 25 26 int main() 27 { 28 int C, N; 29 cin >> C >> N; 30 for(int i = 1; i <=N; i++) { 31 cin >> W[i] >> V[i]; 32 } 33 cout<<knapsack(C, N, W, V, DP)<<endl; 34 35 return 0; 36 }
【拓展】
如果现在的物品重量weight和背包容量C都是正整数,那么当他们是实数时,如何改进算法满足问题呢?
待完善(算法设计与分析P73)