题目描述:
风见幽香非常喜欢玩一个叫做 osu! 的游戏,其中她最喜欢玩的模式就是接水果。由于她已经 DT FC 了 The big black,她觉得这个游戏太简单了,于是发明了一个更加难的版本。
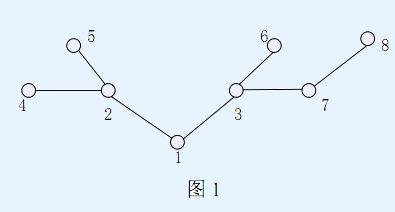
首先有一个地图,是一棵由 $n$ 个顶点、$n-1$ 条边组成的树(例如图 $1$ 给出的树包含 $8$ 个顶点、$7$ 条边)。这颗树上有 P 个盘子,每个盘子实际上是一条路径(例如图 $1$ 中顶点 $6$ 到顶点 $8$ 的路径),并且每个盘子还有一个权值。第 $i$ 个盘子就是顶点 $a_i$ 到顶点 $b_i$ 的路径(由于是树,所以从 $a_i$ 到 $b_i$ 的路径是唯一的),权值为 $c_i$。接下来依次会有 $Q$ 个水果掉下来,每个水果本质上也是一条路径,第 $i$ 个水果是从顶点 $u_i$ 到顶点 $v_i$ 的路径。
幽香每次需要选择一个盘子去接当前的水果:一个盘子能接住一个水果,当且仅当盘子的路径是水果的路径的子路径(例如图 $1$ 中从 $3$ 到 $7$ 的路径是从 $1$ 到 $8$ 的路径的子路径)。这里规定:从 $a$ 到 $b$ 的路径与从 $b$ 到 $a$ 的路径是同一条路径。当然为了提高难度,对于第 $i$ 个水果,你需要选择能接住它的所有盘子中,权值第 $k_i$ 小的那个盘子,每个盘子可重复使用(没有使用次数的上限:一个盘子接完一个水果后,后面还可继续接其他水果,只要它是水果路径的子路径)。幽香认为这个游戏很难,你能轻松解决给她看吗?
输入:
第一行三个数 $n$ 和 $P$ 和 $Q$,表示树的大小和盘子的个数和水果的个数。
接下来 $n-1$ 行,每行两个数 $a$、$b$,表示树上的 $a$ 和 $b$ 之间有一条边。树中顶点按 $1$ 到 $n$ 标号。 接下来 $P$ 行,每行三个数 $a$、$b$、$c$,表示路径为 $a$ 到 $b$、权值为 $c$ 的盘子,其中 $0 leq c leq 10^9, a
eq b$。
接下来 $Q$ 行,每行三个数 $u$、$v$、$k$,表示路径为 $u$ 到 $v$ 的水果,其中 $u$ 不等于 $v$,你需要选择第 $k$ 小的盘子,第 $k$ 小一定存在。
输出:
对于每个果子,输出一行表示选择的盘子的权值。
数据范围:
对于所有数据,$N,P,Q leq 40000$。
算法标签:整体二分,树状数组,扫描线
思路:
考虑对于一个盘子两端为 $a,b$ ,如果两点的 $lca$ 不在路径的端点上,那么当水果的两端$x,y$的范围为
$dfn[a]le dfn[x]le end[a]$ && $dfn[b]le dfn[y]le end[b]$
时这个盘子的路径是水果的子路径。
如果lca在端点上,不妨令 $a$ 为深度小的点,那么我们倍增找到在 $a,b$ 路径上为 $b$ 的祖先, $a$ 的儿子的那个点 $w$ ,那么水果的两端 $x,y$ 的范围为
$ (1le dfn[x]le dfn[w]-1$ && $dfn[b]le dfn[y]le end[b] ) || ( dfn[b]le dfn[x]le end[b]$ & $end[w]+1le dfn[y]le n)$
时这个盘子的路径是水果的子路径。
盘子其实是一个矩形或者两个矩形。
所以我们可以将询问排序,进行整体二分,两维限制条件一维用树状数组维护,一维扫描线维护
以下代码:

#include<bits/stdc++.h> #define il inline #define _(d) while(d(isdigit(ch=getchar()))) using namespace std; const int N=8e4+5; int dfn[N],ed[N],id,fa[N][20],d[N],ans[N]; int n,p,q,head[N],ne[N],to[N],cnt,tot,sum[N],g[N]; struct node{int l1,r1,l2,r2,v;}t[N]; struct data{int x,y,k,id;}poi[N],tmp1[N],tmp2[N]; struct kk{int x,l2,r2,v,id;}e[N<<1]; il int read(){ int x,f=1;char ch; _(!)ch=='-'?f=-1:f;x=ch^48; _()x=(x<<1)+(x<<3)+(ch^48); return f*x; } bool cmp(node t1,node t2){return t1.v<t2.v;} bool cmp1(kk t1,kk t2){ return (t1.x<t2.x||(t1.x==t2.x&&t1.id<t2.id)); } il void ins(int x,int y){ ne[++cnt]=head[x]; head[x]=cnt;to[cnt]=y; } il void dfs(int x){ dfn[x]=++id; for(int i=1;fa[x][i-1];i++)fa[x][i]=fa[fa[x][i-1]][i-1]; for(int i=head[x];i;i=ne[i]){ if(fa[x][0]==to[i])continue; fa[to[i]][0]=x; d[to[i]]=d[x]+1;dfs(to[i]); } ed[x]=id; } il int LCA(int x,int y){ if(d[x]<d[y])swap(x,y); for(int i=18;i>=0;i--)if(d[fa[x][i]]>=d[y])x=fa[x][i]; if(x==y)return x; for(int i=18;i>=0;i--)if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i]; return fa[x][0]; } il int jump(int x,int y){ for(int i=18;i>=0;i--)if(d[fa[x][i]]>d[y])x=fa[x][i]; return x; } il int query(int x){ int ans=0; for(;x;x-=x&-x)ans+=g[x]; return ans; } il void insert(int l,int r,int v){ r++; for(;r<=n;r+=r&-r)g[r]-=v; for(;l<=n;l+=l&-l)g[l]+=v; } il void solve(int l,int r,int ql,int qr){ if(ql>qr)return; if(l==r){ for(int i=ql;i<=qr;i++)ans[poi[i].id]=t[l].v; return; } int mid=(l+r)>>1,sz=0; for(int i=l;i<=mid;i++){ e[++sz]=(kk){t[i].l1,t[i].l2,t[i].r2,1,0}; e[++sz]=(kk){t[i].r1,t[i].l2,t[i].r2,-1,n+1}; } for(int i=ql;i<=qr;i++) e[++sz]=(kk){poi[i].x,poi[i].y,0,0,i}; sort(e+1,e+1+sz,cmp1); for(int i=1;i<=sz;i++){ if(ql<=e[i].id&&e[i].id<=qr)sum[e[i].id]=query(e[i].l2); else insert(e[i].l2,e[i].r2,e[i].v); } for(int i=1;i<=sz;i++)if(e[i].id==0||e[i].id==n+1)insert(e[i].l2,e[i].r2,-e[i].v); int a=0,b=0; for(int i=ql;i<=qr;i++){ if(sum[i]>=poi[i].k)tmp1[++a]=poi[i]; else tmp2[++b]=(data){poi[i].x,poi[i].y,poi[i].k-sum[i],poi[i].id}; } for(int i=ql;i<=ql+a-1;i++)poi[i]=tmp1[i-ql+1]; for(int i=ql+a;i<=qr;i++)poi[i]=tmp2[i-ql-a+1]; solve(l,mid,ql,ql+a-1);solve(mid+1,r,ql+a,qr); } int main() { n=read();p=read();q=read(); for(int i=1;i<n;i++){ int x=read(),y=read(); ins(x,y);ins(y,x); } d[1]=1;dfs(1); for(int i=1;i<=p;i++){ int a=read(),b=read(),c=read(); int lca=LCA(a,b);if(dfn[a]>dfn[b])swap(a,b); if(lca!=a){ t[++tot]=(node){dfn[a],ed[a],dfn[b],ed[b],c}; } else{ int w=jump(b,a); t[++tot]=(node){1,dfn[w]-1,dfn[b],ed[b],c}; if(ed[w]<n)t[++tot]=(node){dfn[b],ed[b],ed[w]+1,n,c}; } } sort(t+1,t+1+tot,cmp); for(int i=1;i<=q;i++){ int x=read(),y=read(),k=read(); if(dfn[x]>dfn[y])swap(x,y); poi[i]=(data){dfn[x],dfn[y],k,i}; } solve(1,tot,1,q); for(int i=1;i<=q;i++)printf("%d ",ans[i]); return 0; }
