2-SAT

推荐blog：

https://www.mina.moe/archives/11387

https://www.cnblogs.com/cjjsb/p/9771868.html

SAT是适定性(Satisfiability)问题的简称 。一般形式为k-适定性问题，简称 k-SAT

可以证明，当k>2时，k-SAT是NP完全的。因此一般讨论的是k==2的情况，即2-SAT问题。

2-SAT用处 ：有若干个包含2个元素的集合，只能选择每个集合中的一个元素，并给出一些条件（例：选a后不能选b），要求求出满足这些条件的选择，这个解也称为2-SAT的解

如何求解？

如上图，为{A,A'},{B,B'},{C,C'}这几个集合

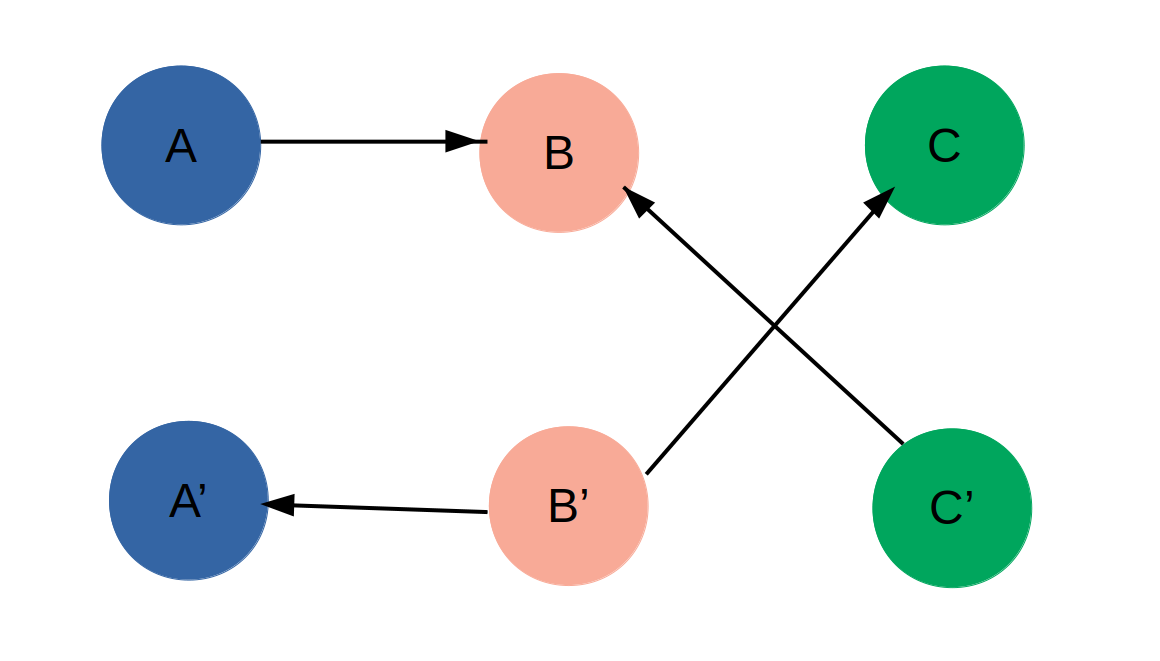
若给出条件，{A,B'},{B‘C’}不能同时选择

因为{A,A'},{B,B'},{C,C'}中，每个集合都要选出一个元素，即不能同时选择

又因为{A,B'}不能同时选择，则选择B‘时，一定选择A’，于是在B‘，A’之间连上一条有向边（因为选A‘不一定B’）；同理，在选B时也一定选A

其它也同上处理，于是：

接着再进行缩点，然而这个栗子中没有可缩的点，判断对称的两点是否在同一个强连通分量中，若在，则无解

若不在，我们接着应该求出符合要求的解，如何求呢

1.进行拓扑排序（不用了）我们可以发现，缩点后强连通分量的编号就是反着的拓扑排序

为什么要拓扑排序呢？比如一个样例，它让A->B->A'，显然我们不能选A，只能选A’（拓扑排序大的），即选强连通分量编号小的

2.对于每一个集合，选出强连通分量小的

那为什么选小的一定能满足之前上面所有的条件呢？

可以这样想：

一个点如果被选了，那么选它而必须选的点，因为连了边，

所以，在遍历此点时也会将其他必须选的点赋上颜色，

然而下一次，从另一个点开始遍历时，选这个点而会被选上的点，又会被赋值

然而这一次被赋上的值的点 的值，一定比上一次赋上值的点 的值 要大

所以挑最小的一定能满足所有的条件

推荐题：luogu P4782

#include<bits/stdc++.h>
using namespace std;
int head[2000006],zhan[2000006],color[2000006],dfn[2000006],low[2000005];
int num,Color,dfx,top;
bool pd[2000005];
struct{
    int to,next;
}a[2000006];
void lian(int from,int to){
    num++;
    a[num].to=to;
    a[num].next=head[from];
    head[from]=num;
}
void tarjan(int x){
    int i;
    dfn[x]=low[x]=++dfx;zhan[++top]=x;
    pd[x]=1;
    for(i=head[x];i;i=a[i].next){
        if(pd[a[i].to]==0){
            tarjan(a[i].to);
            low[x]=min(low[x],low[a[i].to]);
        }
        if(color[a[i].to]==0)low[x]=min(low[x],dfn[a[i].to]);
    }
    if(low[x]==dfn[x]){
        Color++;
        do{
            i=zhan[top];top--;            
            color[i]=Color;
        }while(low[i]!=dfn[i]);
    }
}
int main(){
    int n,m,i,j,a,_a,b,_b;
    scanf("%d%d",&n,&m);
    for(i=1;i<=m;i++){
        scanf("%d%d%d%d",&a,&_a,&b,&_b);
        if(_a==0&&_b==0)lian(a+n,b),lian(b+n,a);
        else if(_a==1&&_b==0)lian(a,b),lian(b+n,a+n);
        else if(_a==0&&_b==1)lian(a+n,b+n),lian(b,a);
        else lian(a,b+n),lian(b,a+n);
    }
    for(i=1;i<=2*n;i++){
        if(color[i]==0)tarjan(i);
    }
    for(i=1;i<=n;i++){
        if(color[i]==color[i+n]){
            printf("IMPOSSIBLE
");
            return 0;
        }
    }
    printf("POSSIBLE
");    
    for(i=1;i<=n;i++){
        if(color[i]<color[i+n])printf("0 ");
        else printf("1 ");
    }
    return 0;
}