11. Container With Most Water[M]盛最多水的容器

题目

Given (n) non-negative integers (a_1,a_2,cdots,a_n), where each represents a point at coordinate((i,a_i))，(n) vetical lines are drawn such that the two endpoints of line (i) is at ((i,a_i)) and ((i,0)). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and (n) is at least 2.

#思路

---

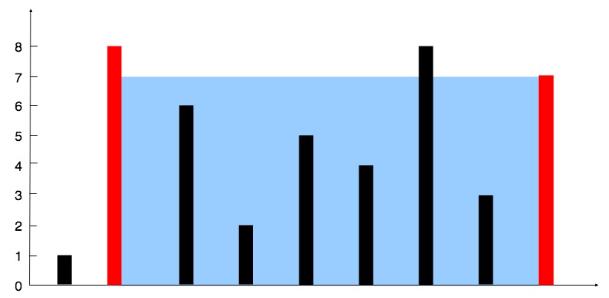
思路1：暴力匹配法

考虑到每一种出现的线段组合，并求出这些组合下的最大面积。

思路2：双指针法

两线段的距离越远，面积越大；同时，线段之间形成的容器区域受到长度较短的那条的线段限制。
在数组中使用双指针，一个指向数组的开头，一个指向末尾。计算线段形成的区域面积，并用(max)存储目前为止获得的最大区域的面积。此外，指针的移动方向是，较短线段的指针向较长线段的指针移动。
由于矩形容器的面积受限于较短长度的线段，当较长线段的指针向较短线段移动时，矩形面积不会增加。但是，当移动较短线段的指针虽然会影响矩形的宽度的减小，但是由于移动的方向是将较短线段的指针向较长线段的指针移动，矩形会获得更大的高度，这可能会导致面积的增加

Tips

---

双指针法

利用两个指针来遍历数组，一般来说，遍历数组采用的是单指针。两个指针一般用于有序数组，利用两个相同方向或者相反方向的指针完成遍历。（这里的指针并非C中的指针，而是指数组索引）

C++

---

• 思路1

class Solution {
public:
    int maxArea(vector<int>$ height){
        int max = 0;
        for(int i = 0; i< height.size(); i++){
            for(int j = 0; j< height.size(); j++){
                int wide = height[i] > height[j] ? height[j] : height[i];   
                int len = j - i;   
                int temMax = len * wide;      
                if(tempMax > max)        
                    max = tempMax;    
            }  
        }
        return max;
    }
};

• 思路2

class Solution {
public:
    int maxArea(vector<int>& height){
  
        int pBegin = 0; //开始指针
        int pEnd = height.size() - 1; //末尾指针
        int max = 0;
        
        while(pBegin < pEnd){
            int minHeight = height[pBegin] < height[pEnd] ? height[pBegin] : height[pEnd]; 
            int tempMax = minHeight * (pEnd - pBegin);
            
            if (tempMax > max)
                max = tempMax;
            if (height[pBegin] < height[pEnd]){
                pBegin ++;
            } 
            else{
 
                pEnd --; 
            }
        }
        return max;

    }
};

Python

---

• 思路2

 def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        pBegin = 0
        pEnd = len(height) - 1
        resInt = 0
        while pBegin < pEnd:
            curArea = (pEnd - pBegin) *min(height[pBegin], height[pEnd])
            if curArea > resInt:
                resInt = curArea
            if height[pBegin] < height[pEnd]:
                pBegin += 1
            else:
                pEnd -= 1
        return resInt