本组囊括二叉树中匹配类问题。
对于二叉树的题目,无非就以下几种解题思路:
先序遍历(深度优先搜索);
中序遍历(深度优先搜索)(尤其二叉搜索树);
后序遍历(深度优先搜索);
层序遍历(广度优先搜索)(尤其按照层来解决问题的时候);
序列化与反序列化(结构唯一性问题),如剑指offer 37;
匹配类问题;
本组介绍最后一类匹配类问题,匹配类二叉树可以使用一种套路相对固定的递归函数,在周赛中和每日一题中多次出现,而第一次见到不太容易写出正确的递归解法,因此这里来总结一下。
这类题目与字符串匹配有些神似,求解过程大致分为两步:
先将根节点匹配;
根节点匹配后,对子树进行匹配。
而参与匹配的二叉树可以是一棵,与自身匹配;也可以是两棵,即互相匹配。
比如「101. 对称二叉树」就是两棵树之间的匹配问题。为了更具一般性,我们先来看「面试题 04.10. 检查子树」这道题。
面试题 04.10. 检查子树
难度:中等

思路:
匹配类典型题目,此题归于自身匹配问题,使用一个递归函数dfs;
此题思路为:先判断t的根节点是否是s的节点之一,在确定根节点的情况下使用递归函数dfs去匹配二叉树;
确定根节点为C后,判断t树是否是C树的子树。
解法:
1 class Solution: 2 def checkSubTree(self, s: TreeNode, t: TreeNode) -> bool: 3 # 匹配类典型题目,此题归于自身匹配问题,使用一个递归函数dfs 4 # 此题思路为:先判断t的根节点是否是s的节点之一,在确定根节点的情况下使用递归函数dfs去匹配二叉树 5 # 确定根节点为C后,判断t树是否是C树的子树 6 7 # 先写dfs函数 8 def dfs(s, t): 9 if not s and not t: # 两棵树都到达空节点,说明完全匹配 10 return True 11 if not s or not t: # 两棵树有一颗先到达了空节点,说明不完全匹配,按照题意这种的所有类型都不属于子树 12 return False 13 # 其他情况放进return内考虑 14 return s.val == t.val and dfs(s.left, t.left) and dfs(s.right, t.right) 15 16 # 再写主函数,宏观上来看,主函数就是先去匹配根,在匹配到根节点的情况下,去执行递归函数dfs,相当于双重递归。 17 # 这里用一种统一的模板来写主函数,可用于这些两棵树匹配的题目: 18 if not t or not s: # 19 return False 20 21 if dfs(s, t): # 目前传入的两棵树满足匹配条件,直接返回 22 return True 23 # 否则继续遍历s树的根,去一一和t树匹配,只要匹配到一个点即可返回真 24 return self.checkSubTree(s.left, t) or self.checkSubTree(s.right, t)
剑指 Offer 26. 树的子结构
难度:中等
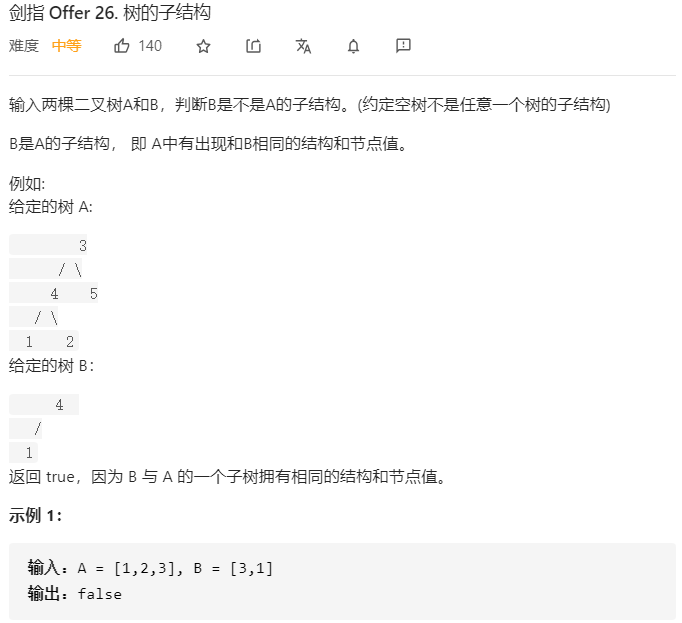
思路:这题和上题的区别即为B可不用到达A的叶子节点
先将根节点匹配,于是主函数的目的就是找到A树中根节点和B根节点值相同的节点,然后开始调用辅助函数去递归判断子树结构是否匹配。
辅助函数dfs作用即为确定了A B 根节点后,同时往下递归匹配,由于题目只要求B是A的一部分,不一定走到叶子节点,所以B走到叶子节点后就可以返回True,如果A先走到了叶子节点说明不匹配,返回False,当然递归还要判断A/B当前节点值是否相等,这些可以放到返回值中。
这样我们可以定下函数dfs的输入输出和作用:
输入:根节点A,根节点B
返回值: ture/false, 当继续遍历时继续递归当前值是否相等and A/B的左右子树匹配。
将视野放远来看,主函数则解决了如何确定 A 的哪个节点是 B 的根节点。
如果 A 的当前节点值与 B 的根节点值相同,我们调用 dfs 函数判断子树是否也相同;如果不同,我们就递归调用主函数来寻找 A 的哪个节点与 B 的根节点匹配。
解法:
1 class Solution: 2 def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool: 3 # 大神总结:递归 深度优先搜索 4 # 匹配类二叉树可以使用一种套路相对固定的递归函数,在周赛中和每日一题中多次出现,而第一次见到不太容易写出正确的递归解法,因此我们来总结一下。(注:不要太纠结于名字,因为名字是我自己起的......) 5 # 这类题目与字符串匹配有些神似,求解过程大致分为两步: 6 # 先将根节点匹配; 7 # 根节点匹配后,对子树进行匹配。 8 # 而参与匹配的二叉树可以是一棵,与自身匹配;也可以是两棵,即互相匹配。 9 # 比如「101. 对称二叉树」就是两棵子树之间的匹配问题。为了更具一般性,我们先来看「面试题 04.10. 检查子树」这道题。 10 11 # 思路一: 12 # 1.先将根节点匹配,于是主函数的目的就是找到A树中根节点和B根节点值相同的节点,然后开始调用辅助函数去递归判断子树结构是否匹配。 13 # 辅助函数dfs作用即为确定了A B 根节点后,同时往下递归匹配,由于题目只要求B是A的一部分,不一定走到叶子节点,所以B走到叶子节点后就可以返回True,如果A先走到了叶子节点说明不匹配,返回False,当然递归还要判断A/B当前节点值是否相等,这些可以放到返回值中。 14 # 这样我们可以定下函数dfs的输入输出和作用: 15 # 输入:根节点A,根节点B 16 # 返回值: ture/false, 当继续遍历时继续递归当前值是否相等and A/B的左右子树匹配 17 # 将视野放远来看,主函数则解决了如何确定 A 的哪个节点是 B 的根节点。 18 # 如果 A 的当前节点值与 B 的根节点值相同,我们调用 dfs 函数判断子树是否也相同;如果不同,我们就递归调用主函数来寻找 A 的哪个节点与 B 的根节点匹配。 19 def dfs(root1, root2): # root1为主树 20 if not root2: # 两个一起遍历下来,都匹配,然后B树空了,说明完全匹配了,这里是这道题的关键!! 只需要B树遍历为空就行,A树不管 21 return True 22 if not root1: # root1先到底了 23 return False 24 if root1.val != root2.val: 25 return False 26 return dfs(root1.left, root2.left) and dfs(root1.right, root2.right) 27 28 # 来看主函数 29 if not A or not B: 30 return False # 如果A或B本身为空,根据题意,肯定不匹配了 31 if dfs(A, B): # 目前传入的两棵树满足匹配条件,直接返回 32 return True 33 # 否则继续遍历A树的根,去一一和B树匹配,只要匹配到一个点即可返回真 34 return self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B) 35 # 时间复杂度: O(M+N),遍历两棵树节点数 36 # 空间复杂度:O(M), 递归的栈最多深度为A的节点数,当A/B 退化为链表
100. 相同的树
难度:简单

思路:
此题和上题基本一样,不过更为简单,无需dfs函数,主函数逐一递归即可。
解法:
1 class Solution: 2 def isSameTree(self, p: TreeNode, q: TreeNode) -> bool: 3 # 标签:深度优先遍历,使用递归实现深度优先遍历 4 # 对于这题来说,也是二叉树的先序遍历(先根后左最后右) 5 # 方法一:递归解法,首先判断q、p是否都为None,不是的话再检测是否其中一个为None或是两个的值相等,都满足的话就继续判断p、q的左右子节点。 6 if not p and not q: # p,q均为None 7 return True 8 if not p or not q: # p、q其中一个为none 9 return False 10 if p.val != q.val: # 都不为None但值不相等的情况 11 return False 12 return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right) # 递归判断两个子节点 13 # 时间复杂度:O(N),其中 N 是树的结点数,因为每个结点都访问一次。 14 # 空间复杂度: 最优情况(完全平衡二叉树)时为O(log(N)),最坏情况下(完全不平衡二叉树)时为O(N),用于维护递归栈。 15 16 # 方法二: 17 # 迭代法,常用的使用队列使递归转迭代方法 18 # 创造一个单向队列,先将树压入 19 queue = [p, q] 20 while queue: # 队列为空循环终止 21 left = queue.pop(0) 22 right = queue.pop(0) 23 if not left and not right: 24 continue 25 if not left or not right: 26 return False 27 if left.val != right.val: 28 return False 29 queue.append(left.left) # 添加左节点的左儿子 30 queue.append(right.left) # 右节点的左儿子 31 queue.append(left.right) # 左节点的右儿子 32 queue.append(right.right) # 右节点的右儿子 33 return True
下面是一道和自身匹配的题目:
101. 对称二叉树
难度:简单
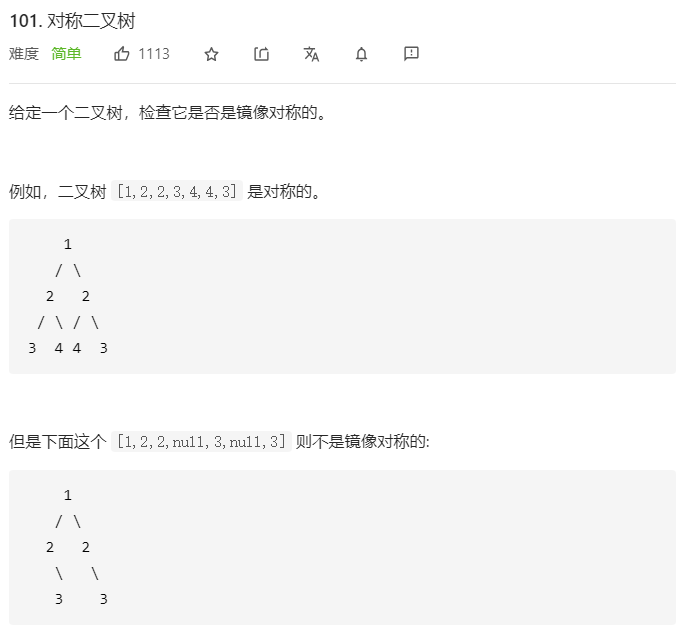
思路:
将自身看作两棵树,用左子树和右子树镜像比较;具体看注释。
解法:
1 class Solution: 2 def isSymmetric(self, root: TreeNode) -> bool: 3 # 解法一 4 # 递归 深度优先遍历/ 二叉树的先序遍历 5 # 在根节点值相等的情况下 递归地比较左子树的左节点和右子树的右节点,然后是左子树的右节点和右子树的左节点 6 # if not root: 7 # return True 8 # def dfs(left, right): 9 # if not left and not right:# 左子树和右子树均为空 10 # return True 11 # if not left or not right: # 左子树和右子树有一个为空 12 # return False 13 # if left.val != right.val: 14 # return False 15 # return dfs(left.left, right.right) and bfs(left.right, right.left) 16 # return dfs(root.left, root.right) 17 # 时间复杂度:O(N),N为树的节点数。 18 # 空间复杂度:最差O(N)。N为树的高度 19 20 # 解法二:迭代 21 # 树的迭代一般通过借助队列来完成:递归转迭代 22 # 首先我们把根节点的左右子节点加入队列,比较法则仍然是通递归一样,但如果左右均为空则循环继续 23 # 然后再在队列中添加左节点的左儿子,右节点的右儿子,左节点的右儿子,右节点的左儿子,依次比较 24 # 循环结束条件为队列为空或是我们判断出了不对称的情况 25 if not root or not (root.left or root.right): 26 return True 27 queue = [root.left, root.right] # 数组实现队列 28 while queue: # 队列非空 29 left = queue.pop(0) # 用pop(0)实现队列先入先出 30 right = queue.pop(0) 31 if not left and not right: 32 continue 33 if not left or not right: 34 return False 35 if left.val != right.val: 36 return False 37 queue.append(left.left) # 左节点的左孩子 38 queue.append(right.right) # 右节点的右孩子 39 queue.append(left.right) # 左节点的右孩子 40 queue.append(right.left) # 右节点的左孩子,这四个全部加入队列,循环每次只比较前两个节点值,找到不对称或是队列为空循环终止 41 return True 42 # 时间复杂度:O(N),N为树的节点数。 43 # 空间复杂度:O(N),维护最多N个节点的队列
再来看几道类似的匹配类题目:
110. 平衡二叉树
难度:简单

思路:
此题和上题基本一样,不同的是dfs函数需要判断高度,具体看注释
解法:
1 class Solution: 2 def height(self, root): 3 if not root: # 递归终止条件 4 return 0 5 else: 6 return max(self.height(root.left), self.height(root.right)) + 1 7 def isBalanced(self, root: TreeNode) -> bool: 8 # 模式:递归,深度优先搜索 9 # 做好一个节点应该做好的事 10 # 这里需要一个height方法,计算子树的高度 11 # 解法一: 自顶向下的递归,判断子树的绝对值小于等于1后继续往下判断 12 # 缺点:由于引入一个方法height,且在该方法中也用到了递归,整体也用了递归,所以复杂度有点爆表 13 14 if not root: 15 return True 16 if abs(self.height(root.left) - self.height(root.right)) > 1: 17 return False 18 return self.isBalanced(root.left) and self.isBalanced(root.right) 19 20 # 时间复杂度:O(NlogN): 最差情况下,isBalanced(root) 遍历树所有节点,占用O(N);判断每个节点的最大高度 height(root) 需要遍历各子树的所有节点,子树的节点数的复杂度为 O(logN). 21 # 空间复杂度O(N): 最差情况下(树退化为链表时),系统递归需要使用O(N) 的栈空间。
剑指 Offer 27. 二叉树的镜像
难度:简单

思路:
此题要求输出树的镜像,建一颗树,dfs生成即可
解法:
1 class Solution: 2 def mirrorTree(self, root: TreeNode) -> TreeNode: 3 # 有点像主站的对称二叉树 4 # 弄清楚逻辑,其实镜像就是根>右>左的顺序往下复制 5 # 思路一:递归,深度优先搜索 6 # 根据二叉树镜像的定义,考虑递归遍历(dfs)二叉树,交换每个节点的左 / 右子节点,即可生成二叉树的镜像。 7 # 注意,不用生成新的二叉树,交换原来树的左右节点即可 8 # DFS 9 if not root: # 深度到越过叶子节点 10 return None 11 temp = root.left # 用一个值先保存原来root的左孩子,因为下面会改变 12 root.left = self.mirrorTree(root.right) 13 root.right = self.mirrorTree(temp) 14 return root 15 # 时间复杂度:O(N) 16 # 空间复杂度: 树的高度,最坏O(n),最好O(logn) 17 18 # 思路二: 迭代,用队列,广度优先搜索