LeetCode:二叉树（四）

本组囊括二叉树中由求路径总和的相关题目，最后做一个小小扩展。

 

129. Sum Root to Leaf Numbers

题目描述:中等

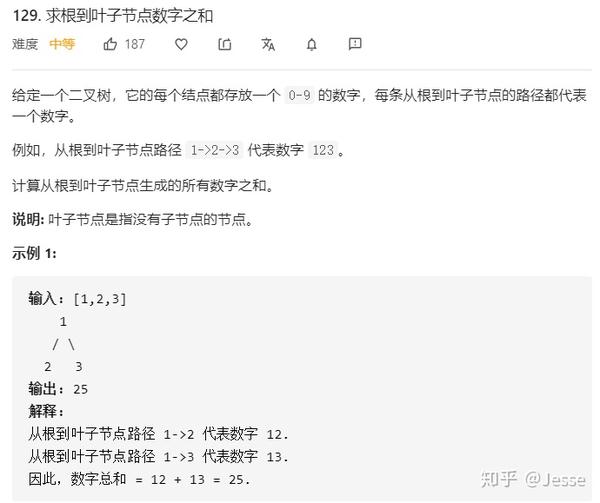
解法一：dfs

每层需要乘上10，递归实现，考虑dfs;
用一个sum来保存当前路径的和，用ans来保存当前所有路径的总和
每到一个子节点，sum = 子节点的值+sum*10作为当前路径，直到到达叶子节点，ans = ans+sum。

class Solution:
    def sumNumbers(self, root: TreeNode) -> int: 
        if not root:
            return 0
        def dfs(root, sum): # 递归函数，输入根节点和sum，输出无，不断更新ans
            sum = root.val + sum * 10
            if not root.left and not root.right:
                self.ans += sum
            if root.left:
                helper(root.left, sum)
            if root.right:
                helper(root.right, sum)   
        self.ans = 0 # 这样也可以定义一个全局变量,只是相对于内层函数dfs
        dfs(root, 0)
        return self.ans

 

112. Path Sum

题目描述:简单

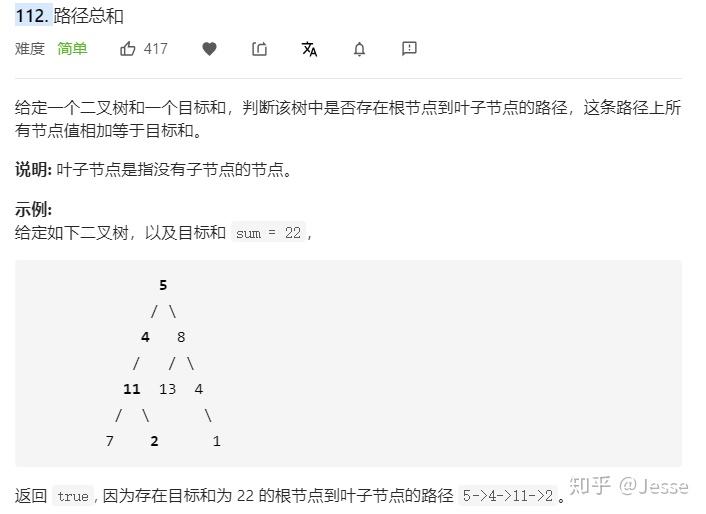
解法一：递归

遍历所有节点，让sum = sum - 该节点的值，然后再让该节点的孩子节点也调用hasPahSum函数，直到到达叶子节点，最后的sum如果为0，则说明找到了这样一条路径；

二叉树的递归是很有套路可循的，一般来说，当一个节点做完该做的事情后，其他就交给递归来做；
而树是左右分支的，所以最后一般递归时返回递归函数(left) (and/or) 递归函数(right)即可。

class Solution:
    def hasPathSum(self, root: TreeNode, sum: int) -> bool:
        if not root: # 空树
            return False
        sum -= root.val # 每步递归
        if root.left == None and root.right == None: # 递归结束条件
            return (sum == 0)
        return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum) # 只要有一条路径为True即可。
        # 时间复杂度：访问每个节点一次O(N)。
        # 空间复杂度：当树不平衡的最坏情况下是O(N)。在最好情况（树是平衡的）下是O(logN)。

 

113. Path Sum II

题目描述:中等

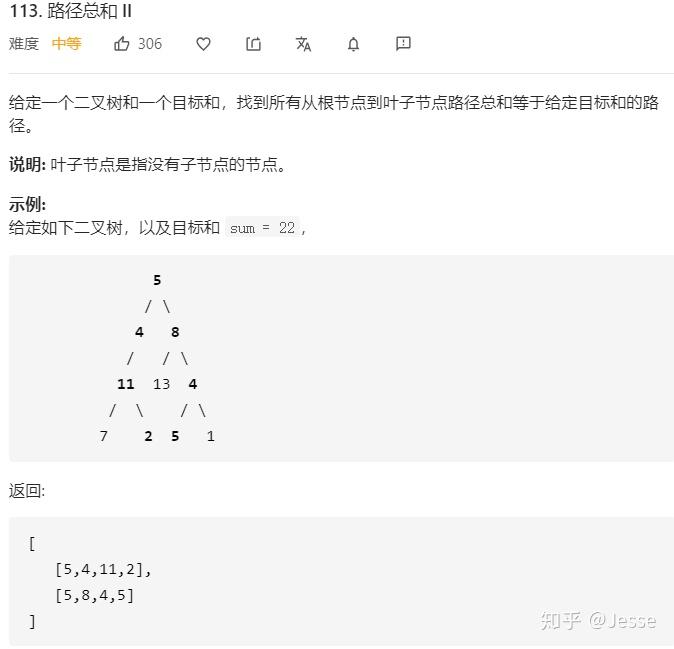
解法一：递归

这道题要求的路径是一定从根节点出发且要到达叶子节点，于是思路比较简单，采取dfs:

每次进入递归首先要自减当前的节点值,即sum -= root.val

递归终止条件，如果是叶子节点(not root.left and not root.right)，并且路径剩余和sum = 0了,把结果添加到结果数组；

如果存在左子树，递归左子树，右子树同理；

注意，数组在python中为可变类型，这里的path+[root.val]相当于从新创建了一个对象入栈，如果用append表示没有从新创建一个对象即原对象入栈，所以要错误。

class Solution(object):
    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: List[List[int]]
        ""
        if not root: return []
        ans = []
        path = []
        def dfs(root, path, sum):  
            sum -= root.val
            if sum == 0 and not root.left and not root.right: # 仅仅需要改这一行就行：
                ans.append(path + [root.val])
            if root.left:
                dfs(root.left, path+ [root.val], sum)
            if root.right:
                dfs(root.right, path + [root.val], sum)
        dfs(root, path, sum) # 想想把它传进去的第一个值的情况，就可以得出终止条件
        return ans

 

437. Path Sum III

题目描述:中等

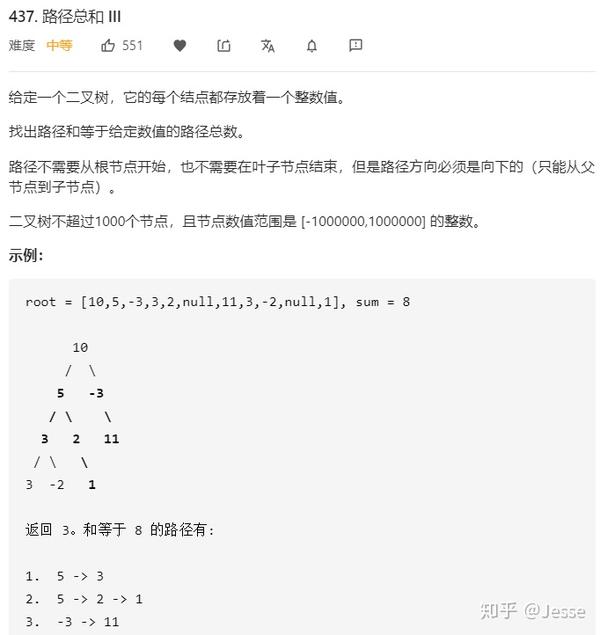
解法一：递归

这道题要求的路径是不一定从根节点出发且不一定要到达叶子节点，思路稍微变化一下即可：

首先依然是每次进入递归首先要自减当前的节点值,即sum -= root.val

递归终止条件，由于不需要到达叶子节点，所有只需要路径剩余和sum = 0了,方案数就+1；

如果存在左子树，递归左子树，右子树同理；

上面的递归函数为内层递归，其含义是从任一根节点开始寻找满足条件的路径，那当然我们也需要一个外层递归函数，这里即是我们的主函数pathSum,其含义是从某根节点为起点寻找路径，遍历完所有的根节点作为起点即可。

我们需要一个全局变量self.ans来记录结果。

class Solution(object):
    def __init__(self):
        self.ans = 0
    def pathSum(self, root, sum):
        # 递归，深度优先搜索
        # 情况3：不一定从根开始，也不一定从叶子结束
        # 先写写这种的方案数
        # 思路：双重递归
        # 其中外层递归应该是113题的以某点为起点找路径
        # 内层递归就是以各个点为起点.
        # 也可在此基础上实现具体的解。
        def dfs(root, sum): # 外层递归，以某点为起点找路径
            # if not root: # 结束条件
            #     return
            sum -= root.val
            if sum == 0:
                self.ans += 1
            if root.left:
                dfs(root.left, sum)
            if root.right:
                dfs(root.right, sum)
        # 主函数：
        # 主函数不应该每次置零self.res
        if not root:
            return self.ans
        dfs(root, sum)
        self.pathSum(root.left, sum)
        self.pathSum(root.right, sum)
        return self.ans

 

扩展

同样是类似的路径之和问题，如果我们固定根节点，路径定义为从根出发，不需要到达叶子节点即可呢，这样地去寻找具体有哪些路径。

解法一：递归

这道题要求的路径是一定从根节点出发但不一定要到达叶子节点，思路其实还是一样的，把递归的终止条件改变一下就行：

只需要路径剩余和sum = 0了,就把结果添加到结果数组；

如果存在左子树，递归左子树，右子树同理；

和上一题的区别就是，这题不需要外层递归函数了；

class Solution(object):
    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: List[List[int]]
        ""
        if not root: return []
        ans = []
        path = []
        def dfs(root, path, sum):  
            sum -= root.val
            if sum == 0: # 仅仅需要改这一行就行：
                ans.append(path + [root.val])
            if root.left:
                dfs(root.left, path+ [root.val], sum)
            if root.right:
                dfs(root.right, path + [root.val], sum)
        dfs(root, path, sum) # 想想把它传进去的第一个值的情况，就可以得出终止条件
        return ans