本组囊括二叉树各序遍历的题目,难度不等。
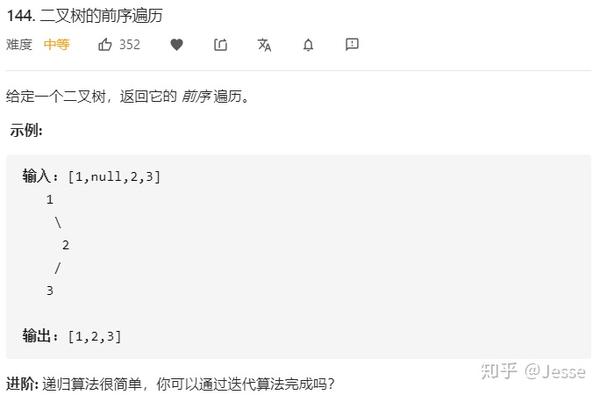
144. Binary Tree Preorder Traversal
题目描述:中等
解法一:递归
递归的dfs很简单,特别是用于前中后序三种遍历,只要该节点做好自己的事,就开启下一个顺序的节点的递归。
1 class Solution: 2 def preorderTraversal(self, root: TreeNode) -> List[int]: 3 if not root: 4 return [] 5 def dfs(root): 6 if root != None: 7 res.append(root.val) 8 dfs(root.left) 9 dfs(root.right) 10 res = [] 11 dfs(root) 12 return res
解法二:迭代
这里使用一种能够统一三种序遍历的迭代模板来写。(递归转迭代)
思路:递归的本质就是压栈,了解递归本质后就完全可以按照递归的思路来迭代。
怎么压,压什么?压的当然是待执行的内容,后面的语句先进栈,所以进栈顺序就决定了前中后序。
我们需要一个标志区分每个递归调用栈,这里使用None来表示。每个非空节点增加None节点,方便判断是否结束了一个递归调用栈,结束了才能返回该节点的值.。细节见注释
1 class Solution: 2 def preorderTraversal(self, root: TreeNode) -> List[int]: 3 if not root: 4 return [] 5 res = [] 6 stack = [root] 7 while stack: 8 node = stack.pop(-1) 9 if node == None: 10 node = stack.pop(-1) 11 res.append(node.val) 12 else: ## else后的顺序决定前中后序 13 if node.right: 14 stack.append(node.right) 15 if node.left: 16 stack.append(node.left) 17 stack.append(node) 18 stack.append(None) 19 return res
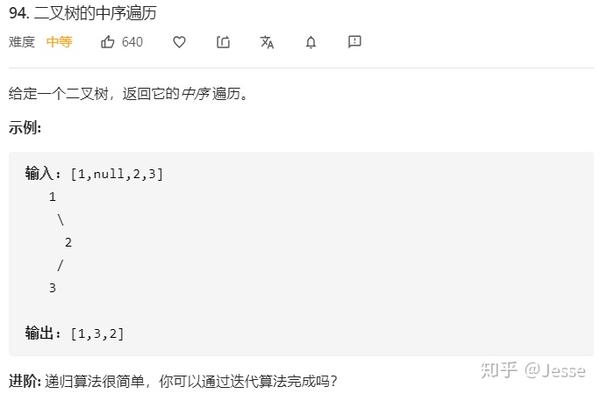
94. Binary Tree Inorder Traversal
题目描述:中等
解法一:递归
递归的dfs很简单,特别是用于前中后序三种遍历,只要该节点做好自己的事,就开启下一个顺序的节点的递归。
1 class Solution: 2 def preorderTraversal(self, root: TreeNode) -> List[int]: 3 self.res = [] 4 def dfs(root): 5 if root != None: 6 dfs(root.left) 7 self.res.append(root.val) 8 dfs(root.right) 9 dfs(root) 10 return self.res
解法二:迭代
这里使用一种能够统一三种序遍历的迭代模板来写。(递归转迭代)
思路:同上,注意else后的顺序决定了是前中还是后序。
1 class Solution: 2 def preorderTraversal(self, root: TreeNode) -> List[int]: 3 if not root: 4 return [] 5 stack = [root] 6 res = [] 7 while stack: 8 node = stack.pop(-1) 9 if node is None: 10 node = stack.pop(-1) 11 res.append(node.val) 12 else: 13 if node.right: 14 stack.append(node.right) 15 stack.append(node) 16 stack.append(None) 17 if node.left: 18 stack.append(node.left) 19 return res 20 # 时间复杂度:O(N) 21 # 空间复杂度:O(N)
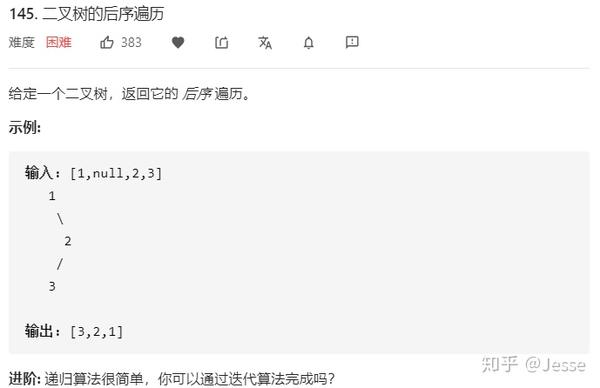
145. Binary Tree Postorder Traversal
题目描述:困难
解法一:递归
递归的dfs很简单,特别是用于前中后序三种遍历,只要该节点做好自己的事,就开启下一个顺序的节点的递归。
1 class Solution: 2 def preorderTraversal(self, root: TreeNode) -> List[int]: 3 if not root: 4 return [] 5 res = [] 6 def dfs(root): 7 if root != None: 8 dfs(root.left) # 框架递归左子树 9 dfs(root.right) # 框架递归右子树 10 res.append(root.val) # 本节点输出根节点值 11 dfs(root) 12 return res
解法二:迭代
这里使用一种能够统一三种序遍历的迭代模板来写。(递归转迭代)
思路:同上。
1 class Solution: 2 def preorderTraversal(self, root: TreeNode) -> List[int]: 3 if not root: 4 return [] 5 res = [] 6 stack = [root] # 对固定为初始化为root 7 while stack: 8 node = stack.pop(-1) # 每次循环都首先取出栈顶当做当前节点,并弹出 9 if node == None: # 空节点表示之前已经访问过了,现在需要处理除了递归之外的内容 10 node = stack.pop(-1) # 第二次弹出节点(彻底从栈中移除) 11 res.append(node.val) # 记录该节点值 12 13 ###### else之前的代码都是通用模板(前中后) ##### 只用改else后的代码 14 else:# 若遇到的是非空节点 15 stack.append(node) # 在右节点之前重新插入该节点,以便在最后处理(访问值) 16 stack.append(None) # None跟随node插入,标识已经访问过,还没有被处理 17 if node.right: # 先右后左,因为栈后进先出,先出左边的节点。 18 stack.append(node.right) 19 if node.left: 20 stack.append(node.left) 21 return res 22 # 时间复杂度:O(N) 23 # 空间复杂度:O(2N)最多
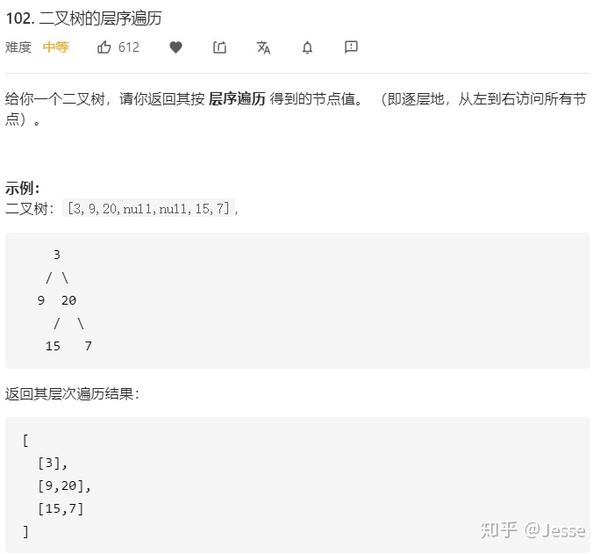
102. Binary Tree Level Order Traversal
题目描述:中等
解法一:BFS
二维数组,每次返回一层,广度优先遍历BFS,很明显地想到队列;
我们想到的层序是每次遍历完一个节点,再添加他的左右节点,这必须要求要先弹出上一层的节点,即先进来的节点所有我们借助队列来实现。
1 class Solution: 2 def levelOrder(self, root: TreeNode) -> List[List[int]]: 3 ans = [] # 存储结果的二维数组 4 if not root: 5 return ans 6 queue = [root] 7 while dueue: 8 size = len(queue) # 当前队列长度,即当前层有几个节点,全部加入一维数组中 9 res = [] # 每遍历完一层,则清空res 10 for i in range(size): 11 curr = dueue.pop(0) # 先进先出 12 if curr.left: 13 dueue.append(curr.left) 14 if curr.right: 15 dueue.append(curr.right) 16 res.append(curr.val) # 该层的所有节点加入队列 17 ans.append(res) # 该层的一维数组加入二维数组 18 return ans 19 # 时间复杂度:每个点进队出队各一次,故渐进时间复杂度为O(n)。 20 # 空间复杂度:队列中元素的个数不超过 n 个,故渐进空间复杂度为O(n)。
107. Binary Tree Level Order Traversal II
题目描述:简单
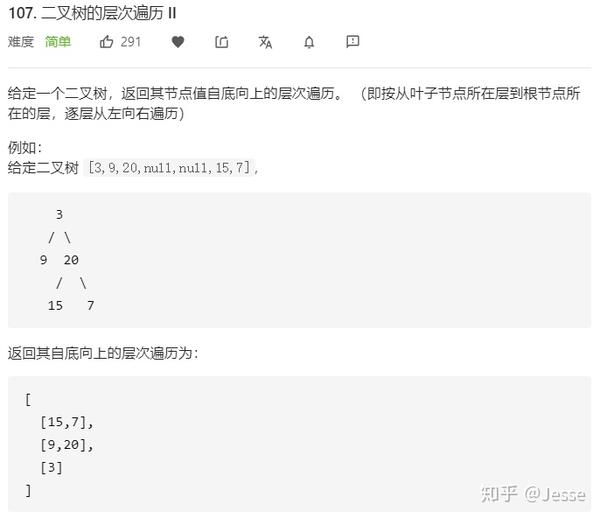
解法一:BFS
同上一题很像,也是要求输出二维数组:但这里需要的是反转输出。
取巧的方法,结果数组直接reverse即可。
1 class Solution: 2 def levelOrderBottom(self, root: TreeNode) -> List[List[int]]: 3 ans = [] # 存储结果的二维数组 4 if not root: 5 return ans 6 dueue = [root] # 初始队列 7 while dueue: 8 size = len(dueue) # 当前层的节点数 9 res = [] # 存储每层节点的一维数组,每遍历完一层清空 10 for _ in range(size): # 遍历当前层节点,都记录下来 11 curr = dueue.pop(0) # 先进先出 12 res.append(curr.val) # 当前层节点值依次加入数组 13 if curr.left: # 当前节点的左孩子加入队列 14 dueue.append(curr.left) 15 if curr.right: # 当前节点的右孩子加入队列 16 dueue.append(curr.right) 17 ans.append(res) # 加入一维数组 18 return ans[::-1] # 反转输出
103. Binary Tree Zigzag Level Order Traversal
题目描述:中等
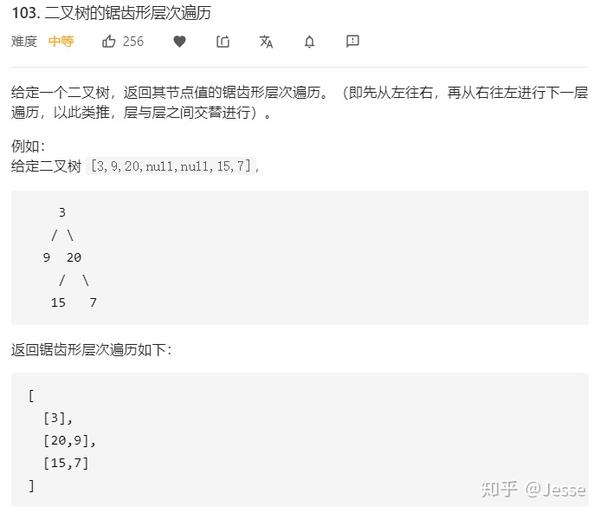
解法一:BFS
类似层序,使用迭代+BFS方法,借助队列实现;
关键在于如何层与层交替改变顺序,最取巧的方法,奇偶反转数组即可。
1 class Solution: 2 def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]: 3 if not root: 4 return [] 5 ans = [] # 存储结果的二维数组 6 dueue = [root] 7 i = 0 8 while dueue: 9 size = len(dueue) 10 res = [] 11 for _ in range(size): 12 curr = dueue.pop(0) 13 res.append(curr.val) 14 if curr.left: 15 dueue.append(curr.left) 16 if curr.right: 17 dueue.append(curr.right) 18 if i % 2 == 1:# 判断奇偶层,需要反转的时候反转 19 res = res[::-1] 20 ans.append(res) # 每次加一层 21 i += 1 # 每次自+1 22 return ans 23 # 时间复杂度:每个点进队出队各一次,故渐进时间复杂度为O(n)。 24 # 空间复杂度:队列中元素的个数不超过 n 个,故渐进空间复杂度为O(n)。