1、树
非线性结构,每个元素可以有多个前驱和后继。
树是 n (n>=0) 个元素的集合,不是set
-
- n = 0 时,称为空树
- 树只有一个特殊的没有前驱的元素,称为树的root
- 树种除了根节点外,其余元素只能有一个前驱,可以有0个或多个后继
递归定义:
-
- 树T 是n(n>=0)个元素的集合,n=0 时,称为空树。
- 有且只有一个特殊元素根,剩余元素都可以被划分为m个 互不相交的集合 T1,T2,T3..Tn,而每一个集合都是树,称为T 的子树subtree
- 子树也有自己的根
树的概念:
-
- 节点:树种的数据元素
- 节点的度 degree: 结点拥有的子树的数目称为度,记做d(v)。如图1,A结点两个子树,所以A结点的度为2,同理 结点D 的度3
- 叶子结点:结点的度为 0,称为叶子的结点leaf,终端结点,末端结点。
- 分支结点:结点的度不为0,称为非终端结点 或 分支结点
- 分支:结点之间的关系
- 内部节点:除根节点外的分支结点,当然也不包括叶子结点
- 树的度是树内各节点的度的最大值,D 的结点度最大为3,所以树的度为3
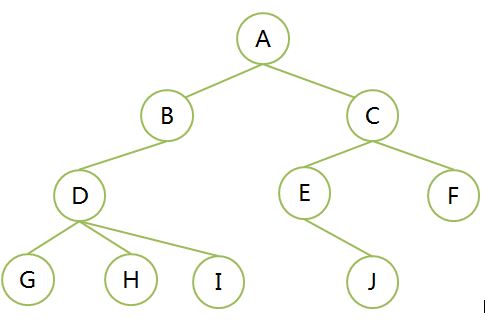
图1
-
- 孩子结点 :结点的子树的根节点成为该节点的孩子
- 双亲节点:一个节点是它各子树的根结点的双亲
- 兄弟结点:具有相同双亲结点 的结点
- 祖先结点:从根结点到该节点所经过分支上所有的结A,B,D都是G叶子的祖先结点
- 子孙结点:结点的所有子树上的结点都称为该结点的子孙,B的子孙结点D,GHI
- 结点层次(level):根结点为第一层,根的孩子为第二层,以此来类推 记做L(v)
- 。。。。。。。概念性东西,已经上传文件,有需要私聊!