背包问题

一、问题描述

---

 给定n种物品和一个背包，物品i(1≤i≤n)的重量是w_i，其价值为v_i，背包的容量为C。对每种物品只有两种选择：装入背包或者不装入背包。如何选择装入背包的物品，使得装入背包中物品的总价值最大？

二、分析与求解

---

这是一个经典的动态规划问题。容易证明，其满足最优子结构性质：即设(x₁, x₂, ..., x_n)是该问题的一个最优解（其中x_i=1表示放入物品i，x_i=0表示不放入），则(x₁, x₂, ..., x_k-1, x_k+1, ..., x_n)一定是原问题去除物品k后得到的子问题的最优解。

2.1 0/1背包问题

首先我们看一下背包问题的一个特例：0/1背包问题。（例题见于：Openjudge-0/1背包问题）

在此问题中，每种物品只有一件。于是，对于第i件物品，只有两种选择：放入背包或者不放入。最优解的递推表达式：

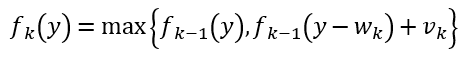
其中f_k(y)表示背包容量为y且只能取前k种物品的条件下，可以放入的物品的最大总价值。

为了在求得最大总价值后，找到对应的最优解，还需要标记函数。令标记函数I_k(y)表示背包容量为y且只能取前k种物品的条件下，放入的物品的最大序号，则有

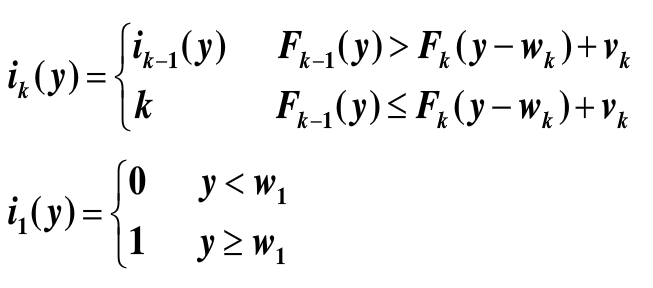
于是，我们可以写出0/1背包问题的代码：

『C++』

#include <iostream>
#include <algorithm>
using namespace std;
#define maxn 200
#define maxw 200

int n, C;

void TraceBack(int (*I)[maxn], int *w, int W) {
    int x[maxn] = {};
    int y = W, k = n;

    while (I[k][y] != 0) {
        while (I[k][y] == k) {
            y -= w[k];
            x[k]++;
        }
        k = I[k][y];
    }
    for (int i = 1; i <= n; i++) 
        printf("%d
", x[i]);
    
    return;
}

int main()
{
    while (cin >> n >> C) {
        int w[maxn] = {}, v[maxn] = {};
        int F[maxn][maxw] = {};
        int I[maxn][maxw] = {};
        int W[maxn][maxn] = {};
        for (int k = 1; k <= n; k++) {
            cin >> w[k] >> v[k];
        }
        for (int k = 1; k <= n; k++) {
            for (int y = 0; y <= C; y++) {
                if (y >= w[k] && F[k - 1][y] < F[k - 1][y - w[k]] + v[k]) {
                    F[k][y] = F[k - 1][y - w[k]] + v[k];
                    W[k][y] = W[k - 1][y - w[k]] + w[k];
                    I[k][y] = k;
                }
                else {
                    F[k][y] = F[k - 1][y];
                    W[k][y] = W[k - 1][y];
                    I[k][y] = I[k - 1][y];
                }
            }
        }

        printf("%d
", F[n][C]);

        TraceBack(I, w, W[n][C]);
    }

    //system("pause");
    return 0;
}

2.2 背包问题

若同一种物品可以放入多个，则标记函数同上，而只需将递推方程改为如下即可：