前言:Caustics光线刻蚀效果极大的影响着存在透明光学物体场景的真实性。光线在透明物体里发生衰减与二次折射,最终汇聚在一个小区域内,导致这个区域的能量比周围的光子密度高的多。比如一把放大镜将太阳光聚焦成一个光斑就体现了这种现象,在水底也会发生大面积的刻蚀亮斑。人们已经可以使用光线跟踪技术模拟这种效果,尤其是Maxwell Render甚至可以模拟三棱镜折射的效果。随着GPU计算能力的发展,在实时程序中也实现这种特效已经成为可能。本文基于《Caustics Mapping: An Image-space Technique for Real-time Caustics》
Caustics Mapping光线刻蚀效果在真实世界中很常见,但是在基于光栅化的实时渲染程序中几乎还没有使用,而在离线渲染的应用中比如电影的制作则无需顾忌硬件性能等等限制,画面质量才是最重要的。这是因为,Caustics几乎完全是一种几何光学现象,光线在透明介质入射与出射,发生两次折射,光线会汇聚在一块很小的区域上,形成一个耀眼的亮斑或是其它的形状的亮斑。基于光栅化工作的硬件既无法在整个场景中模拟光线的过程,也无法提供随机内存访问功能。而且我觉得,由于2D应用几乎是不会淘汰的,所以说PC平台上的图形加速硬件还依旧会是以光栅化工作。未来,最为极端的情况莫过于诞生另外一个类似Voodoo的时代,GPU在保留了具有高度可编程能力的光栅化核心后,再整合一个光线跟踪核心的硬件。其实这也不是不可能,Saarland Universtät的OpenRT项目就已经实现了光线跟踪硬件。
James Arvo在SIGGRAPH 86上发布了一篇具有相当分量的文章,《Backward Ray Tracing》,即后向光线跟踪,提出了如何从光源开始进行光线跟踪计算刻蚀的技术。后来由Henrik Wann Jensen于1993-1994年在他攻读博士期间发明了Photon Mapping算法,并1995年-1996年公开了相应的Paper。Photon Mapping最大的优点就是可以快速计算场景的全局光照Gobal Illumination,当然也包括刻蚀效果的生成。2003年《Graphic Hardware》杂志上,这几位来自Stanford的图形学界重量级人物,包括Henrik Wann Jensen、Pat Hanrahan、Timothy J. Purcell等人发表了一遍论文《Photon Mapping on Programmable Graphic Hardware》,提出了如何用GPU通过Photon Mapping实现全局光照。
这里展示了一种基于图象空间的刻蚀渲染技术,优点是实现简单而且速度快,和光线跟踪软件离线生成的效果图并没有多么显著的差距,是值得在实时渲染程序中加入的特效。整个算法类似于Photon Mapping,也分为两步,第一步是生成刻蚀纹理,第二步是将此纹理用于散射表面的渲染,也就是在接受刻蚀光线的物体上进行正确的贴图,简称为Receivers。
下面开始详细分析具体的步骤。直观看来很像Shadow Mapping,不妨留意对比一下看看。
A.获得刻蚀接受体的每个Primitive的世界坐标。生成PosTex。
B.获得光学折射物体的世界坐标与表面法向量。使用MRT。
C.生成刻蚀纹理。使用上一步获得的Vertex Grid Texture,沿着光线的折射方向向Reciever发射光线。这一步是最重要的,在后面将详细的解释如何去做。
D.从摄像机位置,使用刻蚀纹理渲染场景。
下面开始详细的解释如何实现过程C。刻蚀纹理是通过从光源渲染“可折射”的顶点获得的。所谓的“可折射”的顶点其实就是造成刻蚀现象的光学模型的靠近接受物体的顶点,类似于用这些顶点模拟了一个光子跟踪的过程。伪代码如下:
 for each vertex v do
for each vertex v do r = Refract( LightDirectionVector )
r = Refract( LightDirectionVector ) P = EstimateIntersection( v.position,r,ReceiverGeometry )
P = EstimateIntersection( v.position,r,ReceiverGeometry ) v.position = P
v.position = P return v
return v
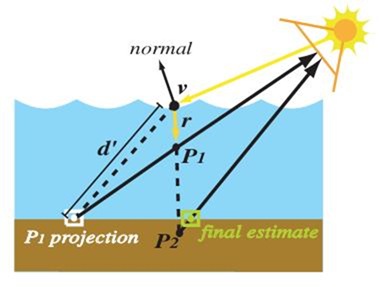
值得注意的是,这些经过Vertex Shader处理过后的顶点很有可能聚集在了一个块很小的区域内,这也就相当于模拟了光线的聚集。在接下来的Pixel Shader中,每个顶点的亮度使用Alpha通道混合进行累计。我们本质上需要的是折射光线与接受物体的交点。光线跟踪软件当然需要进行大量的三角形求交计算,目前当然根本无法使用在实时渲染的应用中。后面将展示如何找到正确的交点,使用Newton-Raphson(NR)迭代法。首先让我们看一下示意图:
v是光线发生折射的点,r是折射后的方向(假设已化为单位向量),则P = v + d*r,所以说,正确的估计交点也就是找到一个正确的d。在刚开始时,我们将d设为1,假设P1是交点,于是上式写成P1 = v + 1*r。然后我们将P1投射到以光源为视点的场景中去,随后使用P1采样PosTex,获得坐标v',求出与v的新距离d',带入上式获得P2。然后再用P2重复这个过程。伪代码如下:
 float3 EstimateIntersection ( float3 v, float3 r, sampler posTexture ) {
float3 EstimateIntersection ( float3 v, float3 r, sampler posTexture ) { float3 P1 = v + 1.0*r ;
float3 P1 = v + 1.0*r ; float4 texPt = mul( float4( P1, 1 ) , mViewProj );
float4 texPt = mul( float4( P1, 1 ) , mViewProj ); float2 tc = float2(0.5*(texPt.xy/texPt.w)+float2(0.5,0.5));
float2 tc = float2(0.5*(texPt.xy/texPt.w)+float2(0.5,0.5)); tc.y = 1.0f - tc.y;
tc.y = 1.0f - tc.y; float4 recPos = tex2D(posTexture, tc);
float4 recPos = tex2D(posTexture, tc); float4 P2 = v +distance(v,recPos.xyz)*r;
float4 P2 = v +distance(v,recPos.xyz)*r; texPt = mul( float4( P2, 1 ) , mViewProj );
texPt = mul( float4( P2, 1 ) , mViewProj ); tc = float2(0.5*(texPt.xy/texPt.w)+float2(0.5,0.5));
tc = float2(0.5*(texPt.xy/texPt.w)+float2(0.5,0.5)); tc.y = 1.0f - tc.y;
tc.y = 1.0f - tc.y; return recPos = tex2D(posTexture, tc);
return recPos = tex2D(posTexture, tc); }
}
注意,上面的伪代码只进行了2次迭代,重要的是它所展示的过程。下面我们讨论如何使用NR求根法获得准确的结果,而且NR是在Pixel Shader中进行直接的计算,比其它的方法都要快得多。通过上面的过程,我们可以很简单的构造这样的关系:
y[i] = PosTexture(x[i])
f(x[i]) = distance(x[i],y[i])
PosTexture函数的作用很直观,通过将x[i]投射到PosTex上,获得一个顶点坐标。由此我们可以知道,假设我们准确的找到了一个最精确的点,那么f(x[i]) = 0,因为我们从PosTex中找到了它本身。由此,一切问题都归为与f()密切相关。对于Pixel Shader,每一次迭代都需要2次纹理采样操作,为了减少操作次数,我们只有让结果尽量逼近。每次以迭代操作都好像P1与P2在反复的循环计算,仿佛在v处画了一个半径为d'的圆,反反复复的测试。事实上,每一次迭代都能够很快的逼近。对于一个非常不规则的物体来说,进行5次迭代后误差几乎可以忽略,而对于很规则的物体来说2次足够。伪代码如下:
 float rayGeoNP(float3 pos, float3 dir, float4x4 mVP, sampler posTex, int num_iter)
float rayGeoNP(float3 pos, float3 dir, float4x4 mVP, sampler posTex, int num_iter) {
{ float eps = 0.1;
float eps = 0.1; float2 tc = float2(0.0,0.0);
float2 tc = float2(0.0,0.0); // initial guess
// initial guess float x_k = 0.10;
float x_k = 0.10; for(int i=0;i<num_iter;i++)
for(int i=0;i<num_iter;i++) {
{ // f(x_k)
// f(x_k) float3 pos_p = pos + dir*x_k;
float3 pos_p = pos + dir*x_k; tc = getTC(mVP, pos_p);
tc = getTC(mVP, pos_p); float3 newPos1 = tex2D(posTex, tc);
float3 newPos1 = tex2D(posTex, tc); float f_x_k = distance(newPos1 , pos_p);
float f_x_k = distance(newPos1 , pos_p); float3 pos_q = pos + dir*(x_k+eps);
float3 pos_q = pos + dir*(x_k+eps); tc = getTC(mVP, pos_q);
tc = getTC(mVP, pos_q); float3 newPos2 = tex2D(posTex, tc);
float3 newPos2 = tex2D(posTex, tc); float f_x_k_eps = distance(newPos2 , pos_q);
float f_x_k_eps = distance(newPos2 , pos_q); float deriv = (f_x_k_eps - f_x_k)/eps;
float deriv = (f_x_k_eps - f_x_k)/eps; // the newton raphson iteration
// the newton raphson iteration x_k = x_k - (f_x_k/deriv);
x_k = x_k - (f_x_k/deriv); }
} return x_k;
return x_k; }
}
这个函数返回的就是d,由此我们可以找到足够准确的光线与接受物体的交点坐标。现在我们有了顶点,下面就是计算累计亮度。由于透明物体的不规则特性,在接受物体上投射的亮斑不仅仅受光能影响也受阴影影响。所以,我们利用加权处理每个顶点累计的亮度值,公式如下:
φ[i] = dot(N[i],L[i])/V
V是透明物体背对着光源的那个面的面积,N[i]是表面的法向量,L[i]是射入的光线向量。V可以简单的使用遮挡查询获得通过深度测试的象素个数再除以RenderTarget渲染目标的总象素数目得到。
学习过光线在大气中的散射性质以及在各向同性介质中的衰减的朋友知道,光线的能量是以指数衰减的,我们有下面的式子:
I = I0*exp(-Ka*d)
I0是入射光的光强,Ka是物体的吸收系数,d是光线在介质中的传输距离。如何获得距离大家可以看我的上一篇文章《GPU空间的精确折射模拟》一文,Wyman使用多通道技术实现了双次折射。如果渲染的是水刻蚀则不需要额外的计算,只需要获得水面顶点与接受物体的距离就可以了。
综合评价这种技术,我们很容易的发现,它的局限和碰到的问题和Shadow Mapping一样,都存在走样与失真问题,解决的方法无非是对摄像机的位置进行处理以及使用Polygon Offset。我们可以仿造《GPU GEMS 1》中的《Omidirectional Shadow Mapping全方位的阴影映射》一文所展示的立方体贴图阴影技术减少失真,不过这样带来的象素填充率要求又高了不少。
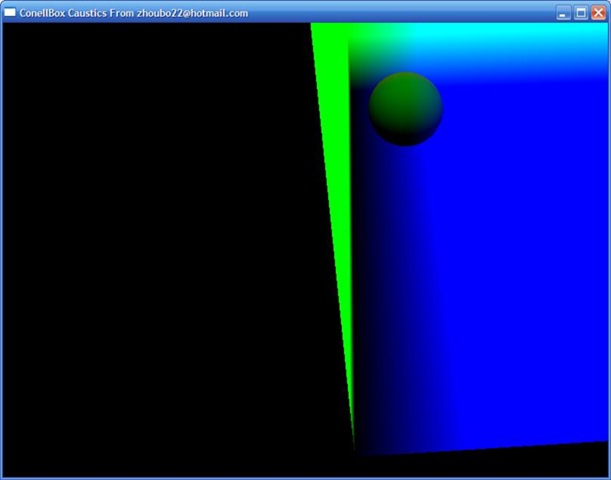
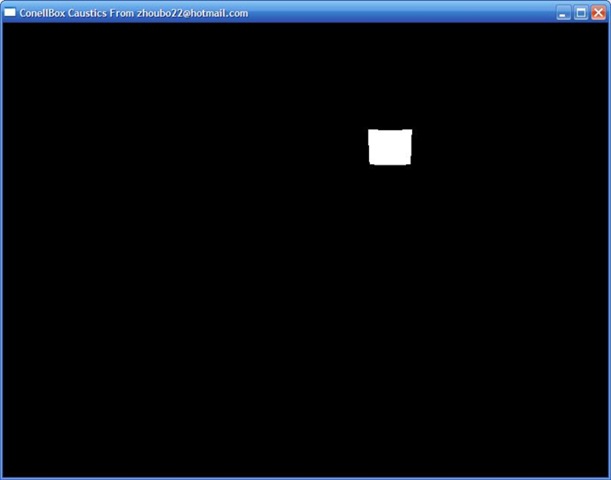
其实这张图的颜色是错误的,因为OpenGL无法显示RGBA32F_ARB格式,那些浮点数都经过了Clamp,所以你看到的是一片绿一片蓝,真正的RGBA32F_ARB渲染目标是不可见的,但是在逻辑上是正确的。下面是刻蚀图,仅仅是一片白斑。经过多次试验,8次迭代可以或者最好的结果。如果顶点网格比较少,甚至可以看到一个一个个的白点,好像Photon Map一样。
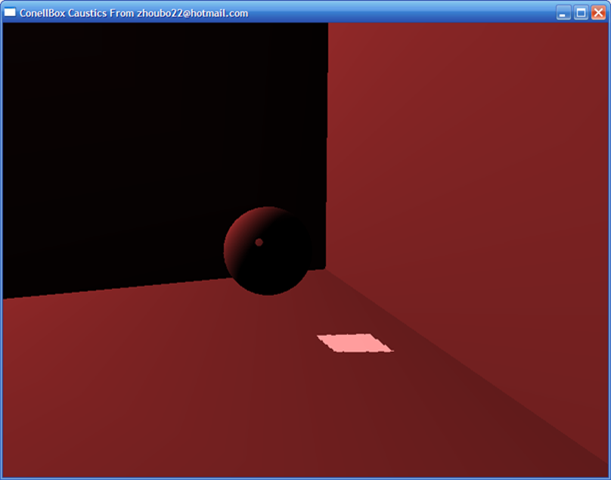
随后我们要做的就是,把CAUSTICS MAP投射到场景的Receiver上去,然后再把Refractor渲染出来,加上立方体映射、折射等等。最终的图如下,没有纹理,没有立方体贴图,没有多重采样抗锯齿,甚至光照都是最不精确的,只有纯粹的白色刻蚀。我不知道如何在使用Shader的情况下做Alpha混合,知道的请教我一下,不甚感激!
提供简易DEMO下载。整个程序使用了4个Shader,1个FBO,4个RGBA32F_ARB纹理,运行起来占用内存70M左右。由于需要在Vertex Shader中进行纹理采样,所以需要支持Shader Model 3的GPU,NVIDIA Geforce6系列以上或者ATi Radeon X1300以上。我使用的是Acer 5572ANWXCi 7300go。 其中最重要的PASS3的Shader代码如下,8次迭代,效果完美。
2
3 vec3 getTC(mat4 m,vec3 v)
4 {
5 vec4 p = m*vec4(v,1.0);
6 p.xy = 0.5*(p.xy + p.ww);
7 p.z = 0.5*(p.z + p.w + 0.122);
8 return p.xyz;
9 }
10
11 float rayGeoNP(vec3 pos, vec3 dir, mat4 mVP,sampler2D posTex, int num_iter)
12 {
13 float eps = 0.1;
14 vec2 tc = vec2(0.0,0.0);
15 // initial guess
16 float x_k = 0.10;
17 for(int i=0;i<num_iter;i++)
18 {
19 // f(x_k)
20 vec3 pos_p = pos + dir*x_k;
21 tc = getTC(mVP, pos_p).st;
22 vec3 newPos1 = texture2D(posTex, tc).xyz;
23 float f_x_k = distance(newPos1 , pos_p);
24 // f(x_k + eps)
25 vec3 pos_q = pos + dir*(x_k+eps);
26 tc = getTC(mVP, pos_q).st;
27 vec3 newPos2 = texture2D(posTex, tc).xyz;
28 float f_x_k_eps = distance(newPos2 , pos_q);
29 float deriv = (f_x_k_eps - f_x_k)/eps;
30 // the newton raphson iteration
31 x_k = x_k - (f_x_k/deriv);
32 }
33 return x_k;
34 }
35
36 void main()
37 {
38 vec3 N = normalize(gl_NormalMatrix*gl_Normal);
39 vec3 P = normalize(vec3(gl_ModelViewMatrix*gl_Vertex));
40 vec3 R = refract(P,N,0.76);
41 P = P + rayGeoNP(P,R,gl_ModelViewProjectionMatrix,PosTexture,8)*R;
42 gl_Position = gl_ModelViewProjectionMatrix*vec4(P,1.0);
43 }
44
后记:8月11号后很想找个地方实习,游戏行业、设计行业、或者是木材行业,长三角地区比如南京、上海都可以,自掏腰包也愿意,只希望找个地方实践一下,对我感兴趣的朋友请联系我。