图的最短路径-----------SPFA算法详解（TjuOj2831_Wormholes）

这次整理了一下SPFA算法，首先相比Dijkstra算法，SPFA可以处理带有负权变的图。（个人认为原因是SPFA在进行松弛操作时可以对某一条边重复进行松弛，如果存在负权边，在多次松弛某边时可以更新该边。而 Dijkstra 算法如果某一条边松弛后就认为该边已经是该连接点到源点的最短路径了，不会重复检查更新。 Dijkstra只能保证局部最优解而不会保证该解是全局最优解）

实现方法：

　　建立一个队列，初始时队列里只有起始点，再建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。然后执行松弛操作，用队列里有的点作为起始点去刷新到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。

判断有无负环：
　　如果某个点进入队列的次数超过N次则存在负环（SPFA无法处理带负环的图，但是可以判断是否出现负权环）

 

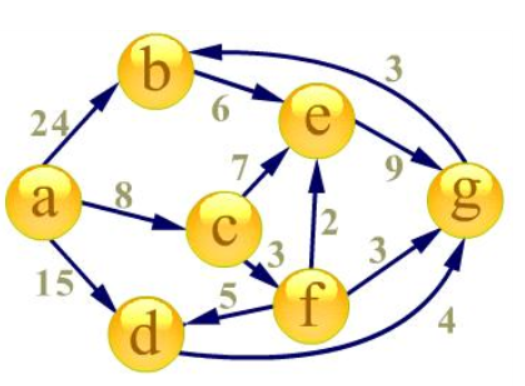
首先建立起始点a到其余各点的
最短路径表格

                                  

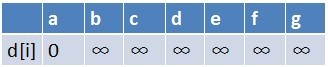
首先源点a入队，当队列非空时：
　１、队首元素（a）出队，对以a为起始点的所有边的终点依次进行松弛操作（此处有b,c,d三个点），此时路径表格状态为：

                                  

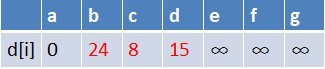
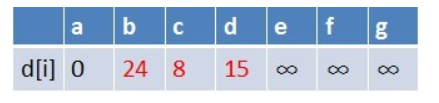
在松弛时三个点的最短路径估值变小了，而这些点队列中都没有出现，这些点
需要入队，此时，队列中新入队了三个结点b,c,d

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e点），此时路径表格状态为：

                                 

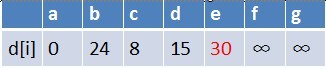
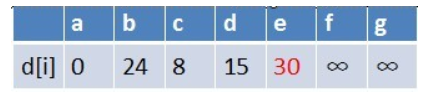
在最短路径表中，e的最短路径估值也变小了，e在队列中不存在，因此e也要
入队，此时队列中的元素为c，d，e

队首元素c点出队，对以c为起始点的所有边的终点依次进行松弛操作（此处有e,f两个点），此时路径表格状态为：

                                 

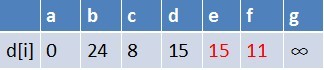
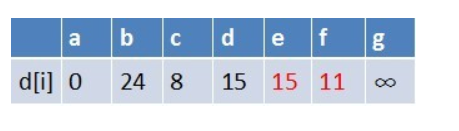
在最短路径表中，e，f的最短路径估值变小了，e在队列中存在，f不存在。因此
e不用入队了，f要入队，此时队列中的元素为d，e，f

 队首元素d点出队，对以d为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

    

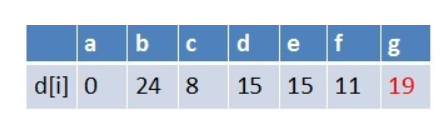
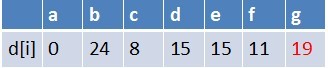
在最短路径表中，g的最短路径估值没有变小（松弛不成功），没有新结点入队，队列中元素为f，g

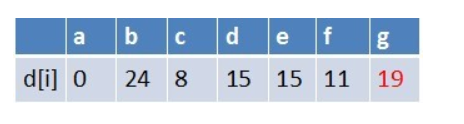
队首元素f点出队，对以f为起始点的所有边的终点依次进行松弛操作（此处有d，e，g三个点），此时路径表格状态为：

在最短路径表中，e，g的最短路径估值又变小，队列中无e点，e入队，队列中存在g这个点，g不用入队，此时队列中元素为g，e

队首元素g点出队，对以g为起始点的所有边的终点依次进行松弛操作（此处只有b点），此时路径表格状态为：

   

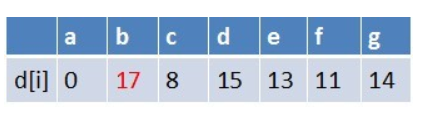
在最短路径表中，b的最短路径估值又变小，队列中无b点，b入队，此时队列中元素为e，b
队首元素e点出队，对以e为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

 

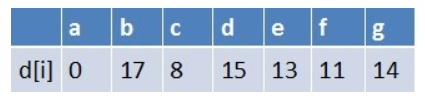
在最短路径表中，g的最短路径估值没变化（松弛不成功），此时队列中元素为b

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e这个点），此时路径表格状态为：

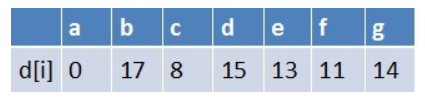
在最短路径表中，e的最短路径估值没变化（松弛不成功），此时队列为空了

最终a到g的最短路径为１４

至此，算法结束。

最后，需要注意如果存在负权环的话，那么，队列中永远不可能为空，因为在某次更新时候d[a]会被更新为负值，进而d数组中的每条边都会被循环更新。因为正常每个点入队的次数不会超过总的点数，所以某点入队次数超出总点数则必定出现负权环。利用该性质可以判断是否出现负权环。

该方法在TjuOj2831中的实现如下：

题意是FJ有很多农场，每个农场有很多双向通路，也有单向的虫洞，从通路到达不同农场会花费时间，从虫洞到达不同农场会回到过去的某一个时刻（即权为负），如果有一种方式（环）使得FJ通过某些农场回到原点的同时，时间也回到过去的时刻（发现负权环），那么输出YES，否则NO。

While exploring his many farms, Farmer John has discovered a number of amazing wormholes. A wormhole is very peculiar because it is a one-way path that delivers you to its destination at a time that is BEFORE you entered the wormhole! Each of FJ's farms comprises N (1 ≤ N ≤ 500) fields conveniently numbered 1..N, M (1 ≤ M ≤ 2500) paths, and W (1 ≤ W ≤ 200) wormholes.

As FJ is an avid time-traveling fan, he wants to do the following: start at some field, travel through some paths and wormholes, and return to the starting field a time before his initial departure. Perhaps he will be able to meet himself :) .

To help FJ find out whether this is possible or not, he will supply you with complete maps to F (1 ≤ F ≤ 5) of his farms. No paths will take longer than 10,000 seconds to travel and no wormhole can bring FJ back in time by more than 10,000 seconds.

Input

* Line 1: A single integer, F. F farm descriptions follow.

* Line 1 of each farm: Three space-separated integers respectively: N, M, and W

* Lines 2..M + 1 of each farm: Three space-separated numbers (S, E, T) that describe, respectively: a bidirectional path between S and E that requires T seconds to traverse. Two fields might be connected by more than one path.

* Lines M + 2..M + W + 1 of each farm: Three space-separated numbers (S, E, T) that describe, respectively: A one way path from S to E that also moves the traveler back T seconds.

Output

* Lines 1..F: For each farm, output "YES" if FJ can achieve his goal, otherwise output "NO" (do not include the quotes).

Sample Input

2
3 3 1
1 2 2
1 3 4
2 3 1
3 1 3
3 2 1
1 2 3
2 3 4
3 1 8

Sample Output

NO
YES

Input Details

Two farm maps. The first has three paths and one wormhole, and the second has two paths and one wormhole.

Output Details

For farm 1, FJ cannot travel back in time.
For farm 2, FJ could travel back in time by the cycle 1->2->3->1, arriving back at his starting location 1 second before he leaves. He could start from anywhere on the cycle to accomplish this.

/*
 * 2831_Wormholes.cpp
 *
 *  Created on: 2018年11月15日
 *      Author: Jeason
 */
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <cstring>
#include <vector>
#include <queue>
#define N 1000
using namespace std;
int numPoint,numPath,numHole;
int T,temp,temA,temB,temLength;
int dist[N],num_visited[N];  //dist用于记录搜寻源点到各点的距离，num_visited用于记录每个点入队的次数；
int root;     //SPFA的搜寻起点；
queue<int> Q;
struct node
{
    int nextPoint;
    int length;
};
vector <node> Tree[N];

void readData(){
    cin >> numPoint >> numPath >> numHole;
    for(int i = 0 ; i < numPath ;i++){
        cin >> temA >> temB >> temLength;
        node P1,P2;
        P1.nextPoint = temB;
        P1.length = temLength;
        P2.nextPoint = temA;
        P2.length = temLength;
        Tree[temA].push_back(P1);
        Tree[temB].push_back(P2);
        root = temA;      //找起点；
    }
    for(int i = 0 ; i < numHole ;i++){
        node P;
        cin >> temA >> temB >> temLength;
        P.nextPoint = temB;
        P.length = 0 - temLength;
        Tree[temA].push_back(P);
    }
}

void init()
{
    for( int i = 0; i < N; i++ )
        Tree[i].clear();
    memset(num_visited,0,sizeof(num_visited));
}

int SPFA()
{
    while(!Q.empty()){

        temp = Q.front();
        Q.pop();
//        cout << temp << "点出队" << endl;
        if(num_visited[temp] > numPoint)
            return 0;  //返回0说明有负权环出现，Q队列一直不为空，死循环
        for(int i = 0; i < Tree[temp].size(); i++){ //对出队的每个点进行遍历,并进行松弛
            if(dist[ Tree[temp][i].nextPoint ] > dist[temp] + Tree[temp][i].length ){
                dist[ Tree[temp][i].nextPoint ] = dist[temp] + Tree[temp][i].length;
                Q.push(Tree[temp][i].nextPoint);
//                cout <<  Tree[temp][i].nextPoint << " > " << temp << " + " << Tree[temp][i].length << endl;
//                cout << "已被松弛：" << temp <<"--->" << Tree[temp][i].nextPoint <<endl;
//                cout << Tree[temp][i].nextPoint << "点入队" << endl;
                num_visited[Tree[temp][i].nextPoint]++;
            }
        }
    }
    return 1;   //返回1说明SPFA操作成功，没有负权环出现
}

int main()
{
    cin >> T;
    while(T--){
        init();
        readData();

        for(int i = 0; i < N;i++)
            dist[i] = 999999;
        Q.push(root);
//        cout << root << "点入队" << endl;
        dist[root] = 0;
        num_visited[root]++;
        if ( SPFA() )
            cout << "NO" << endl;
        else
            cout << "YES" <<endl;
    }
    return 0;
}


/*

Sample Input
2
3 3 1
1 2 2
1 3 4
2 3 1
3 1 3

3 2 1
1 2 3
2 3 4
3 1 8
Sample Output
NO
YES

 * */