最近对问题
1. 问题
n个点在公共空间中,求出所有点对的距离最小值。
2. 解析
① 对所有的点按照x坐标从小到大排序。根据下标进行分割,使得点集分为两个集合。
② 递归的寻找两个集合中的最近点对。取两个集合最近点对中的最小值min(dis_left,dis_right)。
③ 最近距离不一定存在于两个集合中,可能一个点在集合A,一个点在集合B,而这两点间距离小于dis。这其中如何合并是关键。根据递归的方法可以计算出划分的两个子集中所有点对的最小距离dis= min(dis_left,dis_right)。那么一个点在集合A,一个在集合B中的情况,可以针对此情况,用之前分解的标准值,即按照x坐标从小到大排序后的中间点的x坐标作为mid,划分一个[mid−dis,mid+dis]区域,如果存在最小距离点对,必定存在这个区域中。
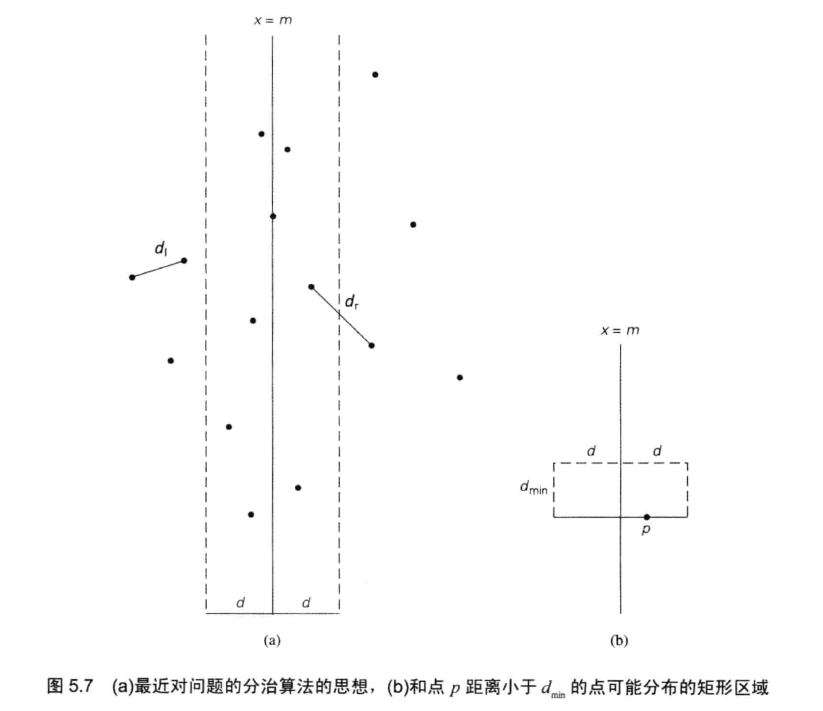
之后只需要根据[mid−dis,mid]左边区域的点来遍历右边区域[mid,mid+dis]的点,即可找到是否存在小于dis距离的点对。
3. 设计
1 #include<stdio.h> 2 #include<math.h> 3 #include<algorithm> 4 #include<vector> 5 using namespace std; 6 const int maxn = 1000 + 10; 7 struct Point { 8 int x, y; 9 Point(int _x = 0, int _y = 0) :x(_x), y(_y) {} 10 bool operator < (const Point& rhs)const { 11 return x < rhs.x; 12 } 13 }; 14 int n; 15 bool cmp(struct Point& a, struct Point& b) { //按照x坐标从小到大排序 16 return a.x < b.x; 17 } 18 bool cmp2(struct Point& a, struct Point& b) { //按照y坐标从小到大排序 19 return a.y < b.y; 20 } 21 double Dis(Point a, Point b) { 22 return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); 23 } 24 25 double ClosestPoint(vector<Point> points, int left, int right) { 26 if (right - left < 2)return 0x3f3f3f3f; 27 if (right - left == 2) { 28 return Dis(points[left], points[right - 1]); 29 } 30 if (right - left == 3) { 31 double d1 = Dis(points[left], points[right - 1]); 32 double d2 = Dis(points[left], points[right - 2]); 33 double d3 = Dis(points[right - 2], points[right - 1]); 34 return min(d1, min(d2, d3)); 35 } 36 int mid = (right + left) / 2; 37 int mm = points[mid].x; 38 double dl = ClosestPoint(points, left, mid); //左边区域最短距离 39 double dr = ClosestPoint(points, mid, right); //右边区域最短距离 40 double minn = min(dl, dr); 41 vector<Point>v; 42 for (int i = left; i < mid; ++i) { 43 if (mm - points[i].x <= minn) 44 v.push_back(points[i]); 45 } 46 for (int i = mid; i < right; ++i) { 47 if (points[i].x - minn <= mm) 48 v.push_back(points[i]); 49 } 50 sort(v.begin(), v.end(), cmp2); 51 double mindist = 0x3f3f3f3f; 52 for (int i = 0; i < v.size(); ++i) { //处理分隔线两边的点 53 for (int j = i+1; j < v.size(); ++j) { 54 if (abs(v[i].y - v[j].y) < minn) { 55 double d = Dis(v[i], v[j]); 56 if (d < minn) mindist = d; 57 } 58 else { 59 break; 60 } 61 } 62 } 63 return min(minn, mindist); 64 } 65 66 int main() { 67 vector<Point>points; 68 scanf("%d", &n); 69 for (int i = 1; i <= n; ++i) { 70 Point point; 71 scanf("%d %d", &point.x, &point.y); 72 points.push_back(point); 73 } 74 sort(points.begin(), points.end(), cmp); 75 printf("%.2f ", ClosestPoint(points, 0, n)); 76 }
4. 分析
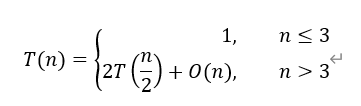
因此整体的时间复杂度为O(nlogn)。
5. 源码
https://github.com/JayShao-Xie/algorithm-work/blob/master/ClosestPoint.cpp