MMORPG programming in Silverlight Tutorial (8)A* Algorithm

    From this chapter, I will introduce map engine, it refer to 2 aspects, as follows:

    1) Implementation the map. Including map’s splitting, composing and rendering style.

    2) Implementation the objects of the map. Including obstruction, mask and transportation.

    Now let’s begin with path finding.

    At present, the most classic path finding algorithm is A*, there are many algorithms originate from it, for example, the Manhattan method. In this chapter, i don’t plan to introduce A* algorithm’s implementation. If you are interested, you can visit this article to study more:

http://www.codeguru.com/csharp/csharp/cs_misc/designtechniques/article.php/c12527/

    This guy implemented this algorithm in C#, so my friend Xuan Qin, referred to his implementation and wrote higher performance algorithm base on it. He named it QXGame_Silverlight3.dll. You can download it here: QXGame_Silverlight3.zip

    The picture below shows the high performance of this algorithm implementation. The brown grid stands for obstruction, the start point is the left top corner, the end point is the red grid in the center of the canvas. The blue grid stands for the shortest path. The algorithms cost 0.0030s to find the path, it is perfect.

    A* algorithm is difficult to understand, but it doesn’t matter whether you master it completely, we only care about how to use it in our game engine.

   1st, add reference to this dll, and declare its namespace in the code behind:

using QXGame_Silverlight3.AStar;

   2nd, init global variables:

//a matrix used for finding path
private byte[,] matrix = new byte[1024, 1024];

//the size of the unit grid
private int gridSize = 20;

//the start and end point of the moving animation
private Point start, end;

 

   The variable gridSize is very important. As we know, the game map is so large that we can’t define each grid is an obstruction or not, so we must scale down the coordinate, the gridSize is the ratio.

    For example, the window size is 800*600, supposed a point(80, 100) in the window, according to the ratio: gridSize =20, the point is converted to (80/20, 100/20) = (4, 5). It is convenient for us to implement every effect in different scenarios. I will explain this advantage in the following chapters.

    Attention, the matrix‘s Uppound must be the pow of 2; otherwise, A* algorithm will throw an exception. In our demo, it is 1024. It is enough. It is adjusted dynamically, I will talk about it in the following chapters.

    3rd, init matrix, as follows, we set its elements, default value is 1, and 0 stands for obstruction:

void InitMatrix()
{
    for (int y = 0; y < matrix.GetUpperBound(1); y++)
    {
        for (int x = 0; x < matrix.GetUpperBound(0); x++)
        {
            //default to 1, to stand for not obstraction
            matrix[x, y] = 1;
        }
    }

    //init obstruction
    for (int i = 0; i < 18; i++)
    {
        //set to 0, to stand for obstraction
        matrix[i, 12] = 0;

        rect = new Rectangle()
        {
            Fill = new SolidColorBrush(Colors.Red),
            Width = gridSize,
            Height = gridSize
        };

        Carrier.Children.Add(rect);

        Canvas.SetLeft(rect, i * gridSize);
        Canvas.SetTop(rect, 12 * gridSize);
    }

    //init obstruction
    for (int i = 12; i < 17; i++)
    {
        matrix[17, i] = 0;

        rect = new Rectangle()
        {
            Fill = new SolidColorBrush(Colors.Red),
            Width = gridSize,
            Height = gridSize
        };

        Carrier.Children.Add(rect);

        Canvas.SetLeft(rect, 17 * gridSize);
        Canvas.SetTop(rect, i * gridSize);
    }

    //init obstruction
    for (int i = 3; i < 18; i++)
    {
        matrix[i, 16] = 0;

        rect = new Rectangle()
        {
            Fill = new SolidColorBrush(Colors.Red),
            Width = gridSize,
            Height = gridSize
        };

        Carrier.Children.Add(rect);

        Canvas.SetLeft(rect, i * gridSize);
        Canvas.SetTop(rect, 16 * gridSize);
    }
}

    In the code snippet above, I init 3 obstruction regions, and add 18+5+15 = 38 rectangles in the canvas. They are all obstructions, filled in Red. The effect is as follows:

    The value of gridSize is not fixed. If the value is small, there will be so many small rectangle generated in the canvas; if the value is large, maybe it cannot describe the obstruction accurately. So you must adjust it in different scenarios.

    4th, Find path between start and end point.

    The start point is fixed, I init its value as (1, 1).

    In the method Carrier_MouseLeftButtonDown, we reset end point in the first 4 sentences.

private void Carrier_MouseLeftButtonDown(object sender, MouseButtonEventArgs e)
{
    //set end point's coordinate
    Point p = e.GetPosition(Carrier);
    int x = (int)p.X / gridSize;
    int y = (int)p.Y / gridSize;
    end = new Point(x, y);

    IPathFinder pathFinder = new PathFinderFast(matrix);
    pathFinder.Formula = HeuristicFormula.Manhattan;
    pathFinder.SearchLimit = 2000;   //the step number is less than 2000
    //pathFinder.Diagonals = false;

    var path = pathFinder.FindPath(start, end);
    if (path == null)
    {
        MessageBox.Show("Path is not existing");
        return;
    }

    for (int i = path.Count - 1; i >= 0; i--)
    {
        rect = new Rectangle()
        {
            Fill = new SolidColorBrush(Colors.Green),
            Width = gridSize,
            Height = gridSize
        };

        Carrier.Children.Add(rect);

        Canvas.SetLeft(rect, path[i].X * gridSize);
        Canvas.SetTop(rect, path[i].Y * gridSize);
    }
}

    Next, we use path finder algorithm, take matrix as the first parameter, A* algorithm will return an path array if there is a path between start and end point. I mark each element of the path array in green and locate all of them to their original point(path[i].X * gridSize, path[i].Y * gridSize).

    Now, press Ctrl+F5, and click on the canvas, we can see the effect as follows, A* algorithm find a green path for us, although it is not well optimized.

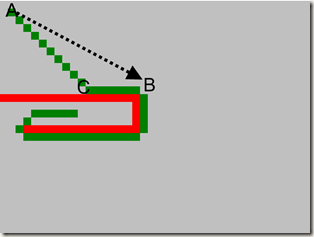
    There is still a problem left for us. As you can see in the picture as follow, why not go straight from A to B? It is shorter than the path: A->C->B. I will resolve it in the following chapters.

Summary: This chapter introduce A* algorithm and how to use it in our games.

    Next chapter, I will implement how to add keyFrame dynamically, so you can change the animation even the object is still moving. Please focus on it.

    Chinese friend, you can also visit this Chinese blog if you feel difficult to read English, http://www.cnblogs.com/alamiye010/archive/2009/06/17/1505346.html, part of my article is base on it.

    Demo download: http://silverlightrpg.codeplex.com/releases/view/40978