最小生成树(MST):[洛谷模版传送门]
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
——度娘百度百科
说白了就是给你一个图,把边权等都给你(特殊情况是相等的)。然后让这些节点全部都连成一颗树,问最小的代价是多少。
本篇blog会对kruskal算法进行详细讲解。其实是Prim掌握还不熟
kruskal算法是用的比较多的一类求最小生成树的算法。核心思想是贪心。程序要做的重要两步:
1.给边排序,比较的标准是边的权值,小的在前面。
2.开始从排序后开始枚举边,如果这条边的起点和终点已经联通,则不管,反之则加入。
为什么这个方法是对的呢?
请你思考一下:每个可以联通的点,因为已经排好了序,如果节点v还没有加入,现有一条(u,v)的边,肯定比其他到v的权值更小。
我们采取“逐个击破”的原则去做出这两步:
一.给边排序
这里有两种方案可以让边进行快速排序(当然你要手写快排我也不拦你)
1.为sort函数传入第三个参数
有兴趣的同学可以看一下sort

如果有同学问:为什么有两个sort函数?
C++是支持函数重载的,只要参数个数和类型不同,都可以同时存在
然后我们可以定义一个compare函数(其实很复杂的,目前可以先这么理解)
然后我们传参进去,穿的是compare函数的地址。
1 bool cmp(Edge x,Edge y){return x.dis<y.dis;}
2 sort(edge,edge+m,cmp);//注意这个地方cmp后面没有括号和参数!!!
这是第一种定义大小比较。
2.重载运算符'<'
在Edge的结构体内放上这样一行:
bool operator <(const Edge& A)const{ return dis<A.dis; }//const修饰符不要忘了!!!
这个时候可以直接sort。
二.枚举边,看终点是否已经连接
这个看上去很麻烦。。。判断联通是比较困难的,BFS和DFS都可以,但是——TLE会向你招手
那有没有一个比较简单易学的算法来实现呢?
我们发现:如果一个点和另一个点联通,他们之间是可以不管父亲儿子节点。
于是有同学想到了STL的容器set没错那个同学就是我
但是set太low了是错的。因为边排序后,生成(联通)每一条边并不一定相等。
所以我们需要一个高效简介的算法:并查集
我们只需要维护一个f数组,f[u]表示节点u的父亲。
再套一个函数find,用于找到u的最终祖先。
1 int find(int x){return f[x]==x?x:f[x]=find(f[x]);}//简洁
3 f[v]=u;//让v的的父亲变成u
所以,我们以洛谷测试为例:
krusal的过程是这样的:
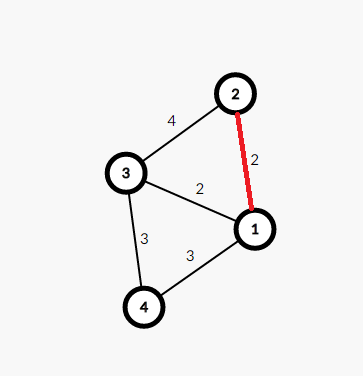
(1)ans+=2;
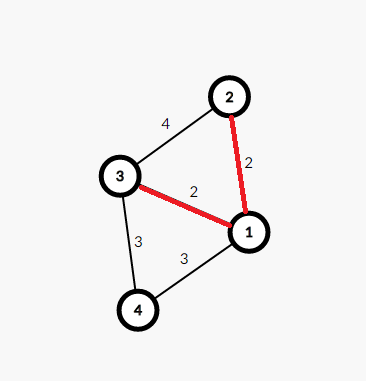
(2)ans+=2;
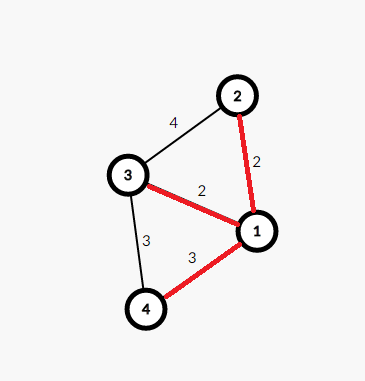
(3)ans+=3;
下面仍给出代码:
1 #include<bits/stdc++.h> 2 namespace Jason{ 3 inline int scan(int &x){ 4 int f=1;x=0;char s=getchar(); 5 while(s<'0' || s>'9'){if(s=='-') f=-1;s=getchar();} 6 while(s>='0' && s<='9'){x=x*10+s-'0';s=getchar();} 7 x*=f; 8 return 1;//返回1说明读入正常 9 } 10 inline int print(int x){ 11 if(x<0){putchar('-');x=-x;} 12 if(x>9)print(x/10);char s=x%10+'0'; 13 putchar(s); 14 return 1;//返回1说明输出正确 15 } 16 } 17 using namespace std; 18 using namespace Jason; 19 const int maxn=5005; 20 const int maxm=200005; 21 struct Edge{ 22 int s,t,dis; 23 bool operator <(const Edge A)const{ 24 return dis<A.dis; 25 } 26 }edge[maxm<<1]; 27 int n,m,tot=-1; 28 int f[maxn]; 29 //-----------------------------------------------数据结构和读入输出优化 30 void init(){for(int i=1;i<=n;++i)f[i]=i;} 31 inline int find(int x){return f[x]==x?x:f[x]=find(f[x]);} 32 //-----------------------------------------------并查集相关函数 33 bool cmp(Edge x,Edge y){return x.dis<y.dis;} 34 void add(int u,int v,int w) 35 { 36 edge[++tot].s=u; 37 edge[tot].t=v; 38 edge[tot].dis=w; 39 } 40 int kruskal(){ 41 int ans=0; 42 sort(edge,edge+m); 43 for(int i=0;i<m;++i) 44 { 45 int u=find(edge[i].s),v=find(edge[i].t); 46 if(u!=v) 47 ans+=edge[i].dis; 48 f[v]=u; 49 } 50 return ans; 51 } 52 int main() 53 { 54 scan(n),scan(m); 55 init(); 56 for(int i=0,x,y,z;i<m;++i)scan(x),scan(y),scan(z),add(x,y,z); 57 int ans=kruskal(); 58 print(ans); 59 putchar(' '); 60 return 0; 61 }
有一个动态算法可视网站[点我进入],里面有MST,Dijkstra,Bellman-Ford等算法,疯狂安利。