Mobius反演定理-BZOJ2154

This article is made by Jason-Cow.
Welcome to reprint.
But please post the article's address.

莫比乌斯定理（未完待续......）：

形式1：

$F(n)=\sum_{d|n}f(d) =>f(n)=\sum_{d|n}\mu (d)F(\frac{n}{d})$

形式2：

$F(n)=\sum_{n|d}f(d)=>f(n)=\sum_{n|d}\mu(\frac{d}{n})F(d)$

引理:

$\mu(x)=\left\{\begin{matrix} & & 1 (x=1) \\ & & 0(x\neq1 ) \end{matrix}\right.$

证明1：

右边= $f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})$ 带入左边等式，得

　　　 $=\sum_{d|n} \mu(d) \sum_{k|\frac{n}{d}} f(k)$

　　　　　　 $=\sum_{d|n}\sum_{k|\frac{n}{d}}\mu(d)f(k)$

　　　　　　 $=\sum_{k|n}\sum_{d|\frac{n}{k}}f(k)\mu(d)$

　　　　　　 $=\sum_{k|n}f(k)\sum_{d|\frac{n}{k}}\mu(d)$ 又 $\because$ $\mu(d)\neq 0$ 当且仅当 : $\frac{n}{k}=1$ ，即 $n=k$ 时，上式非 $0$

　　　　　 $=f(n)$

所以， $F(n)=\sum_{d|n}f(d) =>f(n)=\sum_{d|n}\mu (d)F(\frac{n}{d})$ 成立。

bzoj2154

$\sum_{i=1}^{n}\sum_{j=1}^{m}\frac{i*j}{\gcd(i,j)}$

$\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{g=1}^{n}\frac{i*j}{g}[\gcd(i,j)==g]$

$\sum_{g=1}^{n}\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}\frac{(i*g)(j*g)}{g}[\gcd(i,j)==1]$

$\sum_{g=1}^{n}\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*g*[\gcd(i,j)==1]$

$\sum_{g=1}^{n}g\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*[\gcd(i,j)==1]$

$\sum_{g=1}^{n}g\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*\sum_{d|\gcd(i,j)}\mu(d)$

$\sum_{g=1}^{n}g\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*\sum_{d|i,d|j}\mu(d)$

$\sum_{g=1}^{n}g\sum_{d=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{i=1}^{\left \lfloor \frac{n}{gd} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{gd} \right \rfloor}(i*d)*(j*d)*\mu(d)$

$\sum_{g=1}^{n}g\sum_{d=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\mu(d)d^{2}\sum_{i=1}^{\left \lfloor \frac{n}{gd} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{gd} \right \rfloor}i*j$

$\sum_{g=1}^{n}g\sum_{d=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\mu(d)d^{2}\sum_{i=1}^{\left \lfloor \frac{n}{gd} \right \rfloor}i\sum_{j=1}^{\left \lfloor \frac{m}{gd} \right \rfloor}j$

时间复杂度

$O(n \sum_{i=1}^{n}\frac{1}{i})=O(n(\ln(n)+C))/*C=0.57721566490153286060651209*/$

换元：令

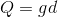
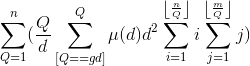
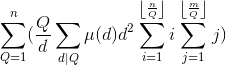
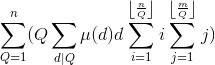
此题的精髓就一个字，模

 1 #include <algorithm>
 2 #include <iostream>
 3 #include <cstring>
 4 #include <cstdlib>
 5 #include <cstdio>
 6 #include <vector>
 7 #include <cmath>
 8 #include <queue>
 9 #include <map>
10 #include <set>
11 using namespace std;
12 #define file(x) freopen(x".in","r",stdin),freopen(x".out","w",stdout)
13 
14 const int mod=20101009,maxn=1e7+10;
15 int f[maxn],p[maxn],flag[maxn],cnt,S[maxn];
16 void init(int n,int m){
17   f[1]=1;
18   for(int i=2;i<=n;i++) {
19     if(!flag[i])p[++cnt]=i,f[i]=(1-i)%mod;
20     for(int j=1;j<=cnt && i*p[j]<=n;j++) {
21       flag[i*p[j]]=1;
22       if(i%p[j]==0){f[i*p[j]]=f[i]%mod;break;}
23       f[i*p[j]]=((long long)(f[i]%mod)*(f[p[j]]%mod))%mod;
24     }
25   }
26   for(int i=1;i<=m;i++)S[i]=((S[i]%mod)+((S[i-1]+i)%mod))%mod;
27 }
28 
29 int main(){
30   int n,m;scanf("%d%d",&n,&m);if(n>m)swap(n,m);
31   init(n,m);
32   int ans=0;
33   for(int Q=1;Q<=n;Q++)
34     ans=(ans+(((Q%mod)*(long long)f[Q]*(((long long)S[n/Q]*S[m/Q])%mod))%mod)%mod)%mod;
35   printf("%d
",(ans+mod)%mod);
36   return 0;
37 }

f (n) = \sum d | n μ (d) F (n d ) =

相关阅读:
Linq&Lumbda
PS颜色模式
 WPF绑定方式
 明三杰刘健
 齐有鲍叔，郑有子皮
 朱厚照
 管子&小白
 时间
 人外有人之神箭手养繇基篇
 楚共王
原文地址：https://www.cnblogs.com/JasonCow/p/6550441.html

Mobius反演定理-BZOJ2154

This article is made by Jason-Cow.Welcome to reprint.But please post the article's address.

莫比乌斯定理（未完待续......）：

形式1：

形式2：

This article is made by Jason-Cow.
Welcome to reprint.
But please post the article's address.