INT104-lab10 测试新数据集完成！[Multinomial Naive Bayes][MLE极大似然估计][二分类]

这里直接是一个二分类，比较简单

本质上就是把各个事件看成独立的，概率分别计算，概率相乘求出条件概率（后验概率）

然后为了防止概率过小，取log，连乘变为连加，即求和

网页上相关的资料很多，这里就不再赘述了，直接上代码：

https://www.bilibili.com/video/BV1g54y1s7At?from=search&seid=7367289862708839015

参考资料：

https://zhuanlan.zhihu.com/p/84651946

代码一，仅为测试读入，并检测数据合法性

 1 import numpy as np
 2 from sklearn.manifold import TSNE
 3 import matplotlib.pyplot as plt
 4 from mpl_toolkits.mplot3d import Axes3D
 5 
 6 
 7 def read(path: str) -> list:
 8     with open(path, "r") as f:
 9         text = f.readlines()
10         D = []
11         for row in text:
12             substr = str.split(str.split(row, "
")[0], ",")
13             X = []
14             for a in substr:
15                 if a == '?':
16                     continue
17                 X.append(int(a))
18             D.append(X)
19     return D
20 
21 
22 def init(D: list) -> tuple:
23     n, m = len(D), len(D[0])
24     X, Y = [], []
25     for i in range(n):
26         x = []
27         if len(D[i]) != m:
28             n -= 1
29             continue
30         for j in range(1, m - 1, 1):
31             x.append(D[i][j])
32         X.append(x)
33         Y.append(D[i][m - 1])
34     # print(n, m)
35     return X, Y, n, m - 2
36 
37 
38 if __name__ == '__main__':
39 
40     D = read("breast-cancer-wisconsin.data")
41     X, Y, n, m = init(D)
42 
43     x = np.array(X)
44 
45     tsne = TSNE(n_components=3)
46 
47     tsne.fit_transform(x)
48 
49     one_x, one_y, one_z, zero_x, zero_y, zero_z = [], [], [], [], [], []
50     for i in range(n):
51         _x, _y, _z = tsne.embedding_[i][0], tsne.embedding_[i][1], tsne.embedding_[i][2]
52         if Y[i] == 4:
53             zero_x.append(_x)
54             zero_y.append(_y)
55             zero_z.append(_z)
56         else:
57             one_x.append(_x)
58             one_y.append(_y)
59             one_z.append(_z)
60     '''
61     ax = plt.axes(projection='3d')
62     ax.scatter3D(one_x, one_y, one_z)
63     ax.scatter3D(zero_x, zero_y, zero_z)
64     '''
65     plt.subplot(311)
66     plt.scatter(one_x, one_y)
67     plt.scatter(zero_x, zero_y)
68     plt.subplot(312)
69     plt.scatter(one_x, one_z)
70     plt.scatter(zero_x, zero_z)
71     plt.subplot(313)
72     plt.scatter(one_y, one_z)
73     plt.scatter(zero_y, zero_z)
74 
75     plt.show()

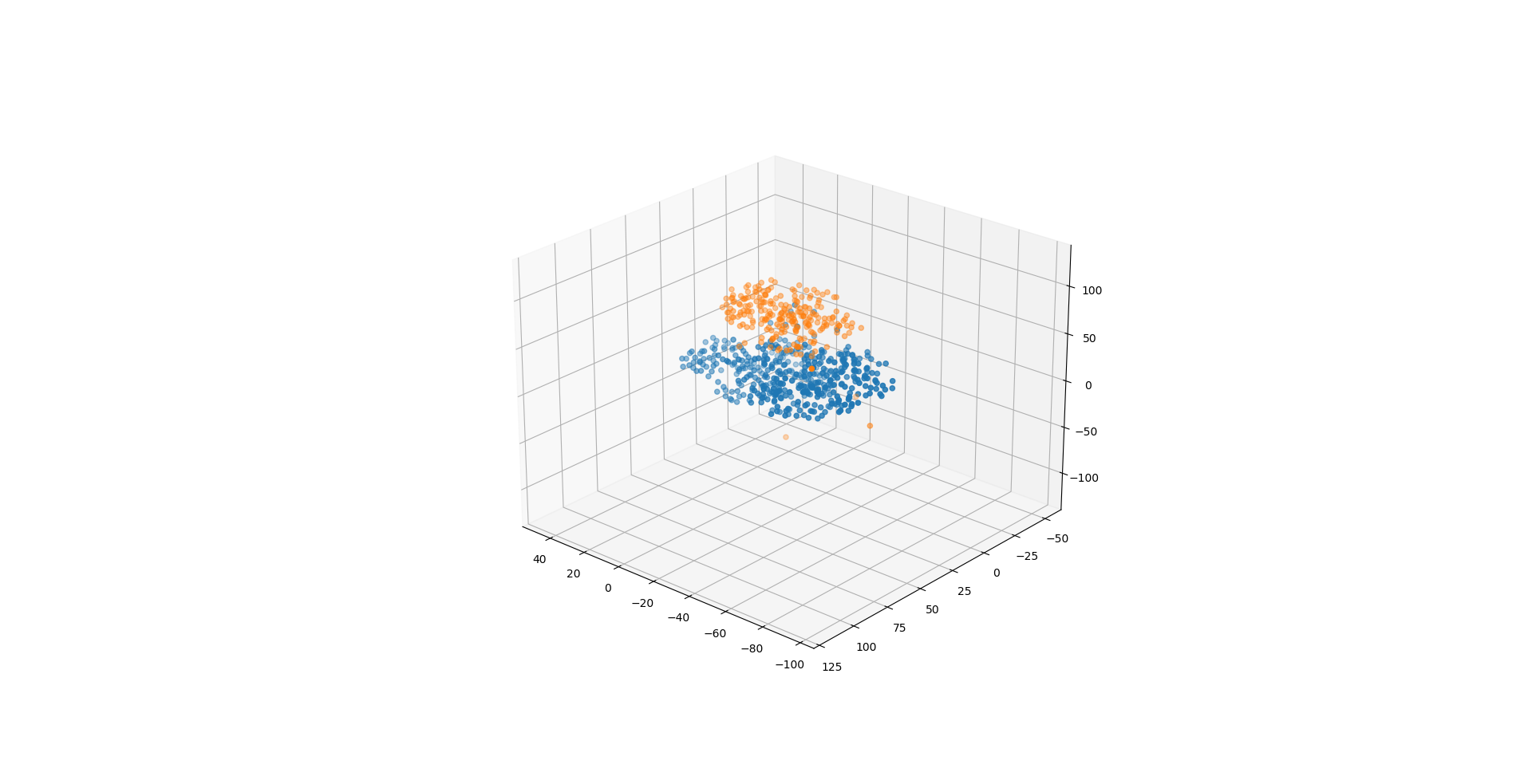
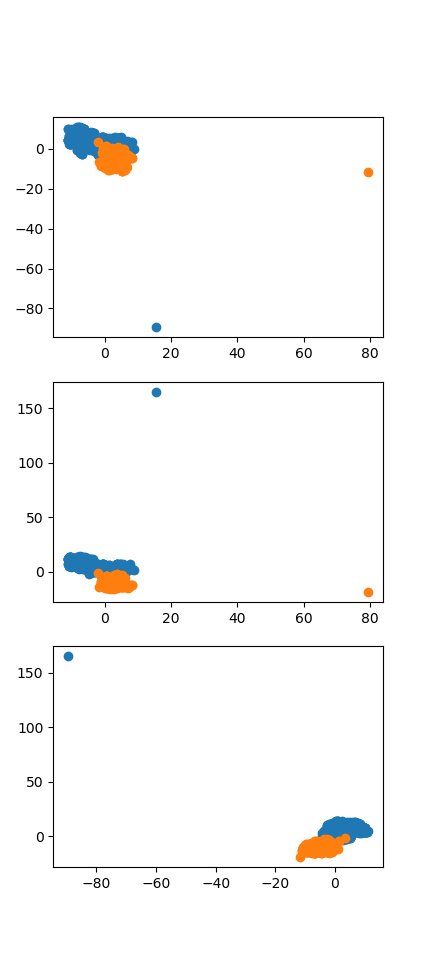
没有划分测试集和数据集，有过拟合之嫌。

准确率accuracy=93.26500732064422%

以下为完整代码：

  1 import numpy as np
  2 from sklearn.manifold import TSNE
  3 import matplotlib.pyplot as plt
  4 from mpl_toolkits.mplot3d import Axes3D
  5 from collections import Counter
  6 
  7 
  8 def read(path: str) -> list:
  9     with open(path, "r") as f:
 10         text = f.readlines()
 11         D = []
 12         for row in text:
 13             substr = str.split(str.split(row, "
")[0], ",")
 14             X = []
 15             for a in substr:
 16                 if a == '?':
 17                     continue
 18                 X.append(int(a))
 19             D.append(X)
 20     return D
 21 
 22 
 23 def init(D: list) -> tuple:
 24     n, m = len(D), len(D[0])
 25     X, Y = [], []
 26     for i in range(n):
 27         x = []
 28         if len(D[i]) != m:
 29             n -= 1
 30             continue
 31         for j in range(1, m - 1, 1):
 32             x.append(D[i][j])
 33         X.append(x)
 34         Y.append(D[i][m - 1])
 35     # print(n, m - 2)
 36     return X, Y, n, m - 2
 37 
 38 
 39 def showDataset(D):
 40     X, Y, n, m = init(D)
 41     x = np.array(X)
 42     tsne = TSNE(n_components=3)
 43 
 44     tsne.fit_transform(x)
 45 
 46     one_x, one_y, one_z, zero_x, zero_y, zero_z = [], [], [], [], [], []
 47     for i in range(n):
 48         _x, _y, _z = tsne.embedding_[i][0], tsne.embedding_[i][1], tsne.embedding_[i][2]
 49         if Y[i] == 4:
 50             zero_x.append(_x)
 51             zero_y.append(_y)
 52             zero_z.append(_z)
 53         else:
 54             one_x.append(_x)
 55             one_y.append(_y)
 56             one_z.append(_z)
 57 
 58     ax = plt.axes(projection='3d')
 59     ax.scatter3D(one_x, one_y, one_z)
 60     ax.scatter3D(zero_x, zero_y, zero_z)
 61     '''
 62     plt.subplot(311)
 63     plt.scatter(one_x, one_y)
 64     plt.scatter(zero_x, zero_y)
 65     plt.subplot(312)
 66     plt.scatter(one_x, one_z)
 67     plt.scatter(zero_x, zero_z)
 68     plt.subplot(313)
 69     plt.scatter(one_y, one_z)
 70     plt.scatter(zero_y, zero_z)
 71     '''
 72     plt.show()
 73 
 74 
 75 # only binary dividing
 76 def multinomialNaiveBayes(X: list, Y: list, n: int, m: int) -> tuple:
 77     X_Positive, X_Negative = [], []
 78     for i in range(n):
 79         if Y[i] > 0:
 80             X_Positive.append(X[i])
 81         else:
 82             X_Negative.append(X[i])
 83     n_Positive = len(X_Positive)
 84     n_Negative = len(X_Negative)
 85     features_Positive = []
 86     features_Negative = []
 87     for j in range(m):
 88         features_Positive.append(comparingFeatureValue(X_Positive, j, n_Positive))
 89         features_Negative.append(comparingFeatureValue(X_Negative, j, n_Negative))
 90     return features_Positive, features_Negative
 91 
 92 
 93 def comparingFeatureValue(X: list, j: int, n: int) -> tuple:
 94     x = [X[i][j] for i in range(n)]
 95     dic_x = Counter(x)
 96     set_x = set(x)
 97     possibility_List = [(label, np.log(dic_x[label] / n)) for label in set_x]
 98     dic_Possibility = dict(possibility_List)
 99     return dic_Possibility, set_x
100 
101 
102 def predict(features_Positive, features_Negative, X, Y, n, m):
103     y = []
104     for i in range(n):
105         x = X[i]
106         possibility_Positive = np.log(len(features_Positive) / n)
107         possibility_Negative = np.log(len(features_Negative) / n)
108         for j in range(m):
109             label = x[j]
110             if label in features_Positive[j][0]:
111                 possibility_Positive += features_Positive[j][0].get(label)
112             if label in features_Negative[j][0]:
113                 possibility_Negative += features_Negative[j][0].get(label)
114         if possibility_Positive > possibility_Negative:
115             y.append(1)
116         else:
117             y.append(-1)
118     accuracy = len([i for i in range(n) if Y[i] == y[i]]) / n
119     return accuracy, y
120 
121 
122 if __name__ == '__main__':
123     D = read("breast-cancer-wisconsin.data")
124     # showDataset(D)
125     X, Y, n, m = init(D)
126     y = [3 - y for y in Y]
127     features_Positive, features_Negative = multinomialNaiveBayes(X, y, n, m)
128     accuracy, y_predict = predict(features_Positive, features_Negative, X, y, n, m)
129     for i in range(n):
130         print("No. {}".format(i + 1))
131         print(X[i])
132         print("real Class:", Y[i])
133         print("predict:", y_predict[i])
134         print("Judging:", ((3 - Y[i]) == y_predict[i]))
135         print()
136     print("accuracy={}%".format(accuracy * 100))

~~Jason_liu O(∩_∩)O

相关阅读:
&&和||解析
 SQL-union union all
sql杂记
 JAVA杂记
 sql之left join、right join、inner join的区别
 蓝鲸邮箱配置
 快速部署社区版（详解）
蓝鲸平台安装环境准备
 蓝鲸脚本集合
 zabbix3.4 install
原文地址：https://www.cnblogs.com/JasonCow/p/14793290.html

INT104-lab10 测试新数据集 完成！[Multinomial Naive Bayes][MLE极大似然估计][二分类]

INT104-lab10 测试新数据集完成！[Multinomial Naive Bayes][MLE极大似然估计][二分类]