Importance Weighted Adversarial Nets for Partial Domain Adaptation学习笔记
Abstract
本文提出了一种基于重要性加权对抗网络的无监督域自适应方法,特别适用于部分域自适应,其中目标领域比源领域拥有更少的类别。
introduce
作者假设目标域的样本均未标注,而且目标域所有的类别都能在源域中找到,即目标域的类别空间是源域类别空间的子集。但是这时候如果直接进行迁移无法有效减小两个域之间的域偏移,因为两个域的标签空间不同,所以域之间的边缘分布本质上也不相同。
在这种情况下,从源域迁移到目标域的一种可行的方式是在分布匹配过程中对于可能出现在目标域的源域类别,对属于该类别的源域样本进行重新加权。然而,目标域是未标注的,揭示哪些类被呈现以及哪些源域样本对于迁移任务是重要的并不简单。针对这一问题,本文提出了一种基于加权对抗网络的深度域适应方法。
基于加权对抗网络的深度域适应方法中包括一个特征提取器以及一个域分类器。其中特域分类器旨在识别源域样本和目标域样本分布之间的差异,以找到真实领域分布散度的更紧密的下界;而特征提取器通过向与域分类器相反的方向步进来减少分布的发散。
本文提出使用使用两个域分类器来获得源域样本的重要程度得分。形象地说,在给定任意一个特征提取器的时候,第一个域分类器输出的最优参数给出了样本来自源域的概率,如果第一个域分类器的激活很大,那么这时候的样本很可能属于两个域共享类别之外的类别。因此,使用第一个域分类器的激活作为每个源域样本对目标域重要性的指示。然后,将所学习的权重应用于源域样本,并且将加权的源域样本和目标域样本送到第二个域分类器,用于优化特征提取器。
作者已经表明,特征提取器和第二个域分类器之间的最小最大博弈在理论上等价于减少加权源密度和目标密度之间的詹森-香农散度。
related work
减小域间差异的方法目前主要有三种:
- 基于统计矩匹配的方法: maximum mean discrepancy (MMD)、Central Moment Discrepancy (CMD)
- 基于对抗损失的方法:鼓励来自不同领域的样本对领域标签不加区分
- 基于正则化的方法:将源域和目标域样本的分布对齐
然而,所有这些方法都依赖于特征空间中边缘分布的匹配,因此为了进行可行的适应,域之间的标签空间都被假定为相同的。
Proposed Method
源域的样本集定义为(X_sin mathbb{R}^{D imes n_s}),源域样本的分布为(P_s(x));目标域的样本集定义为(X_tin mathbb{R}^{D imes n_t}),目标域域样本的分布为(P_t(x))。D表示数据的维度,(n_s)与(n_t)分别表示两个域的样本数量。
源域表示为(D_s={(x^s_i,y^s_i)_{i=1}^{n_s}},x^s_iin mathbb{R}^D)目标域表示为(D_t={(x^t_j)^{n_t}_{j=1}},x^t_j in mathbb{R}^D).
源域与目标域的特征空间假设一致:(mathcal{X}_s=mathcal{X}_t),目标域标签空间是源域标签空间的子集:(mathcal{Y}_t sube mathcal{Y}_s)。
framework
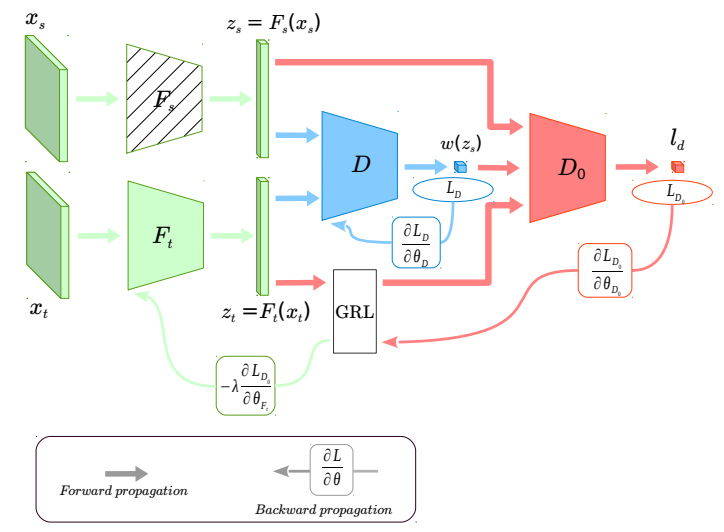
绿色部分是源域与目标域的特征提取器。图中阴影部分表示参数经过了预训练,在训练过程中不会更新。蓝色部分表示第一个域分类器,来获得源域样本的重要性权重。红色部分表示第二个域分类器,用来与带权重的源域样本、目标域样本进行minimax game。GRL表示梯度反转层,在后向传播中改变梯度的符号。
Adversarial Nets-based Domain Adaptation
作者使用了类似论文《Unsupervised domain adaptation by backpropagation》、《Adversarial discriminative domain adaptation》中的前馈网络中域分类器,同时学习区分类别的特征和域不变特征,其中源域数据的标签预测器的损失最小,而域分类器的损失最大。
本文中基于对抗网络的域适应框架与传统GAN相似:
L表示源域样本分类的损失。
给定训练后的(F_s(x)),使用域对抗损失,通过优化(F_t(x))与D来减小域间差异。
其中(F_t)的参数使用(F_s)完成初始化。
在给定(F_s(x))(类比对应原始GAN模型中的真实图片)以及(F_t(x))(类比对应GAN模型中的生成图片),最合适的D为:
其中(z=F(x))表示经过特征提取器提取特征后特征空间中的样本。
Importance Weighted Adversarial Nets-based Domain Adaptation
Sample weights learning
在公式(3)中,域分类器为(D(z)=p(y=1|z)=sigma(a(z))),其中(sigma)表示sigmoid激活函数。假设域分类器已经收敛到对于当前特征提取器而言的最优值,则域分类器的输出表示样本来自源域分布的可能性。
- 如果(D^*(z)approx 1),表示样本很可能来自源域中共享类别之外的类别,因为覆盖样本的区域几乎没有或根本没有目标样本,并且可以通过域分类器几乎完美地与目标域样本分布区分开来。这些样本将被域分类器以及特征提取器忽略。
- 如果(D^*(z))很小,则样本更可能来自两个域的共享类别,这些样本应该被赋予更大的重要性权重,以减少共享类间的域偏移。
因此,权重函数应该与(D^*(z))成反比,定义源域样本的重要性权重函数:
于是源域共享类别之外的样本的重要性权重函数的值就小于共享类别中样本的重要性权重函数值。权重函数也是源域和目标域特征之间的密度比的函数,这进一步验证了权重函数的合理性,因为覆盖很少或没有目标样本的样本的邻近区域将被分配小的权重。
作者的目的是获得源域样本的相对重要性,建议来自非共享类别的样本应该被赋予比来自共享类别的样本相对更小的权重。因此,权重标准化如下:
其中(mathbb{E}_{zsim p_s(z)}{w}(z)=1)
权重函数属于域分类器的函数,如果在同一个的域分类器上应用权重,则minimax game的理论结果将不会减少两个密度之间的JensenShannon散度(因为由于引入了权重函数(也是D的函数),所以最佳分类器(例如等式4)将不会是源密度与源和目标密度之和之间的比率)。
于是作者在提取后的特征上使用第二个域分类器进行加权后源域样本与目标域样本的比较。这样一来,第一个域分类器只是基于(F_s)与(F_t)得到源域样本的重要性权重,则域分类器D在后向传播时不会更新(F_t)的参数。因为D的梯度是在未加权的源域样本上学习的,并且不是减少共享类别上的域偏移的好指标,所以作者使用第二个域分类器(D_0)来进行minimax game,更新(F_t),减小共享类别之间的差异。
将重要性权重添加到源域样本中后,加权对抗网络的目标函数为:
其中(w(z))为域分类器D的函数,对于(D_0)来说知识一个常数。所以,给定(F_s)与D,对于任意一个(F_t),(D_0)的最优结果为:
可是(w(z)p_s(z))仍然是一个概率密度函数,于是作者将公式(9)中的minimax game改写为
因此,基于加权对抗网的域自适应本质上是减少特征空间中加权源密度和目标密度之间的詹森-香农散度,从而在(w(z)p_s(z) = p_t(z))上获得最优。
Target data structure preservation
如果特征空间中加权的源域分布和目标域分布之间的偏移很小,则从源域样本中学习的分类器C可以直接用于目标域。在这里,我们通过使用熵最小化原则进一步约束(F_t),以鼓励类之间的低密度分离: