自编码器
简介
神经网络就是一种特殊的自编码器,区别在于自编码器的输出和输入是相同的,是一个自监督的过程,通过训练自编码器,得到每一层中的权重参数,自然地我们就得到了输入x的不同的表示(每一层代表一种)这些就是特征,自动编码器就是一种尽可能复现原数据的神经网络。
自编码器通过简单地学习将输入复制到输出来工作。这一任务(就是输入训练数据, 再输出训练数据的任务)听起来似乎微不足道,但通过不同方式对神经网络增加约束,可以使这一任务变得极其困难。比如,可以限制内部表示的尺寸(这就实现降维了),或者对训练数据增加噪声并训练自编码器使其能恢复原有。这些限制条件防止自编码器机械地将输入复制到输出,并强制它学习数据的高效表示。简而言之,编码(就是输入数据的高效表示)是自编码器在一些限制条件下学习恒等函数(identity function)的副产品。
特点
跟数据相关程度很高,这意味着自动编码器只能压缩与训练数据相似的数据,因为使用神经网络提取的特征一般是高度相关于原始的训练集。
压缩后数据是有损的,这是因为降维的过程中不可避免地丢失信息,解压之后的输出和原始的输入相比是退化的。
应用
数据去噪,进行可视化降维。生成数据。
结构
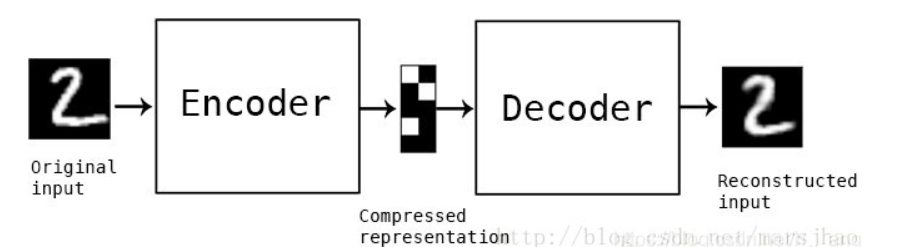
通常使用神经网络作为编码器和解码器,输入的数据经过神经网络降维到一个编码(code),接着又通过另外一个神经网络去解码得到一个与输入原数据一模一样的生成数据,然后通过比较这两个数据,最小化它们之间的差异来训练这个网络中编码器和解码器的参数。
分层训练方法
多层的训练方法:先进行第一层的code的训练,我们将第一层输出的code当成第二层的输入信号,同样最小化重构误差,就会得到第二层的参数,并且得到第二层输出的code,也就是原输入信息的第二个表达了。其他层就同样的方法炮制就行了
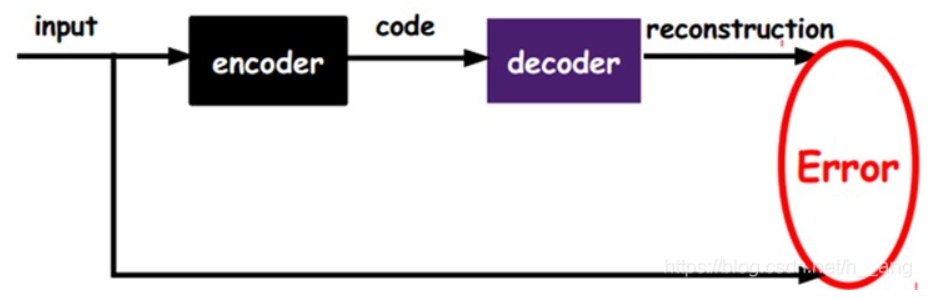
当input的维度大于code的维度的时候,表示该变换是一种降维的操作
当input的维度小于code的维度的时候,即稀疏编码器
香草自编码器
香草自编码器(Vanilla Autoencoder),只有三层网络,即只有一个隐藏层的神经网络。它的输入和输出是相同的,可通过使用Adam优化器和均方误差损失函数,来学习如何重构输入。
隐藏层的压缩维度为32,小于输入维度784,因此这个编码器是有损的,通过这个约束,来迫使神经网络来学习数据的压缩表征。
栈式自编码器
和其他的神经网络一样,自编码器可以有多个隐层,这被称作栈式自编码器(或者深度自编码器)。增加隐层可以学到更复杂的编码,但千万不能使自编码器过于强大。
栈式自编码器的架构一般是关于中间隐层对称的。
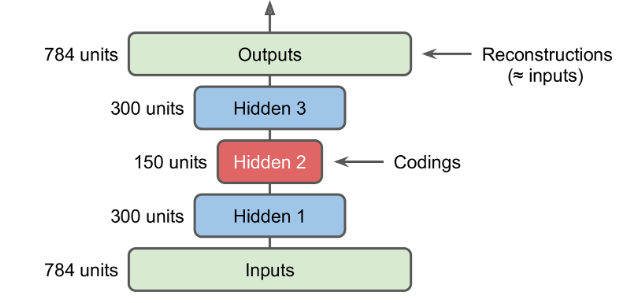
1.捆绑权重
如果一个自编码器的层次是严格轴对称的,一个常用的技术是将decoder层的权重捆绑到encoder层。这使得模型参数减半,加快了训练速度并降低了过拟合风险
2.一次训练一个自编码器
与之前训练整个栈式自编码器不同,可以训练多个浅层的自编码器,然后再将它们合并为一体,这样要快得多。
例如:第一个自编码器学习去重建输入。然后,第二个自编码器学习去重建第一个自编码器隐层的输出。最后,这两个自编码器被整合到一起,如图15-4。可以使用这种方式,创建一个很深的栈式自编码器。
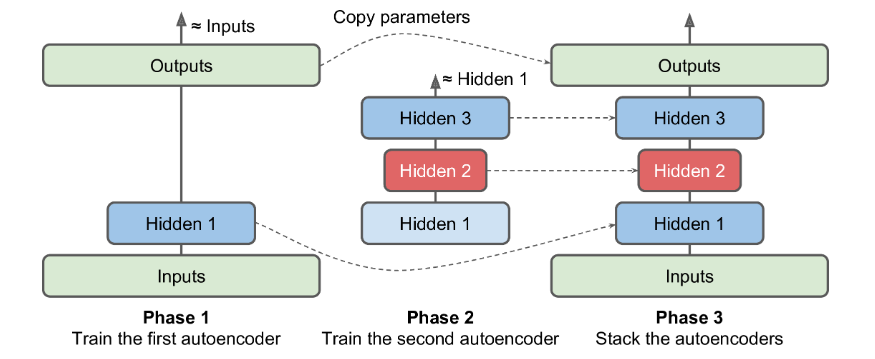
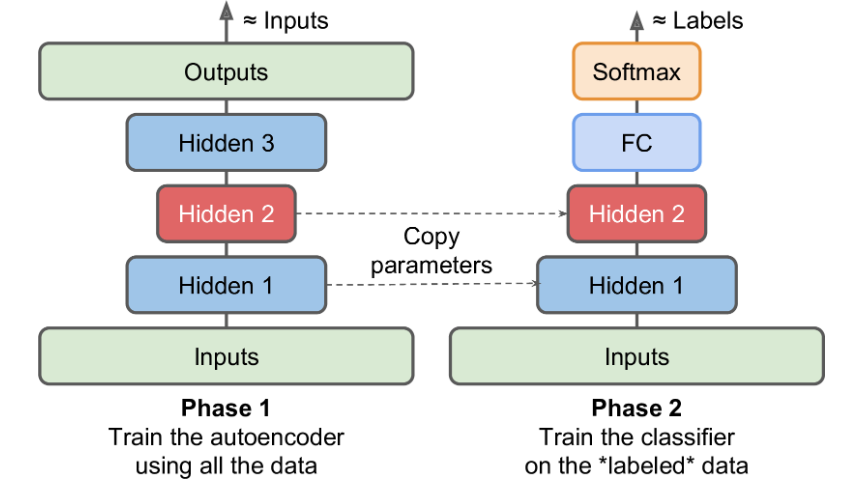
3.进行无监督预训练
如果有一个很大的数据集但绝大部分是未标注数据,可以使用所有的数据先训练一个栈式自编码器,然后复用低层来完成真正的任务。
去噪自编码器
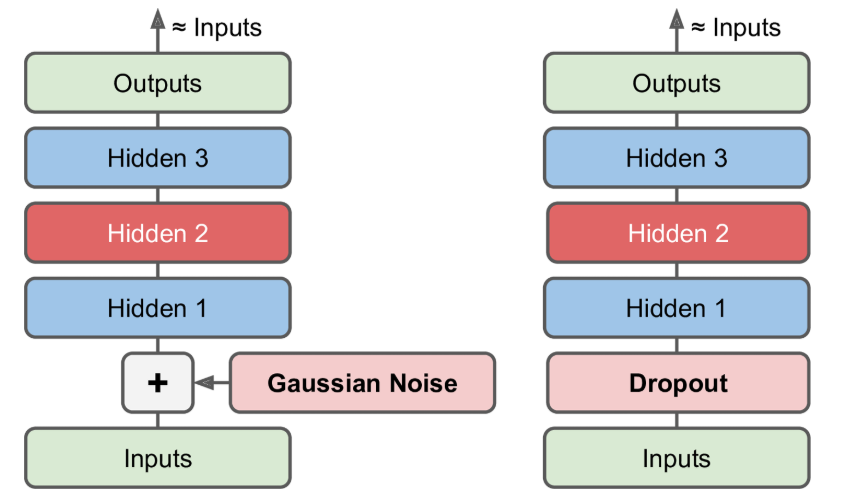
制自编码器学习有用特征的方式是在输入增加噪声,通过训练之后得到无噪声的输出。这防止了自编码器简单的将输入复制到输出,从而提取出数据中有用的模式
噪声可以是添加到输入的纯高斯噪声,也可以是随机丢弃输入层的某个特征,类似于dropout。
变分自编码器
我们想利用现有的样本去生成一些新的样本,从而扩大数据量。如果我们能知道原始数据集x的分布p(x),那么我们直接从这个分布中采样就可以得到新的样本。而在现实中,我们无法得到数据集的真实分布,于是变分编码器利用了一个隐分布z,通过z来生成新的样本,从概率角度来说就是p(x) = p(z)×p(x|z)。通过构造隐变量,让我们可以近似等于从原始分布中采样来组成新样本,而效果的好坏就靠模型来实现了。
首先想到的是用神经网络来训练参数,那么当训练好模型后,我们输入x,可以生成新的样本x’,且他们近似都是从原始数据集分布中采样出来的,故可以参与训练其他模型,也就完成了数据增强。那么第一个损失函数就应运而生,即比较生成的x’和原始样本x的差距,差距越小效果越好。
但是这样自然是不可行的,因为既然训练的目的是使输出样本和原样本相似度最高,那么我们直接拷贝一份原数据就行了,就不需要训练了。也就是说,数据增强的目的不仅要保证增强的数据都服从和源数据一样的分布,而且要有多样性,即有一些源数据没有的特征,这样才能达到数据增强的目的。
于是我们考虑采样,因为采样的数据服从同一分布,但又各不相同,就可以满足多样性这一要求。
考虑从隐分布z来进行数据采样,一个很自然的想法就是采用标准正态分布,但是如果对于所有的样本,训练的时候我们都从z中进行采样,然后用于训练,那么也就和原始的输入数据没什么关系了,即采样出的z不知道是由哪一个原始数据x生成的,这样也就没法进行损失计算,也就没法训练神经网络了。于是考虑如何把生成的数据和原始数据能一一对应起来,变分编码器让每个样本都服从一个正态分布,但这个正态分布又各不相同,即正态分布的两个参数均值和方差各不相同,那么这样输入输出就可以一一对应了。
那么如何学习输入的每个样本服从的正态分布的均值和方差呢,这个时候就要用到神经网络了,一切不好计算的都用神经网络去拟合,于是对于每个输入样本经过一层或多层神经网络,分别输出均值和方差,然后再从服从此均值和方差的正态分布中去随机采样生成新的样本。
看似已经可以完成数据增强的目的了,但是仔细想想问题还有很多。首先既然损失函数是输出样本和输入样本的相似度,那么网络肯定往减少输出样本和输入样本的差异上去拟合,我们记得输出样本是通过在正态分布上采样得到的,我们知道正态分布的方差越大,则数据越分散,采样得到的数据噪声越大,导致输出样本和输入样本的相似度很小,于是网络训练会尽量减小正态分布的方差,直到接近0,那么还是那个问题,方差接近0,则生成的数据的多样性又减少了。所以这个问题还是没有解决。
变分编码器使神经网络学到的正态分布尽量趋近于标准正态分布,即学到的均值和方差分别趋近于0和1。如何做到呢,那就是再增加一个损失函数。增加的损失函数是衡量网络学习到的正态分布和标准正态分布的差异性,即使用了KL散度。这样,神经网路一方面要学习输入输出的相似性,还要考虑增加一定的噪音,即不使正态分布的方差趋紧于0,也就增加了输出的多样性。


参考: