P1364 医院设置 【带权值的树的重心】

题目

https://www.luogu.com.cn/problem/P1364

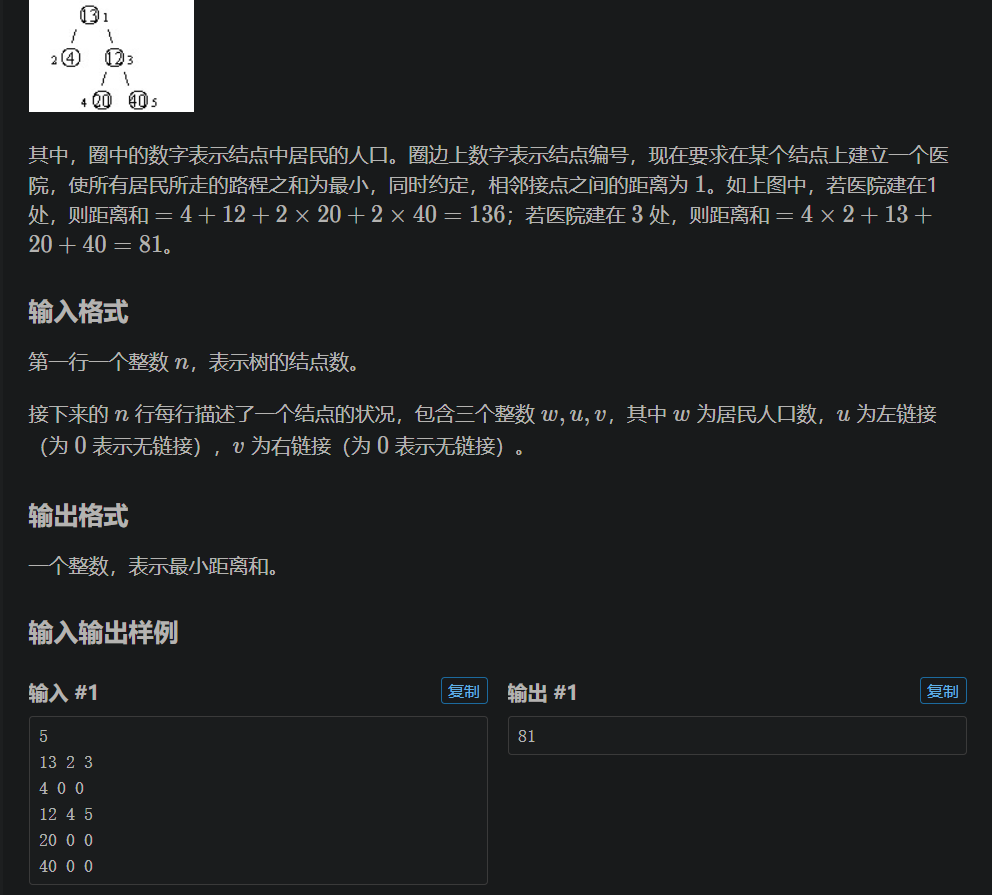
 思路

该题是典型的找树的重心的题型，但是特殊的是它是一个带权树的重心。

 它是首先初始化一个f，即一个点到其它点的距离，这里为了方便就直接初始化了1号节点，之后在dp函数中来计算其他节点的f值

当根从u变为v的时候，v的子树的所有节点原本的距离要到u，现在只要到v了，每个结点的距离都减少1，那么总距离就减少size[v]，

同时，以v为根的子树以外的所有节点，原本只要到u就行了，现在要到v，每个节点的路程都增加了1

总路程就增加size[1]−size[v]，其中size[1]就是我们预处理出来的整棵树的大小，减去size[v]就是除以v为根的子树以外的结点数。

 代码

#include<iostream>
#include<cstdio>
#include<string>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
#define maxn 200
#define maxm 5000
struct edge
{
    int to;
    int next;
}e[maxm*2];
int head[maxn], vis[maxn],amount[maxn], num[maxn],f[maxn],cnt = 0;
int n, minn = 999999;
void addedge(int u,int v)
{
    cnt++;
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
}

void dfs(int p, int fa,int depth)
{
    num[p] = amount[p];
    for (int i = head[p]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (y == fa)continue;
        dfs(y, p,depth+1);
        num[p] += num[y];
    }
    f[1] += amount[p] * depth;
}

void dp(int p, int fa)
{
    for (int i = head[p]; i; i = e[i].next)
    {
        int y = e[i].to;
        if (y == fa)continue;
        f[y] = f[p] + num[1] - num[y] * 2;
        dp(y, p);
    }
    minn = min(minn, f[p]);

}


int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        int w, u, v;
        scanf("%d%d%d", &w, &u, &v);
        amount[i] = w;
        if (u != 0)
        {
            addedge(i, u);
            addedge(u, i);
        }
        if (v != 0)
        {
            addedge(i, v);
            addedge(v, i);
        }
    }
    dfs(1, 0,0);
    dp(1, 0);
    printf("%d", minn);

}