本文通过利用信用卡的历史交易数据进行机器学习,构建信用卡反欺诈预测模型,对客户信用卡盗刷进行预测
一、项目背景
对信用卡盗刷事情进行预测对于挽救客户、银行损失意义十分重大,此项目数据集来源于Kaggle,数据集包含由欧洲持卡人于2013年9月使用信用卡进行交的数据。此数据集显示两天内发生的交易,其中284,807笔交易中有492笔被盗刷。数据集非常不平衡,积极的类(被盗刷)占所有交易的0.172%。因判定信用卡持卡人信用卡是否会被盗刷为二分类问题,解决分类问题我们可以有逻辑回归、SVM、随机森林算法,也可利用boost集成学习的XGboost算法进行数据的训练与判别,本文中采用逻辑回归算法进行测试。
二、探索性数据分析
2.1 理解数据
import numpy as np
import pandas as pd
import sklearn as skl
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import gridspec
import warnings
warnings.filterwarnings("ignore")
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, precision_recall_curve, auc, roc_auc_score, roc_curve, recall_score, classification_report
from sklearn.linear_model import LogisticRegression
data = pd.read_csv('../input/creditcard.csv')
data.info()
data.head()
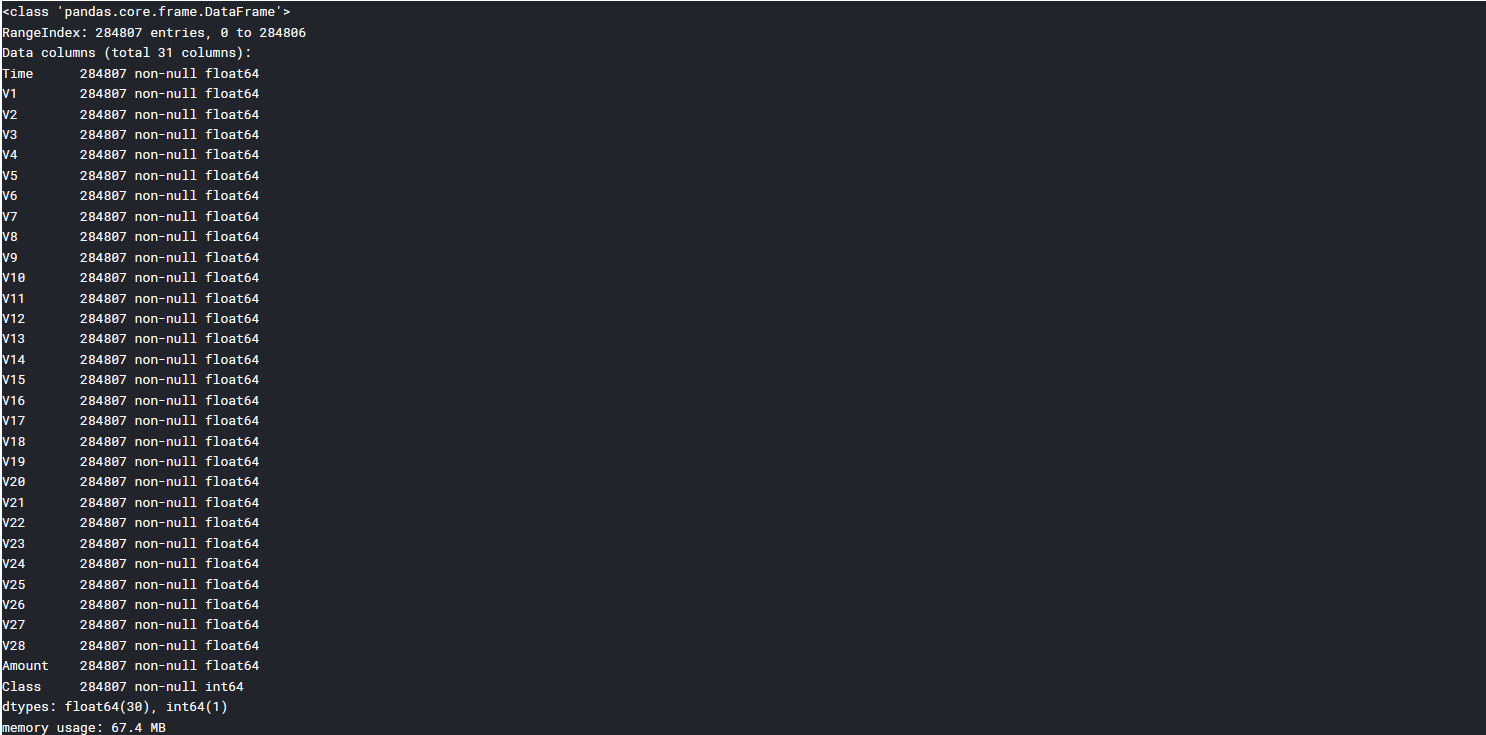

可见数据共有31列,284807行,其中V1-V28为结构化数据,另一列为整形数据,也为类别属性Class,Amount和Time的数据特征与规格与其他特征不大相同。
2.2 数据初步探索
print('No Frauds', round(data['Class'].value_counts()[0]/len(data) * 100,2), '% of the dataset')
print('Frauds', round(data['Class'].value_counts()[1]/len(data) * 100,2), '% of the dataset')
colors = ["#0101DF", "#DF0101"]
sns.countplot('Class', data=data, palette=colors)
plt.title('Class Distributions
(0: No Fraud || 1: Fraud)', fontsize=14)
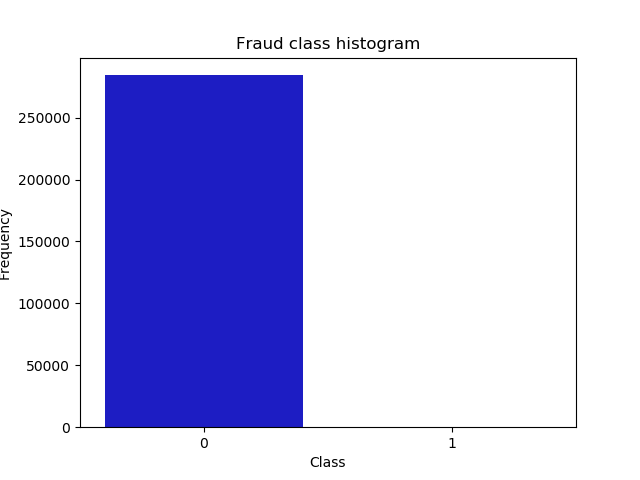
No Frauds 99.83 % of the dataset
Frauds 0.17 % of the dataset
可以看出数据很不均衡:数据不均衡很可能导致我们模型预测结果‘0’时很准确,而预测‘1’时并不准确。
2.3 数据预处理
由上图知Fraud 与No Fraud的数据不均衡,若直接进行数据建模则会造成如下问题:
1)过拟合,因样本中存在大量的正例(No Fraud),故机器可能过多学习正例的特征而造成判断错误
2)特征关联错误,因样本数据不平衡,容易将不同的特征属性误关联
解决方案有如下:
1)Random undersampling,欠采样
通过选取正例中与Fraud相同数量的样本构成均衡的样本,这样新的样本样本中,Fraud、No Fraud各占50%
2)Oversampling,过采样
采用SMOTE算法,从少数类Fraud中创建合成点,以便在少数类和多数类之间达到平衡,不必删除任何行,这与随机欠采样不同,也由于没有如前所述未删除任何行,因此需要更多时间进行训练
需要说明的是虽然我们在实现Random Undersampling或Oversampling技术时对数据进行处理,但仍需要原始测试集上测试我们的模型,而不是在欠采样或过采样上。欠采样和过采样的作用是使构建的模型合适,最终还是服务于原始数据集。之后对分别采用欠采样和过采样的方法进行数据处理、建模,再对原始数据集进行预测分析。
此外还发现Amount列数值较大,不符合数据相似性原则,因此需要归一化使其范围在(-1, 1),否则在进行皮尔逊相关性分析时会出错。
三、特征工程
1. 绘制各种特征的分布图
1 )查看盗刷与正常刷卡的刷卡金额分布图
f,(ax1,ax2) = plt.subplots(2, 1, sharex=True, figsize=(12,4))
bins=30
ax1.hist(data[data.Class ==1]['Amount'],bins=bins)
ax1.set_title('Fraud')
ax2.hist(data[data.Class == 0]['Amount'], bins=bins)
ax2.set_title('Normal')
plt.xlabel('Amount ($)')
plt.ylabel('Number of Transactions')
plt.yscale('log')
plt.show()
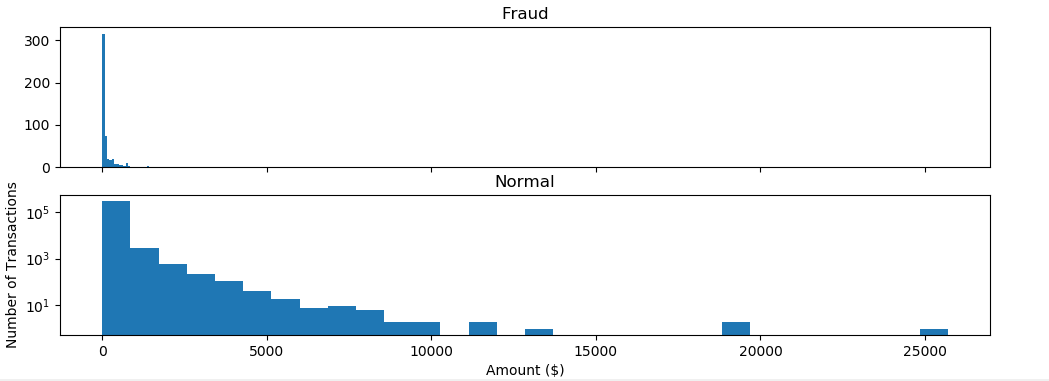
(信用卡被盗刷发生的金额与信用卡正常用户发生的金额相比,比较小。这说明信用卡盗刷者为了不引起信用卡卡主的注意,更偏向选择小金额消费)
2) 查看交易时间与交易金额的分布图
fig, ax = plt.subplots(1, 2, figsize=(18,4))
amount_val = data['Amount'].values
time_val = data['Time'].values
sns.distplot(amount_val, ax=ax[0], color='r')
ax[0].set_title('Distribution of Transaction Amount', fontsize=14)
ax[0].set_xlim([min(amount_val), max(amount_val)])
sns.distplot(time_val, ax=ax[1], color='b')
ax[1].set_title('Distribution of Transaction Time', fontsize=14)
ax[1].set_xlim([min(time_val), max(time_val)])
plt.show()
3) 查看其他特征的分布图
plt.figure(figsize=(12,28*4))
v_features = data.ix[:,1:29].columns
gs = gridspec.GridSpec(28, 1)
for i, cn in enumerate(data[v_features]):
ax = plt.subplot(gs[i])
sns.distplot(data[data.Class == 1][cn], bins=50)
sns.distplot(data[data.Class == 0][cn], bins=50)
ax.set_xlabel('')
ax.set_title('histogram of feature:' + str(cn))
plt.show()

2. 处理不平衡数据
对Amount进行归一化,使其范围在(-1, 1)
from sklearn.preprocessing import StandardScaler
data['normAmount'] = StandardScaler().fit_transform(data['Amount'].reshape(-1, 1))
data = data.drop(['Time','Amount'],axis=1)
此外还需要进行采用处理,分为欠采样处理和过采样处理,Random undersampling 和 Oversampling,这里先按照欠处理采样进行分析。因此我们得到一个正反例平衡的数据样本。
X = data.ix[:, data.columns != 'Class']
y = data.ix[:, data.columns == 'Class']
number_records_fraud = len(data[data.Class == 1])
fraud_indices = np.array(data[data.Class == 1].index)
normal_indices = data[data.Class == 0].index
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)
random_normal_indices = np.array(random_normal_indices)
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])
under_sample_data = data.iloc[under_sample_indices,:]
X_undersample = under_sample_data.ix[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.ix[:, under_sample_data.columns == 'Class']
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 0)
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample ,y_undersample, test_size = 0.3, random_state = 0)
3.相关性特征分析
3.1 相关性分析
f, (ax1, ax2) = plt.subplots(2, 1, figsize=(24,20))
# Entire DataFrame
corr = data.corr()
sns.heatmap(corr, cmap='coolwarm_r', annot_kws={'size':20}, ax=ax1)
ax1.set_title("Imbalanced Correlation Matrix
(don't use for reference)", fontsize=14)
sub_sample_corr = under_sample_data.corr()
sns.heatmap(sub_sample_corr, cmap='coolwarm_r', annot_kws={'size':20}, ax=ax2)
ax2.set_title('SubSample Correlation Matrix
(use for reference)', fontsize=14)
plt.show()
可以看到如不对非平衡数据进行处理,有可能得出错误的相关性结论
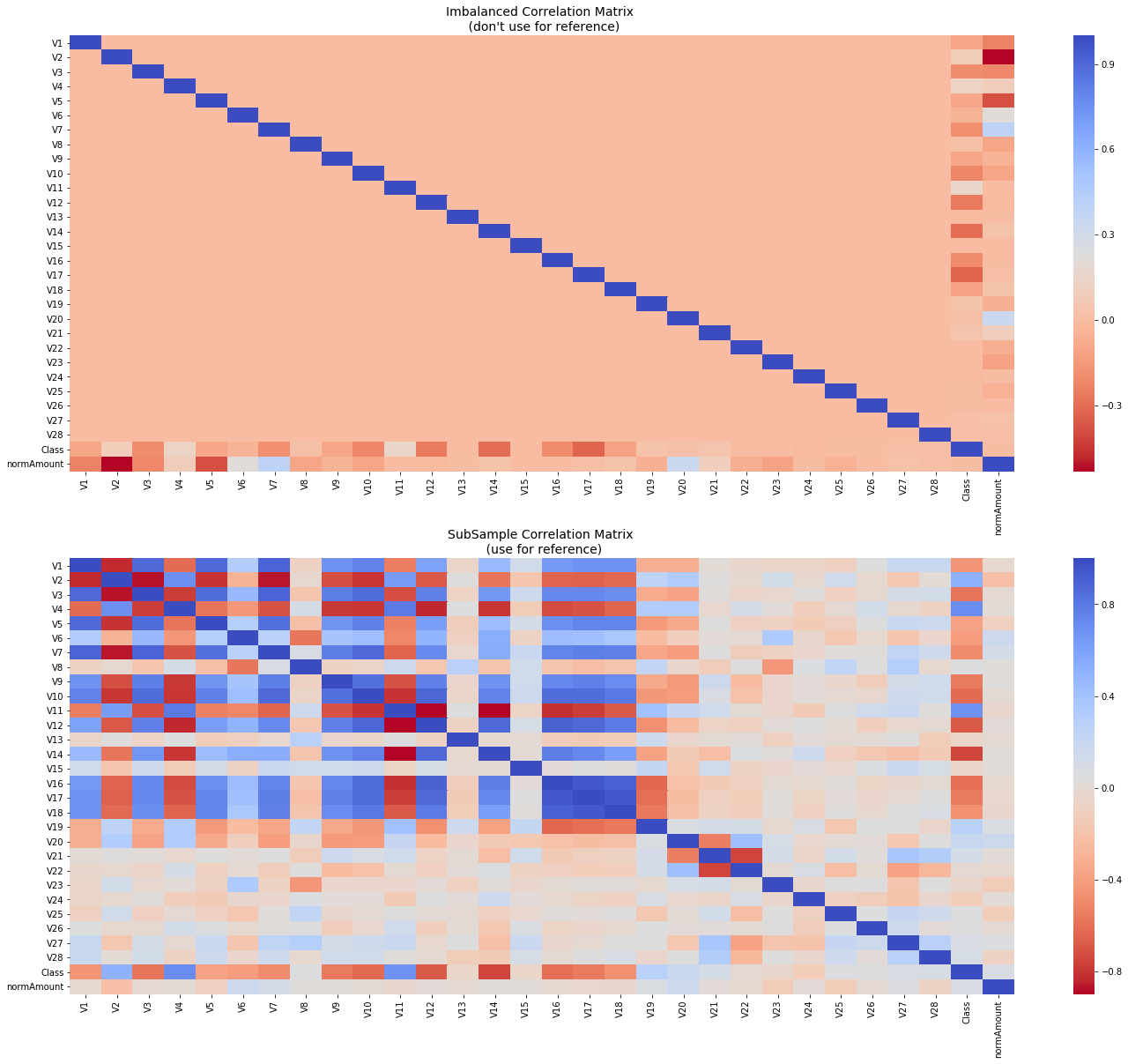
通过heatmap发现,V14,V12和V10呈负相关,这意味着这些值越低,最终结果就越有可能成为欺诈交易,V4,V11和V19正相关。注意这些值越高,最终结果越有可能成为欺诈交易。
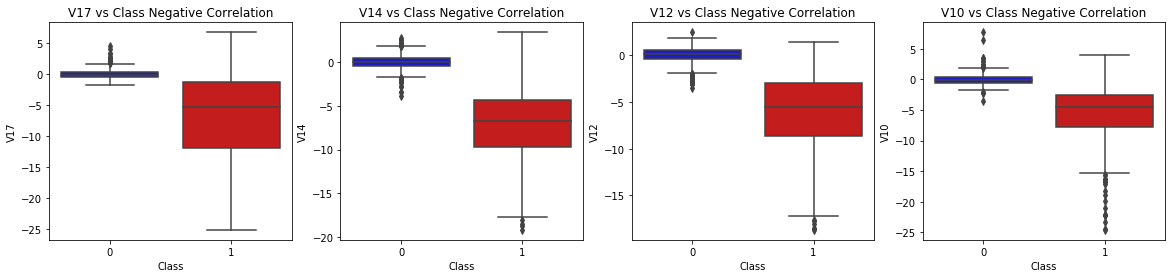
3.2 箱线图
绘制上述的正相关、负相关的特征属性的箱线图
f, axes = plt.subplots(ncols=4, figsize=(20,4))
# Positive correlations (The higher the feature the probability increases that it will be a fraud transaction)
sns.boxplot(x="Class", y="V11", data=under_sample_data, palette=colors, ax=axes[0])
axes[0].set_title('V11 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V4", data=under_sample_data, palette=colors, ax=axes[1])
axes[1].set_title('V4 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V2", data=under_sample_data, palette=colors, ax=axes[2])
axes[2].set_title('V2 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V19", data=under_sample_data, palette=colors, ax=axes[3])
axes[3].set_title('V19 vs Class Positive Correlation')
plt.show()
f, axes = plt.subplots(ncols=4, figsize=(20,4))
# Positive correlations (The higher the feature the probability increases that it will be a fraud transaction)
sns.boxplot(x="Class", y="V11", data=new_df, palette=colors, ax=axes[0])
axes[0].set_title('V11 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V4", data=new_df, palette=colors, ax=axes[1])
axes[1].set_title('V4 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V2", data=new_df, palette=colors, ax=axes[2])
axes[2].set_title('V2 vs Class Positive Correlation')
sns.boxplot(x="Class", y="V19", data=new_df, palette=colors, ax=axes[3])
axes[3].set_title('V19 vs Class Positive Correlation')
plt.show()
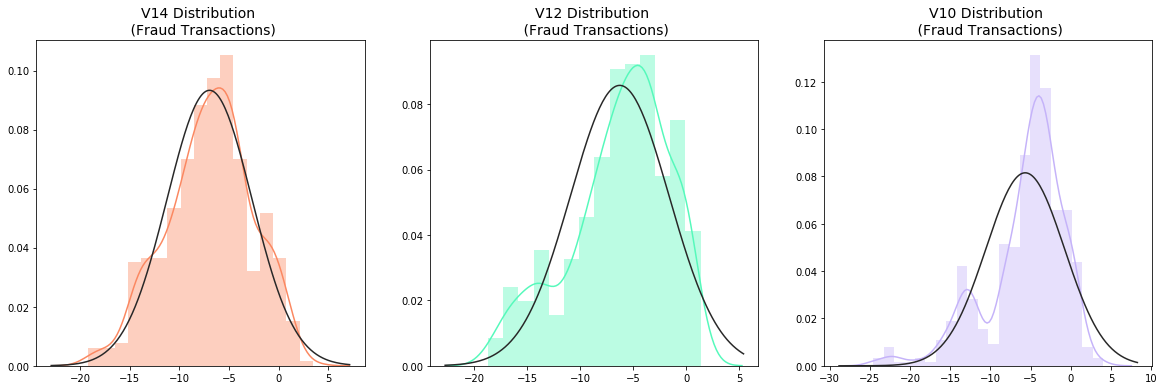
3.3 异常值处理
在异常值处理前,需要可视化我们将要使用的特征的。由于上述V14、V12、V10为负相关特征,观察这些特征的分布,与其他相比,V14是唯一具有高斯分布的特征。根据四分位数确定阀值,对在阀值外的异常数据进行剔除。
from scipy.stats import norm
f, (ax1, ax2, ax3) = plt.subplots(1,4, figsize=(20, 6))
v14_fraud_dist = under_sample_data['V14'].loc[under_sample_data['Class'] == 1].values
sns.distplot(v14_fraud_dist,ax=ax1, fit=norm, color='#FB8861')
ax1.set_title('V14 Distribution
(Fraud Transactions)', fontsize=14)
v12_fraud_dist = under_sample_data['V12'].loc[under_sample_data['Class'] == 1].values
sns.distplot(v12_fraud_dist,ax=ax2, fit=norm, color='#56F9BB')
ax2.set_title('V12 Distribution
(Fraud Transactions)', fontsize=14)
v10_fraud_dist = under_sample_data['V10'].loc[under_sample_data['Class'] == 1].values
sns.distplot(v10_fraud_dist,ax=ax3, fit=norm, color='#C5B3F9')
ax3.set_title('V10 Distribution
(Fraud Transactions)', fontsize=14)
plt.show()
查看特征V14、V12、V10的分布图,选择具有正态分布特征的V14
# -----> V14 Removing Outliers (Highest Negative Correlated with Labels)
v14_fraud = under_sample_data['V14'].loc[under_sample_data['Class'] == 1].values
q25, q75 = np.percentile(v14_fraud, 25), np.percentile(v14_fraud, 75)
print('Quartile 25: {} | Quartile 75: {}'.format(q25, q75))
v14_iqr = q75 - q25
print('iqr: {}'.format(v14_iqr))
v14_cut_off = v14_iqr * 1.5
v14_lower, v14_upper = q25 - v14_cut_off, q75 + v14_cut_off
print('Cut Off: {}'.format(v14_cut_off))
print('V14 Lower: {}'.format(v14_lower))
print('V14 Upper: {}'.format(v14_upper))
outliers = [x for x in v14_fraud if x < v14_lower or x > v14_upper]
print('Feature V14 Outliers for Fraud Cases: {}'.format(len(outliers)))
print('V14 outliers:{}'.format(outliers))
under_sample_data = under_sample_data.drop(under_sample_data[(under_sample_data['V14'] > v14_upper) | (under_sample_data['V14'] < v14_lower)].index)
print('----' * 44)
# -----> V12 removing outliers from fraud transactions
v12_fraud = under_sample_data['V12'].loc[under_sample_data['Class'] == 1].values
q25, q75 = np.percentile(v12_fraud, 25), np.percentile(v12_fraud, 75)
v12_iqr = q75 - q25
v12_cut_off = v12_iqr * 1.5
v12_lower, v12_upper = q25 - v12_cut_off, q75 + v12_cut_off
print('V12 Lower: {}'.format(v12_lower))
print('V12 Upper: {}'.format(v12_upper))
outliers = [x for x in v12_fraud if x < v12_lower or x > v12_upper]
print('V12 outliers: {}'.format(outliers))
print('Feature V12 Outliers for Fraud Cases: {}'.format(len(outliers)))
new_df = under_sample_data.drop(under_sample_data[(under_sample_data['V12'] > v12_upper) | (under_sample_data['V12'] < v12_lower)].index)
print('Number of Instances after outliers removal: {}'.format(len(under_sample_data)))
print('----' * 44)
# Removing outliers V10 Feature
v10_fraud = under_sample_data['V10'].loc[under_sample_data['Class'] == 1].values
q25, q75 = np.percentile(v10_fraud, 25), np.percentile(v10_fraud, 75)
v10_iqr = q75 - q25
v10_cut_off = v10_iqr * 1.5
v10_lower, v10_upper = q25 - v10_cut_off, q75 + v10_cut_off
print('V10 Lower: {}'.format(v10_lower))
print('V10 Upper: {}'.format(v10_upper))
outliers = [x for x in v10_fraud if x < v10_lower or x > v10_upper]
print('V10 outliers: {}'.format(outliers))
print('Feature V10 Outliers for Fraud Cases: {}'.format(len(outliers)))
new_df = under_sample_data.drop(under_sample_data[(under_sample_data['V10'] > v10_upper) | (under_sample_data['V10'] < v10_lower)].index)
print('Number of Instances after outliers removal: {}'.format(len(under_sample_data)))
去除异常值,显示结果如下
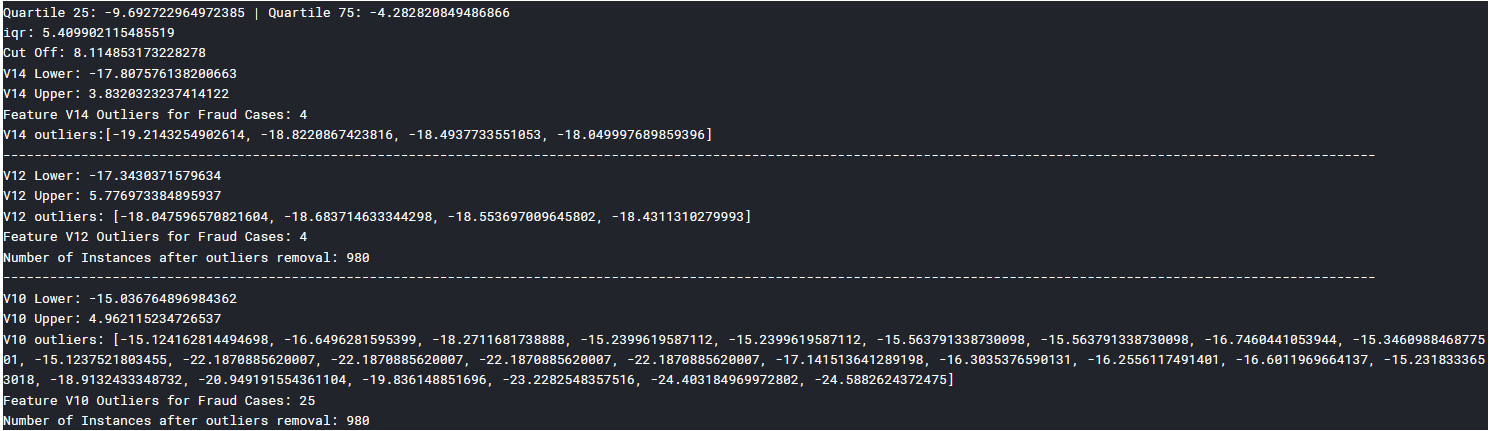
f,(ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20,6))
colors = ['#B3F9C5', '#f9c5b3']
sns.boxplot(x="Class", y="V14", data=under_sample_data,ax=ax1, palette=colors)
ax1.set_title("V14 Feature
Reduction of outliers", fontsize=14)
ax1.annotate('Fewer extreme
outliers', xy=(0.98, -17.5), xytext=(0, -12),
arrowprops=dict(facecolor='black'),
fontsize=14)
sns.boxplot(x="Class", y="V12", data=under_sample_data, ax=ax2, palette=colors)
ax2.set_title("V12 Feature
Reduction of outliers", fontsize=14)
ax2.annotate('Fewer extreme
outliers', xy=(0.98, -17.3), xytext=(0, -12),
arrowprops=dict(facecolor='black'),
fontsize=14)
sns.boxplot(x="Class", y="V10", data=under_sample_data, ax=ax3, palette=colors)
ax3.set_title("V10 Feature
Reduction of outliers", fontsize=14)
ax3.annotate('Fewer extreme
outliers', xy=(0.95, -16.5), xytext=(0, -12),
arrowprops=dict(facecolor='black'),
fontsize=14)
plt.show()
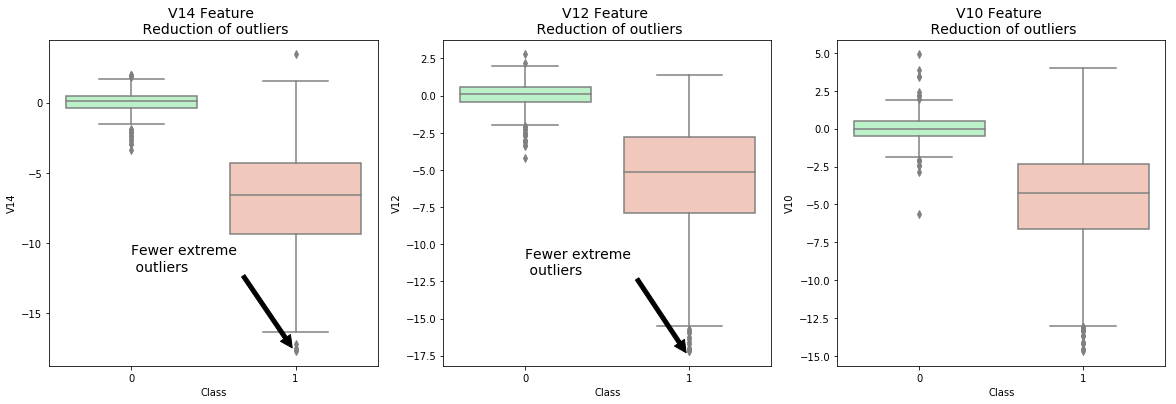
3.3 降维
降维的作用是将高维的数据集中不必要的特征去除,只保留需要的特征属性。此处采用PCA和SVD进行降维分析
import time
from sklearn.decomposition import PCA, TruncatedSVD
# New_df is from the random undersample data (fewer instances)
X = under_sample_data.drop('Class', axis=1)
y = under_sample_data['Class']
# PCA Implementation
t0 = time.time()
X_reduced_pca = PCA(n_components=2, random_state=42).fit_transform(X.values)
t1 = time.time()
print("PCA took {:.2} s".format(t1 - t0))
# TruncatedSVD
t0 = time.time()
X_reduced_svd = TruncatedSVD(n_components=2, algorithm='randomized', random_state=42).fit_transform(X.values)
t1 = time.time()
print("Truncated SVD took {:.2} s".format(t1 - t0))
import matplotlib.patches as mpatches
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(24,6))
# labels = ['No Fraud', 'Fraud']
f.suptitle('Clusters using Dimensionality Reduction', fontsize=14)
blue_patch = mpatches.Patch(color='#0A0AFF', label='No Fraud')
red_patch = mpatches.Patch(color='#AF0000', label='Fraud')
# PCA scatter plot
ax1.scatter(X_reduced_pca[:,0], X_reduced_pca[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax1.scatter(X_reduced_pca[:,0], X_reduced_pca[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax1.set_title('PCA', fontsize=14)
ax1.grid(True)
ax1.legend(handles=[blue_patch, red_patch])
# TruncatedSVD scatter plot
ax2.scatter(X_reduced_svd[:,0], X_reduced_svd[:,1], c=(y == 0), cmap='coolwarm', label='No Fraud', linewidths=2)
ax2.scatter(X_reduced_svd[:,0], X_reduced_svd[:,1], c=(y == 1), cmap='coolwarm', label='Fraud', linewidths=2)
ax2.set_title('Truncated SVD', fontsize=14)
ax2.grid(True)
ax2.legend(handles=[blue_patch, red_patch])
plt.show()
四、数据建模与评估
4.1 K折交叉验证
使用K折交叉验证,对欠采样样本进行建模分析,以Recall值进行评估
def printing_Kfold_scores(x_train_data,y_train_data):
fold = KFold(5,shuffle=False)
c_param_range = [0.01,0.1,1,10,100]
results_table = pd.DataFrame(index=range(len(c_param_range),2), columns=['C_parameter','Mean recall score'])
results_table['C_parameter'] = c_param_range
j = 0
for c_param in c_param_range:
recall_accs = []
for iteration, indices in enumerate(fold.split(x_train_data),start=1):
lr = LogisticRegression(C=c_param,penalty='l1')
lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
recall_accs.append(recall_acc)
print('Iteration ', iteration,': recall score = ', recall_acc)
results_table.ix[j,'Mean recall score'] = np.mean(recall_accs)
j += 1
print('')
print('Mean recall score ', np.mean(recall_accs))
print('')
best_c = results_table.loc[results_table['Mean recall score'].astype(float).idxmax()]['C_parameter']
return best_c
best_c = printing_Kfold_scores(X_train_undersample,y_train_undersample)
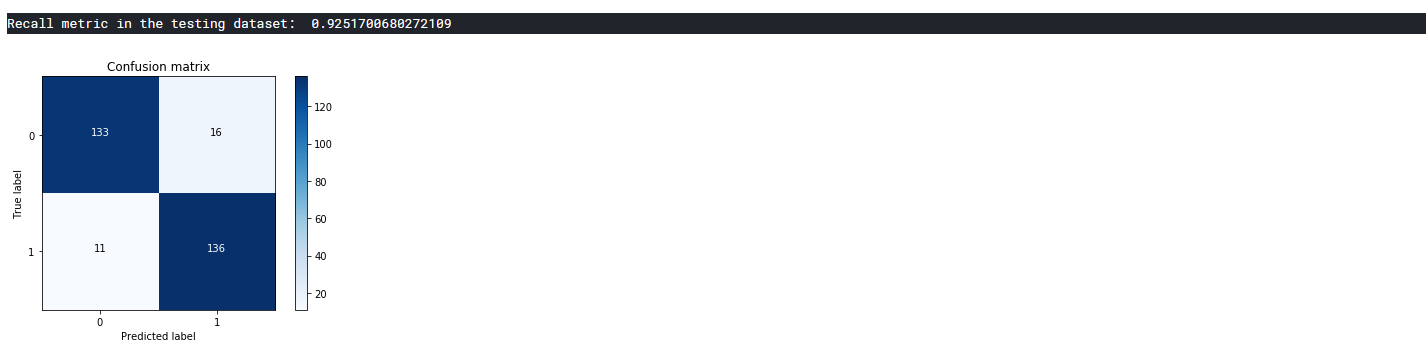
4.2 混淆矩阵
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
import itertools
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample = lr.predict(X_test_undersample.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample,y_pred_undersample)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
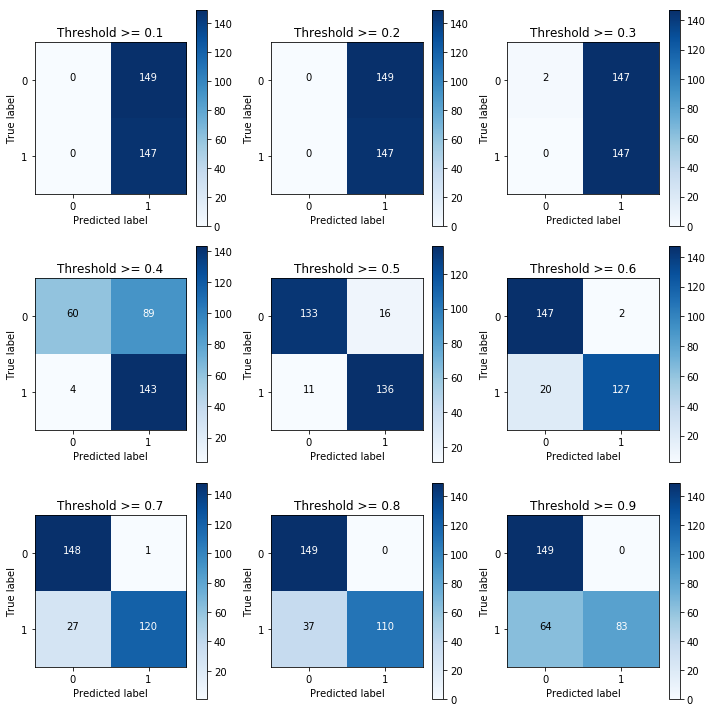
4.3 阀值分析
调节LR模型的threshold,选择最优的阀值。
lr = LogisticRegression(C = 0.01, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
plt.figure(figsize=(10,10))
j = 1
for i in thresholds:
y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > i
plt.subplot(3,3,j)
j += 1
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample,y_test_predictions_high_recall)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Threshold >= %s'%i)
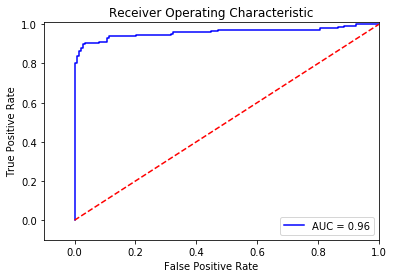
4.4 ROC曲线
分析模型的ROC曲线以及使用此模型对欠采样得到的数据集under_sample进行分析,结果如下。
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred = lr.predict(X_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion matrix')
plt.show()
y_pred_undersample_score = lr.fit(X_train_undersample,y_train_undersample.values.ravel()).decision_function(X_test_undersample.values)
fpr, tpr, thresholds = roc_curve(y_test_undersample.values.ravel(),y_pred_undersample_score)
roc_auc = auc(fpr,tpr)
# Plot ROC
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.1,1.0])
plt.ylim([-0.1,1.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
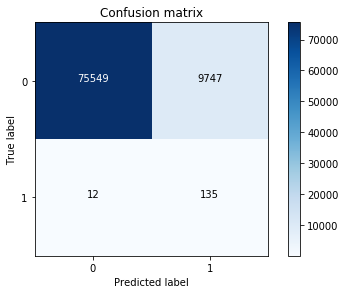
4.4 原始数据分析
由之前的LR模型对原始数据进行预测分析
best_c = printing_Kfold_scores(X_train,y_train)
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train,y_train.values.ravel())
y_pred_undersample = lr.predict(X_test.values)
cnf_matrix = confusion_matrix(y_test,y_pred_undersample)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
lr = LogisticRegression(C = best_c, penalty = 'l1')
y_pred_score = lr.fit(X_train,y_train.values.ravel()).decision_function(X_test.values)
fpr, tpr, thresholds = roc_curve(y_test.values.ravel(),y_pred_score)
roc_auc = auc(fpr,tpr)
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.1,1.0])
plt.ylim([-0.1,1.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()

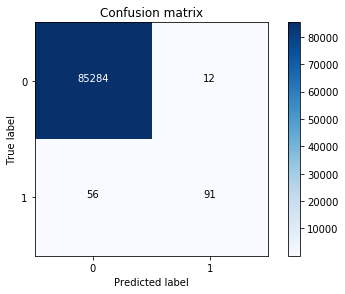
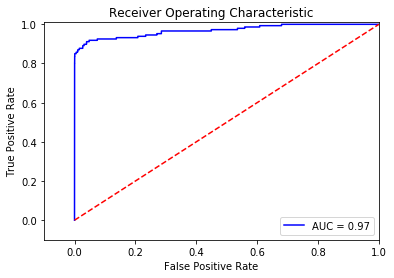
可以看直接使用模型训练并不能获得很好的召回率,也就是说并不能很好的辨别盗刷交易,下面采用前面所说的过采样进行处理。
4.5 过采样处理
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
data = pd.read_csv('../input/creditcard.csv')
from sklearn.preprocessing import StandardScaler
data['normAmount'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1,1))
data = data.drop(['Amount','Time'], axis=1)
import itertools
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report
def printing_Kfold_scores(x_train_data,y_train_data):
fold = KFold(5,shuffle=False)
c_param_range = [0.01,0.1,1,10,100]
results_table = pd.DataFrame(index=range(len(c_param_range),2), columns=['C_parameter','Mean recall score'])
results_table['C_parameter'] = c_param_range
j = 0
for c_param in c_param_range:
recall_accs = []
for iteration, indices in enumerate(fold.split(x_train_data),start=1):
lr = LogisticRegression(C=c_param,penalty='l1')
lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
recall_accs.append(recall_acc)
print('Iteration ', iteration,': recall score = ', recall_acc)
results_table.ix[j,'Mean recall score'] = np.mean(recall_accs)
j += 1
print('')
print('Mean recall score ', np.mean(recall_accs))
print('')
best_c = results_table.loc[results_table['Mean recall score'].astype(float).idxmax()]['C_parameter']
return best_c
def plot_confusion_matrix(cm, classes, title='Confusion matrix', cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
columns=data.columns
features_columns=columns.delete(len(columns)-1)
features=data[features_columns]
labels=data['Class']
features_train, features_test, labels_train, labels_test = train_test_split(features, labels, test_size=0.3, random_state=0)
oversampler=SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_sample(features_train,labels_train)
os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
best_c = printing_Kfold_scores(os_features,os_labels)
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", float(cnf_matrix[1,1])/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, title='Confusion matrix')
plt.show()
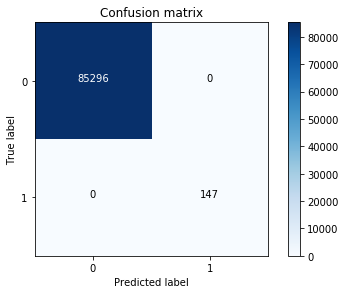
五、结论
- 在遇到数据不平衡时一定要进行处理,若按原数据集进行训练有可能模型无意义,此外数据间差异过大需要进行归一化。
- 通过下采样(Random undersampling) 处理数据得到的逻辑回归模型,虽然recall值挺高的,但NP值非常高,也就是误杀率非常高。此为下采样处理数据的弊端,过采样来处理数据,效果优于下采样
- 逻辑回归模型中除了惩罚力度参数C需要整定,Threshold也可以调,使得模型的各项指标最优
- 特征工程中的降温处理非常有必要,在高维数据集中包含许多不必要的数据时。
- 待完善的地方是需要结合不同的机器学习算法进行数据集训练,如决策树、SVM、随机森林、GBDT、XGBoost等,综合分析最好的模型。此外还可依据模型制定评分卡,通过评分卡对欺诈行为进行预测。