剑指offer[10]——矩形覆盖

题目描述

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

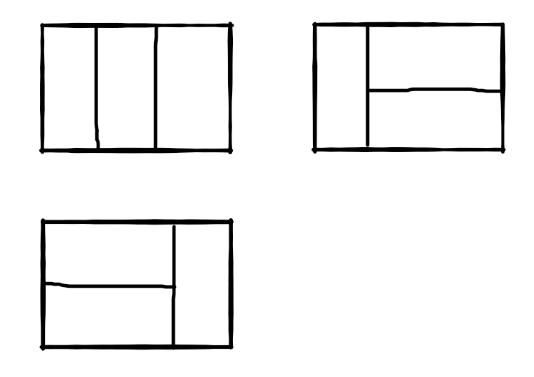
比如n=3时，2*3的矩形块有3种覆盖方法：

这个题目我想到两种思路，一种是斐波那契数列，另一种是排列组合

排列组合

其实仔细观察这道题我们会发现，2*3的矩形块的3种覆盖方法可以写为：

[1+1+1=3 ]

[1+2=3 ]

[2+1=3 ]

仔细观察大家会发现，3可以由m个2与n个1加和而成（其中2*m+n=3），当3全部由1组成的时候只有一种情况，而当3由1和2组成的时候有两种情况，这种情况就是由排列组合算出，公式如下：

[rectCover={A_{m+n}^{m+n}over{A_{m}^{m}*A_{n}^{n}}} ]

在算这道题目的时候大家就是遍历可以有多少个2，而2X3的矩阵最多只能有一个2，下面我们来看一下2X5矩形的情况，可以有0个、1个、2个2，我们就进行依次计算：

[{A_{5}^{5}over{A_{0}^{0}*A_{5}^{5}}}=1 ]

[{A_{4}^{4}over{A_{1}^{1}*A_{3}^{3}}}=4 ]

[{A_{3}^{3}over{A_{2}^{2}*A_{1}^{1}}}=3 ]

所以一共有1+4+3=8种情况，代码如下：

function rectCover(number)
{
    if(number<=0) {return 0;}
    let res = [1];
    let n=1;
    for(let i=1; i<=number; i++){
        n *= i;
        res.push(n);
    }
    let index = 0;
    let sum = 0;
    while((number - 2*index) >= 0){
        sum += res[number-index]/(res[number - 2*index]*res[index]);
        index++;
    }
    return sum;
}

斐波那契数列

这种思路其实和前两道题目大体相似，不太明白的可以去前两道题目看一下，这里只给出代码：

function rectCover(number) {
    if (number <= 2){
        return number;
    }
    let pre1 = 2; // n 最后使用一块，剩下 n-1 块的写法
    let pre2 = 1; // n 最后使用两块，剩下 n-2 块的写法
    for (let i = 3; i <= number; i++){
        let cur = pre1 + pre2;
        pre2 = pre1;
        pre1 = cur;
    }
    return pre1; //相对于 n+1 块来说，第 n 种的方法
}