思路:最小费用最大流
提交:(1)次
题解:
拆点
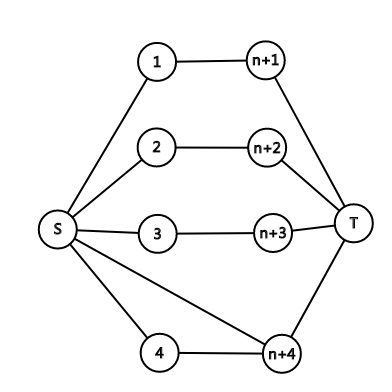
对于题目中的边((u,v))且(u<v),则连((u,v+n)),流量为(1),费用为边权。
对于能力爆发,连边((S,i+n)),流量为(1),费用为能力爆发的代价。
最大流一定会跑满(即边((i+n,T))满流),代表所有点都只经过一遍。
((S,i+n))满流代表使用了能力爆发,
((u,v+n))满流代表选择边((u,v))。
#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
#define ll long long
#define R register int
using namespace std;
namespace Luitaryi {
template<class I> inline I g(I& x) { x=0;
register I f=1; register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*=f;
} const int N=1610,M=20010,Inf=0x3f3f3f3f;
int n,m,s,t,cnt=1,ans; bool vis[N];
int vr[M<<1],nxt[M<<1],w[M<<1],c[M<<1],fir[N],d[N];
inline void add(int u,int v,int ww,int cc) {vr[++cnt]=v,nxt[cnt]=fir[u],w[cnt]=ww,c[cnt]=cc,fir[u]=cnt;}
inline bool spfa() { memset(d,0x3f,sizeof(d)),memset(vis,0,sizeof(vis));
queue<int> q; q.push(s),d[s]=0,vis[s]=true;
while(!q.empty()) { R u=q.front(); q.pop(); vis[u]=false;
for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
if(w[i]&&d[v]>d[u]+c[i]) {
d[v]=d[u]+c[i];
if(!vis[v]) q.push(v),vis[v]=true;
}
}
} return d[t]<Inf;
}
inline int dfs(int u,int f) { vis[u]=true;
if(u==t||f<=0) return f; R res=f;
for(R i=fir[u];i;i=nxt[i]) { R v=vr[i];
if(!vis[v]&&w[i]&&d[v]==d[u]+c[i]) {
R tmp=dfs(v,min(w[i],res));
res-=tmp,w[i]-=tmp,w[i^1]+=tmp;
if(!res) return f;
}
} return f-res;
}
inline void dinic() { R tmp;
while(spfa()) while(tmp=dfs(s,Inf),tmp!=0)
memset(vis,0,sizeof(vis)),ans+=tmp*d[t];
}
inline void main() {
g(n),g(m),s=n*2+1,t=n*2+2;
for(R i=1;i<=n;++i) add(s,i,1,0),add(i,s,0,0),add(n+i,t,1,0),add(t,n+i,0,0);
for(R i=1,x;i<=n;++i) g(x),add(s,n+i,1,x),add(n+i,s,0,-x);
for(R i=1,u,v,w;i<=m;++i) {
g(u),g(v),g(w); u>v?swap(u,v):(void)(0);
add(u,v+n,1,w),add(v+n,u,0,-w);
}
dinic(); printf("%d
",ans);
}
} signed main() {Luitaryi::main(); return 0;}
2019.08.17
83