Luogu P5018 对称二叉树 瞎搞树&哈希

我的天。。普及组这么$hard$。。。

然后好像没有人用我的垃圾做法，，，好像是$O(n)$，但十分的慢，并且极其暴力$qwq$

具体来说，就是直接$dfs$求出树高，然后想像出把原来的树补成满二叉树的形态

$likespace this:$

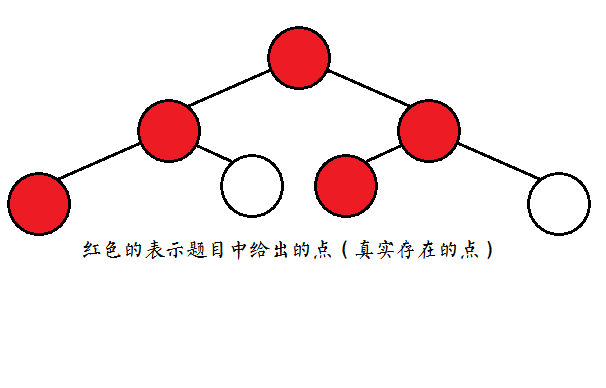
震不震惊$qwq$

然后对子树哈希,同时保存正向的哈希值$h1[u]$和反向的哈希值$h2[u]$（对称时用）。
但每次向上合并时要乘的是$Base^{sz+0/1}$,其中$sz=$子树所形成的完全二叉树的大小。

这样哈希值既可以表示点位置（不同的位置点在完全二叉树中的位置不同），又可以表示点的数值。

如果还不懂可以康康代码

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define R register int
using namespace std;
#define ull unsigned long long
#define ll long long
#define pause (for(R i=1;i<=10000000000;++i))
#define IN freopen("NOIPAK++.in","r",stdin)
#define OUT freopen("out.out","w",stdout)
namespace Fread {
    static char B[1<<15],*S=B,*D=B;
#ifndef JACK
    #define getchar() (S==D&&(D=(S=B)+fread(B,1,1<<15,stdin),S==D)?EOF:*S++)
#endif
    inline int g() {
        R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix;
        if(ch==EOF) return EOF; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix;
    } inline bool isempty(const char& ch) {return (ch<=36||ch>=127);}
    inline void gs(char* s) {
        register char ch; while(isempty(ch=getchar()));
        do *s++=ch; while(!isempty(ch=getchar()));
    }
}using Fread::g; using Fread::gs;
const int N=1000010,B=2333;
int ch[N][2];
#define ls ch[u][0]
#define rs ch[u][1]
int n,w[N],sz[N],d[N],ans,mxd;
ull h1[N],h2[N],p[N],tmp;
inline void dfs1(int u) { mxd=max(d[u],mxd);
    if(~ls) d[ls]=d[u]+1,dfs1(ls); if(~rs) d[rs]=d[u]+1,dfs1(rs);
}
inline void dfs(int u) {sz[u]=1; 
    if(~ls) dfs(ls),sz[u]+=sz[ls]; if(~rs) dfs(rs),sz[u]+=sz[rs];
    if(~ls&&~rs&&sz[ls]==sz[rs]&&h1[ls]==h2[rs]&&h2[ls]==h1[rs]) ans=max(ans,sz[u]);
    if(!~ls&&!~rs) h1[u]=h2[u]=w[u],ans=max(ans,1); else if(~ls&&!~rs) h1[u]=h1[ls]*p[d[u]]+w[u]*(p[d[u]]-1),h2[u]=h2[ls]+w[u]*(p[d[u]]-1);
    else if(!~ls&&~rs) h1[u]=w[u]*(p[d[u]]-1)+h1[rs],h2[u]=w[u]*(p[d[u]]-1)+h2[rs]*p[d[u]];
    else h1[u]=h1[ls]*p[d[u]]+w[u]*(p[d[u]]-1)+h1[rs],h2[u]=h2[ls]+w[u]*(p[d[u]]-1)+h2[rs]*p[d[u]];
}
signed main() {
#ifdef JACK
IN;
#endif
    n=g(); for(R i=1;i<=n;++i) w[i]=g(); for(R u=1;u<=n;++u) ls=g(),rs=g(); 
    d[1]=1; dfs1(1);
    for(R i=1;i<=n;++i) d[i]=mxd-d[i]; p[0]=1; tmp=p[1]=B; for(R i=1;i<=mxd;++i) p[i+1]=(tmp*=tmp);
    dfs(1); printf("%d
",ans);
}

---

2019.07.08/09