今天翻了翻其他大佬的博客,发现自己有些。。。颓废。。。
有必要洗心革面,好好学习
序:正常的BST有可能退化,成为链,大大降低效率,所以有很多方法来保持左右size的平衡,本文将简单介绍Treap,Splay,替罪羊,FHQ Treap;
另:代码都是普通平衡树
1.Treap
树堆,在数据结构中也称Treap,是指有一个随机附加域满足堆的性质的二叉搜索树,其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树,Treap的特点是实现简单,且能基本实现随机平衡的结构。——百度百科
好的treap=tree+heap(为何不叫hee??)
首先易知堆是棵二叉树,BST也是棵二叉树,
又易知:当堆的中的数据是随机插入(即不是有序数据&&有序插入),堆的的高度是趋于log级别的
于是我们让BST中的节点满足堆性质,让BST中的每一个节点带上一个随机权值dat,作为他在这个满足堆性质的BST中的优先级;
然后为了让BST中的节点满足堆性质,我们要rotate(旋)他
易知以下两种是等价的
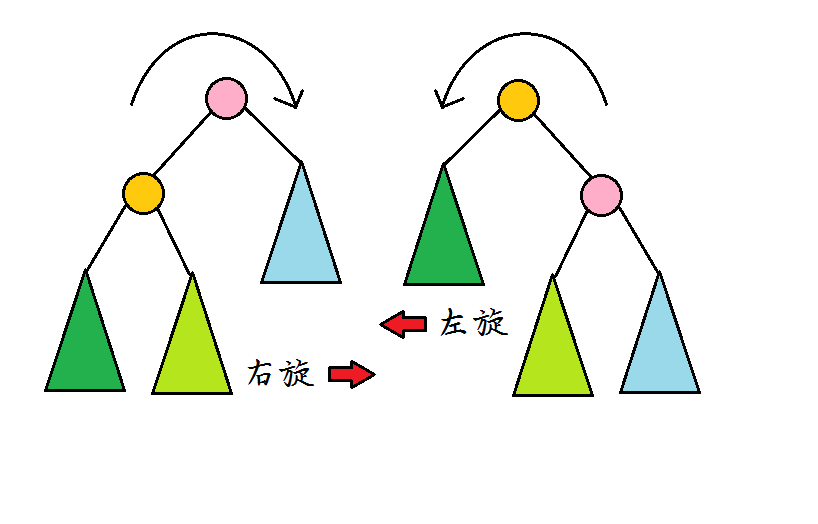
仍然满足BST的性质,但是改变了父子关系。
这就是如何在BST中维护堆性质:旋,改变父子关系,直到满足堆性质
PS:此处的旋好像叫单旋,只会改变父子关系,而Splay有一种操作较双旋(见下)
rotate(旋)在一类BST中我认为是最重要的操作
上代码:
ch[x][0/1]左右儿子,vl[x]权值,dat[x]在堆中的优先级,sz[x]子树大小,cnt[x]是vl[x]出现的次数
#include<cstdio> #include<iostream> #include<cstdlib> #define ls ch[x][0] #define rs ch[x][1] #define R register int using namespace std; const int N=100010,Inf=0x3f3f3f3f; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } int n,tot,rt; int sz[N],ch[N][2],vl[N],dat[N],cnt[N]; inline void upd(int x) {sz[x]=sz[ls]+sz[rs]+cnt[x];} inline int cre(int v) {R x=++tot; cnt[x]=1,vl[x]=v,dat[x]=rand(),upd(x); return tot;} inline void rot(int& x,int d) { R y=ch[x][d]; ch[x][d]=ch[y][d^1]; ch[y][d^1]=x; upd(x),upd(y); x=y; } inline void ins(int& x,int v) { if(!x) {x=cre(v); return ;} if(vl[x]==v) {++cnt[x]; upd(x); return ;} R d=vl[x]<v; ins(ch[x][d],v); upd(x); if(dat[ch[x][d]]<dat[x]) rot(x,d); } inline void del(int& x,int v) { if(!x) return ; if(vl[x]==v) { if(cnt[x]>1) --cnt[x]; else { if(!ls) x=rs; else if(!rs) x=ls; else {R d=dat[ls]>dat[rs]; rot(x,d); del(ch[x][d^1],v);}//看谁大就把谁旋上来,把根旋下去 } } else del(ch[x][vl[x]<v],v); upd(x); } inline void build() {srand(100023323); rt=cre(-Inf); ins(rt,Inf);} inline int getpre(int x,int v) { if(!x) return -Inf; if(vl[x]<v) return max(getpre(rs,v),vl[x]);//右边可能没有 else return getpre(ls,v); } inline int getnxt(int x,int v) { if(!x) return Inf; if(vl[x]>v) return min(getnxt(ls,v),vl[x]);//同上 else return getnxt(rs,v); } inline int getrk(int x,int v) { if(!x) return 0; if(vl[x]==v) return sz[ls]+1; else if(vl[x]>v) return getrk(ls,v); else return sz[ls]+cnt[x]+getrk(rs,v); } inline int getvl(int x,int rk) { if(!x||!rk) return 0; if(rk<=sz[ls]) return getvl(ls,rk); else if(rk<=sz[ls]+cnt[x]) return x; return getvl(rs,rk-sz[ls]-cnt[x]); } signed main() { //freopen("in.in","r",stdin);freopen("out.out","w",stdout); n=g(); for(R i=1;i<=n;++i) { R k=g(),x=g(); if(k==1) ins(rt,x); else if(k==2) del(rt,x); else if(k==3) printf("%d ",getrk(rt,x)); else if(k==4) printf("%d ",vl[getvl(rt,x)]); else if(k==5) printf("%d ",getpre(rt,x)); else printf("%d ",getnxt(rt,x)); } //while(1); }
2.Splay
伸展树(Splay)是一种平衡二叉树,即优化后的二叉查找树。伸展树可以自我调整,这就要依靠伸展操作Splay(x,S),使得提升效率。——洛谷日报
Splay,伸展树。。。维持左右子树平衡用到了另一种旋:双旋
设fa[x]=y,fa[y]=g
双旋,同时改变x,y与y,g之间的关系,它会使g变成x的孙子,y变为x的孩子,g变为y的孩子
分两种情况:
第一种如下
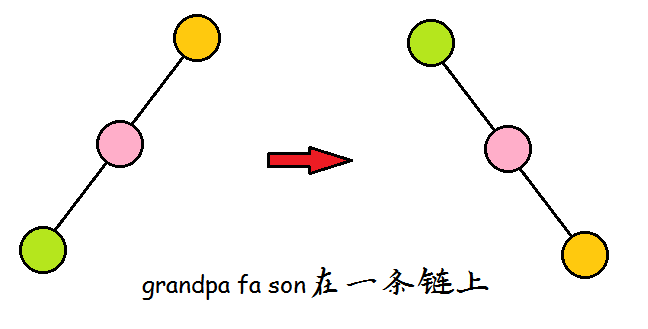
此时要先旋fa,再旋son(纯手绘不喜勿喷qwq);
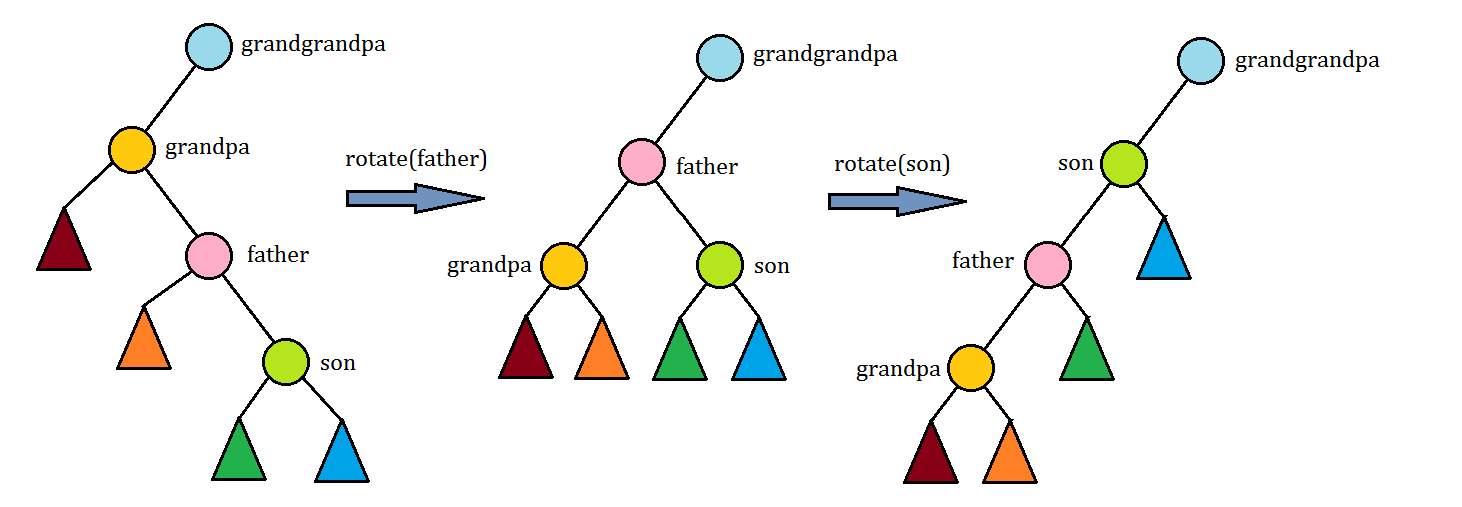
第二种如下(不在一条链)
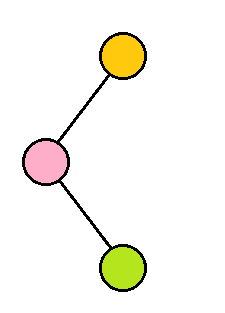
那么我们旋两次son

然后Splay的思路是:不管如何操作,将操作的点通过两种旋法,旋至根节点
至于为什么这么旋请找tarjan。。。至于时间复杂度请找tarjan
#include<cstdio> #include<iostream> #define R register int #define ls (ch[x][0]) #define rs (ch[x][1]) const int N=100005,Inf=0x3f3f3f3f; using namespace std; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } int n,tot; int fa[N],ch[N][2],sz[N],vl[N],cnt[N]; inline int cre(int v) {vl[++tot]=v,sz[tot]=cnt[tot]=1; return tot;} inline void upd(int x) {sz[x]=sz[ls]+cnt[x]+sz[rs];} inline void rot(int x) { R y=fa[x],d=ch[y][1]==x; if(fa[y]) ch[fa[y]][ch[fa[y]][1]==y]=x; fa[x]=fa[y]; fa[ch[y][d]=ch[x][d^1]]=y; fa[ch[x][d^1]=y]=x; upd(y); } int rt; inline void print(int x) { if(!x) return ; print(ls); printf("%d ",vl[x]); print(rs); } inline void Splay(int x,int f) { while(fa[x]!=f) { R y=fa[x]; if(fa[y]!=f) rot((ch[y][1]==x)==(ch[fa[y]][1]==y)?y:x); //在不在一条链上 rot(x); } upd(x); if(!f) rt=x; } inline void ins(int v) { R x=rt; while(1) { if(vl[x]==v) {++cnt[x]; break;} if(!ch[x][vl[x]<v]) { fa[ch[x][vl[x]<v]=cre(v)]=x; x=tot; break; } x=ch[x][vl[x]<v]; } Splay(x,0); } inline void build() {rt=cre(Inf),ins(-Inf);} inline int getrk(int v) { R x=rt,ret=0; while(1) { if(vl[x]==v) {ret+=sz[ls]+1; Splay(x,0); return ret;} if(vl[x]<v) ret+=sz[ls]+cnt[x]; if(!ch[x][vl[x]<v]) {++ret; Splay(x,0); return ret;} x=ch[x][vl[x]<v]; } } inline int getpos(int x,int k) { if(!x) return 0; if(k<=sz[ls]) return getpos(ls,k); if(k<=sz[ls]+cnt[x]) return x; return getpos(rs,k-sz[ls]-cnt[x]); } inline int getvl(int rk) {R x=getpos(rt,rk); Splay(x,0); return vl[x];} inline int getmx(int x,int y) {if(!x||!y) return x|y; return vl[x]>vl[y]?x:y;} inline int ppos(int x,int v) { if(!x) return 0; if(vl[x]<v) return getmx(x,ppos(rs,v)); return ppos(ls,v); } inline int getpre(int v) {R x=ppos(rt,v); Splay(x,0); return vl[x];} inline int getmn(int x,int y) {if(!x||!y) return x|y; return vl[x]<vl[y]?x:y;} inline int npos(int x,int v) { if(!x) return 0; if(v<vl[x]) return getmn(x,npos(ls,v)); return npos(rs,v); } inline int getnxt(int v) {R x=npos(rt,v); Splay(x,0); return vl[x];} inline void del(int v) { Splay(ppos(rt,v),0),Splay(npos(rt,v),rt); R& x=ch[ch[rt][1]][0]; if(!(--cnt[x])) x=0; else Splay(x,0); } signed main() { //freopen("in.in","r",stdin); R n=g(); build(); while(n--) { R k=g(),x=g(); if(k==1) ins(x); else if(k==2) del(x); else if(k==3) printf("%d ",getrk(x)-1); else if(k==4) printf("%d ",getvl(x+1)); else if(k==5) printf("%d ",getpre(x)); else printf("%d ",getnxt(x)); } //system("pause"); while(1); }
3.替罪羊树
为何叫替罪羊。。。据说拍扁他是他儿子的锅。。。
替罪羊维护左右孩子平衡思路:当max(size(x.ls),size(x.rs))>size(x)*alpha(一个常量,一般0.7-0.8,看个人的喜好。。。),就暴力重构以x为根的子树。
具体地,就是把树拍扁,扔到数组中sort一遍,然后选mid,递归左子树和右子树;
然而替罪羊的删除是懒惰删除。。就是打一个tag。、所以用到儿子时要向下传递。。暴力重构时把删除的节点扔到内存池里去
所以, 特别地,当整个树实际存在的的节点数<整个树的节点数*B(另一个常量,合法范围是0.0-1.0,至于取多少看个人)
变量:sum总节点数=实际存在的节点数+删除的节点数; sz实际存在的节点数;del删除标记;mem存储删除的或没有使用的点;tmp存储拍扁重构的的点
#include<cstdio> #include<iostream> #define R register int using namespace std; const double A=0.72,RB=0.53; const int N=100010; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } struct node{ int ls,rs,vl,sz,sum,del; #define ls(x) t[x].ls #define rs(x) t[x].rs #define vl(x) t[x].vl #define sz(x) t[x].sz #define sum(x) t[x].sum #define del(x) t[x].del }t[N]; int n,rt; int mem[N],cm,tmp[N],ct; inline bool ck(int x) {return (double)sz(x)*A<=(double)max(sz(ls(x)),sz(rs(x)));} inline void dfs(int x) { if(!x) return ; dfs(ls(x)); if(!del(x)) tmp[++ct]=x; else mem[++cm]=x; dfs(rs(x)); } inline void build(int& x,int l,int r) { R md=l+r>>1; x=tmp[md]; if(l==r) { ls(x)=rs(x)=del(x)=0; sz(x)=sum(x)=1; return ; } if(l<md) build(ls(x),l,md-1); else ls(x)=0; build(rs(x),md+1,r); sz(x)=sz(ls(x))+sz(rs(x))+1, sum(x)=sum(ls(x))+sum(rs(x))+1; } inline void rebuild(int& x) { ct=0; dfs(x); if(ct) build(x,1,ct); else x=0; } inline void ins(int& x,int vl) { if(!x) { x=mem[cm--]; vl(x)=vl,ls(x)=rs(x)=del(x)=0; sz(x)=sum(x)=1; return ; } ++sz(x),++sum(x); if(vl(x)>=vl) ins(ls(x),vl); else ins(rs(x),vl); if(ck(x)) rebuild(x); } inline int getrk(int vl) { R x=rt; R ret=1; while(x) { if(vl(x)>=vl) x=ls(x); else {ret+=sz(ls(x))+(del(x)==0); x=rs(x);} } return ret; } inline int getvl(int rk) { R x=rt; while(x) { //cout<<x<<" "<<vl(x)<<endl; if(del(x)==0&&sz(ls(x))+1==rk) return vl(x); else { if(sz(ls(x))+1>rk) x=ls(x); else { rk-=sz(ls(x))+(del(x)==0); x=rs(x); } } } } inline void delrk(int& x,int rk) { if(del(x)==0&&sz(ls(x))+1==rk) {del(x)=1; --sz(x); return ;} --sz(x); if(sz(ls(x))+(del(x)==0)>=rk) delrk(ls(x),rk); else delrk(rs(x),rk-sz(ls(x))-(del(x)==0)); } inline void delvl(int vl) { R x=getrk(vl); //cerr<<x<<endl; delrk(rt,x); if(sum(rt)*RB>=sz(rt)) rebuild(rt); } signed main() { //freopen("in.in","r",stdin); freopen("out.out","w",stdout); n=g(); for(R i=100000;i>=1;--i) mem[++cm]=i; while(n--) { R k=g(),x=g(); if(k==1) ins(rt,x); else if(k==2) delvl(x); else if(k==3) printf("%d ",getrk(x)); else if(k==4) printf("%d ",getvl(x)); else if(k==5) printf("%d ",getvl(getrk(x)-1)); else if(k==6) printf("%d ",getvl(getrk(x+1))); } //while(1); }
4.FHQ Treap
首先%%%fhq%%%
其次就是这个Treap不用旋,很好理解。。。
两个操作:split和merge
1.split(int o,int v,int& x,int& y) 把以o为根的树分<=v和>v的两部分
也可按照rank去分成两部分
2.merge(int x,int y) 合并以x和y为根的子树,返回新的根的值
短小而精悍。。。
#include<cstdio> #include<iostream> #include<cstdlib> #define R register int #define ls(i) ch[i][0] #define rs(i) ch[i][1] using namespace std; const int N=500010; inline int g() { R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix; } int tot; int ch[N][2],sz[N],vl[N],dat[N]; inline void upd(int x) {sz[x]=sz[ls(x)]+sz[rs(x)]+1;} inline int cre(int v) {R x=++tot; sz[x]=1,vl[x]=v,dat[x]=rand();return x;} inline int merge(int x,int y) { if(!x||!y) return x+y; if(dat[x]<dat[y]) {rs(x)=merge(rs(x),y); upd(x); return x;} else {ls(y)=merge(x,ls(y)); upd(y); return y;} } inline void split(int o,int v,int& x,int& y) { if(!o) {x=y=0; return ;} if(vl[o]<=v) x=o,split(rs(o),v,rs(o),y); else y=o,split(ls(o),v,x,ls(o)); upd(o); } inline int getvl(int x,int rk) { while(1) { if(rk<=sz[ls(x)]) x=ls(x); else if(rk==sz[ls(x)]+1) return x; else rk-=sz[ls(x)]+1,x=rs(x); } } signed main() { srand(100023323u); R n,x,y,z,rt=0; //freopen("1.in","r",stdin);freopen("out.out","w",stdout); n=g(); while(n--) { //cerr<<n<<" "<<rt<<" "<<endl; R k=g(),a=g(); if(k==1) split(rt,a,x,y),rt=merge(merge(x,cre(a)),y); else if(k==2) {split(rt,a,x,z),split(x,a-1,x,y); y=merge(ls(y),rs(y)),rt=merge(merge(x,y),z);} else if(k==3) split(rt,a-1,x,y),printf("%d ",sz[x]+1),rt=merge(x,y); else if(k==4) printf("%d ",vl[getvl(rt,a)]); else if(k==5) split(rt,a-1,x,y),printf("%d ",vl[getvl(x,sz[x])]),rt=merge(x,y); else if(k==6) split(rt,a,x,y),printf("%d ",vl[getvl(y,1)]),rt=merge(x,y); } while(1); }
2019.05.05&&2019.05.06