题目描述
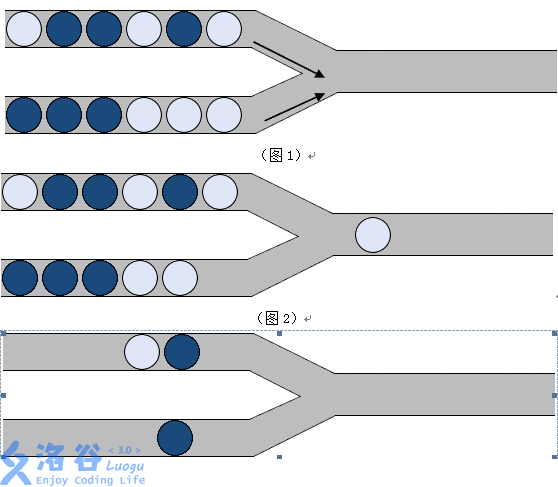
管道取珠是小X很喜欢的一款游戏。在本题中,我们将考虑该游戏的一个简单改版。游戏画面如图1所示:
(图1)
游戏初始时,左侧上下两个管道分别有一定数量的小球(有深色球和浅色球两种类型),而右侧输出管道为空。每一次操作,可以从左侧选择一个管道,并将该管道中最右侧的球推入右边输出管道。
例如:我们首先从下管道中移一个球到输出管道中,将得到图2所示的情况。
(图2)
假设上管道中有n个球, 下管道中有m个球,则整个游戏过程需要进行n+m次操作,即将所有左侧管道中的球移入输出管道。最终n+m个球在输出管道中从右到左形成输出序列。
爱好数学的小X知道,他共有C(n+m,n)种不同的操作方式,而不同的操作方式可能导致相同的输出序列。举个例子,对于图3所示的游戏情形:
(图3)
我们用A表示浅色球,B表示深色球。并设移动上管道右侧球的操作为U,移动下管道右侧球的操作为D,则共有C(2+1,1)=3种不同的操作方式,分别为UUD,UDU,DUU;最终在输出管道中形成的输出序列(从右到左)分别为BAB,BBA,BBA。可以发现后两种操作方式将得到同样的输出序列。
假设最终可能产生的不同种类的输出序列共有K种,其中:第i种输出序列的产生方式(即不同的操作方式数目)有ai个。聪明的小X早已知道,
Σai=C(n+m,n)
因此,小X希望计算得到:
Σ(ai)^2
你能帮助他计算这个值么?由于这个值可能很大,因此只需要输出该值对1024523的取模即可(即除以1024523的余数)。
说明:文中C(n+m,n)表示组合数。组合数C(a,b)等价于在a个不同的物品中选取b个的选取方案数。
输入输出格式
输入格式:
输入文件中的第一行为两个整数n,m,分别表示上下两个管道中球的数目。
第二行中为一个AB字符串,长度为n,表示上管道中从左到右球的类型。其中:A表示浅色球,B表示深色球。
第三行中为一个AB字符串,长度为m,表示下管道中的情形。
输出格式:
输出文件中仅一行为一个整数,即为 除以1024523的余数。
输入输出样例
说明
【样例说明】
样例即为文中(图3)。共有两种不同的输出序列形式,序列BAB有1种产生方式,而序列BBA有2种产生方式,因此答案为5。
【数据规模和约定】
对于30%的数据,满足:m,n<=12;
对于100%的数据,满足:m,n<=500。
一种新的dp姿势qwq,统计∑a[i] ^ 2 就相当于统计有多少 有序方案相同,或者简单的说就是取两次,第二次的序列和第一次的序列一样的方案数,直接暴力四维dp即可,因为最后一维受限,实际上只有三维,转移O(1),可以滚动数组。。。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int ha=1024523,maxn=505;
inline void ADD(int &x,int y){ x+=y; if(x>=ha) x-=ha;}
int f[2][maxn][maxn],n,m,now,nxt;
char A[maxn],B[maxn];
inline void dp(){
f[now=0][m][n]=1,nxt=1;
for(int i=n;i>=0;i--,now=nxt,nxt^=1){
memset(f[nxt],0,sizeof(f[nxt]));
for(int j=m;j>=0;j--)
for(int k=n,o;k>=0;k--) if(f[now][j][k]){
o=i+j-k;
if(i){
if(A[i]==A[k]) ADD(f[nxt][j][k-1],f[now][j][k]);
if(A[i]==B[o]) ADD(f[nxt][j][k],f[now][j][k]);
}
if(j){
if(B[j]==A[k]) ADD(f[now][j-1][k-1],f[now][j][k]);
if(B[j]==B[o]) ADD(f[now][j-1][k],f[now][j][k]);
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
scanf("%s%s",A+1,B+1);
A[0]='~',B[0]='@',dp();
printf("%d
",f[nxt][0][0]);
return 0;
}