【BZOJ3144】【HNOI2013】切糕

总算做了一道2011以后的省选题了……
原题：

图片题面好评！

P,Q,R≤40，0≤D≤R，给出的所有的不和谐值不超过1000。

文本样例好评！

恩这个是听妹主席讲过后会写的，首先把每个点拆成链，那么割掉这个链上的某条边就表示这个点选了某个权值，边的流量就是这个点设成这个值的花费，表示要花费掉这些代价来把这条边割掉

相邻两个点的值之差<=d怎么搞呐，假设两个相邻的点x，y，那么x的第i个点往y的i-d个点连oo的边，即可，大概就像酱紫：

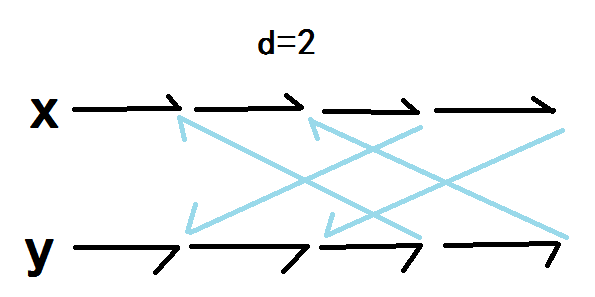
 如果有两个被割掉的线段距离超过d，就依然存在一条路径从s到t，就要继续割

差不多是酱紫：

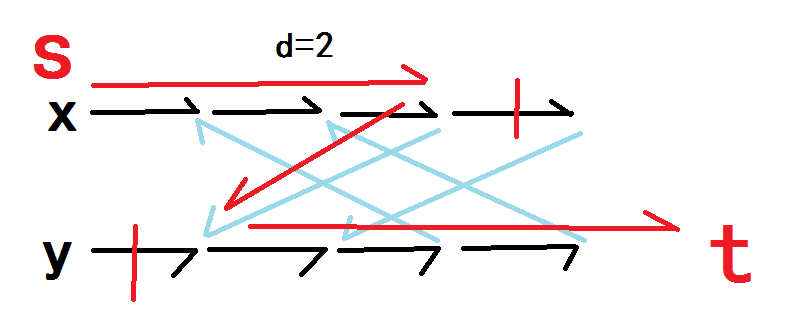
恩就酱

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int oo=168430090;
int rd(){int z=0,mk=1;  char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')mk=-1;  ch=getchar();}
    while(ch>='0'&&ch<='9'){z=(z<<3)+(z<<1)+ch-'0';  ch=getchar();}
    return z*mk;
}
struct ddd{int nxt,y,v,rvs;}e[2100000];  int lk[66100],ltp=0;
inline void ist(int x,int y,int z){
    e[++ltp].nxt=lk[x],lk[x]=ltp,e[ltp].y=y,e[ltp].v=z,e[ltp].rvs=ltp+1;
    e[++ltp].nxt=lk[y],lk[y]=ltp,e[ltp].y=x,e[ltp].v=0,e[ltp].rvs=ltp-1;
}
const int fx[4]={1,-1,0,0},fy[4]={0,0,1,-1};
int n,m,h,d;  int N;  int s,t;
int lvl[66100];
int q[66100],hd=0;
bool gtlvl(){
    memset(lvl,0,sizeof(lvl));
    q[hd=1]=s,lvl[s]=1;
    for(int k=1;k<=hd;++k)
        for(int i=lk[q[k]];i;i=e[i].nxt)if(e[i].v && !lvl[e[i].y])
            lvl[e[i].y]=lvl[q[k]]+1,q[++hd]=e[i].y;
    return lvl[t];
}
int mxflw(int x,int y){
    if(x==t)  return y;
    int bwl=0,flw=0;
    for(int i=lk[x];i && bwl<y;i=e[i].nxt)if(e[i].v && lvl[e[i].y]==lvl[x]+1)
        if((flw=mxflw(e[i].y,min(y-bwl,e[i].v)))){
            bwl+=flw;
            e[i].v-=flw,e[e[i].rvs].v+=flw;
        }
    if(!bwl)  lvl[x]=0;
    return bwl;
}
int dnc(){
    int bwl=0,flw=0;
    while(gtlvl())while((flw=mxflw(s,oo)))  bwl+=flw;
    return bwl;
}
bool chck(int x,int y,int z){
    return x+fx[z]>=1 && x+fx[z]<=n && y+fy[z]>=1 && y+fy[z]<=m;
}
inline int gtid(int x,int y,int z){  return z*N+(x-1)*m+y;}
int main(){//freopen("ddd.in","r",stdin);
    cin>>n>>m>>h>>d;  N=n*m;  s=0,t=N*(h+1)+1;
    for(int k=1;k<=h;++k)for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)
        ist(gtid(i,j,k-1),gtid(i,j,k),rd());
    for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)for(int k=0;k<4;++k)if(chck(i,j,k))
        for(int p=1;p+d<=h;++p){
            ist(gtid(i,j,p+d),gtid(i+fx[k],j+fy[k],p),oo);
            ist(gtid(i+fx[k],j+fy[k],p+d),gtid(i,j,p),oo);
        }
    for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)  ist(s,gtid(i,j,0),oo),ist(gtid(i,j,h),t,oo);
    cout<<dnc()<<endl;
    return 0;
}