感觉相比其他树归题简单多了,不过有点绕(也许是我的思路很奇怪一。一)(这是省选题啊,就算作为T1这题也太水了,HA好弱……)
原题:
对于一棵树,我们可以将某条链和与该链相连的边抽出来,看上去就象成一个毛毛虫,点数越多,毛毛虫就越大。例如下图左边的树(图1)抽出一部分就变成了右边的一个毛毛虫了(图2)。
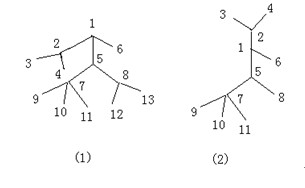
N≤300000
先搞出有根树,这回不枚举中间点了,说说我的奇怪的做法一。一
搞两个数组,一个是uf,表示包括自己在内的直系最大值,另一个是bf,表示x和x往下的兄弟中uf最大的一个
然后就是求uf和bf
uf[x]=bf[tree[x].child]+tree[x].cnum;//不用减uf最大的内个儿子,因为还有自己
如果x是叶子,也就是child[x]==0,uf[x]=1
bf[x]=max(uf[x],bf[tree[x].brother]);
因为根不一定在答案上,所以设一个全局最大值ans,求uf和bf后,ans=max(ans,uf[x]+bf[tree[x].brother]+tree[tree[x].father].cnum-(tree[x].father==1));
这里不用减去两个儿子,因为还有爹和爷,然而当tree[x].father==1(我把根设为1)的时候要-1,因为根没有爹
最后直接输出ans即可
(用全局最大值来更新答案应该是很多DP的策略)
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 using namespace std; 7 int read(){int z=0,mark=1; char ch=getchar(); 8 while(ch<'0'||ch>'9'){if(ch=='-')mark=-1; ch=getchar();} 9 while(ch>='0'&&ch<='9'){z=(z<<3)+(z<<1)+ch-'0'; ch=getchar();} 10 return z*mark; 11 } 12 struct ddd{int next,y;}e[610000];int LINK[310000],ltop=0; 13 inline void insert(int x,int y){e[++ltop].next=LINK[x];LINK[x]=ltop;e[ltop].y=y;} 14 struct dcd{int brother,child,father, cnum;}tree[310000]; 15 inline void insert_tree(int x,int y){tree[y].brother=tree[x].child;tree[x].child=y;tree[y].father=x; tree[x].cnum++;} 16 int n,m; 17 int uf[310000],bf[310000];//bf表示众多兄弟中谁最大,uf表示直系最大 18 int ans=0; 19 void get_tree(int x){ 20 for(int i=LINK[x];i;i=e[i].next)if(e[i].y!=tree[x].father){ 21 insert_tree(x,e[i].y); 22 get_tree(e[i].y); 23 } 24 } 25 void dp_tree(int x){ 26 if(!x) return ; 27 dp_tree(tree[x].brother); 28 if(tree[x].child){ 29 dp_tree(tree[x].child); 30 uf[x]=bf[tree[x].child]+tree[x].cnum;//不用减uf最大的内个儿子,因为还有自己 31 } 32 else 33 uf[x]=1; 34 bf[x]=max(uf[x],bf[tree[x].brother]); 35 ans=max(ans,uf[x]+bf[tree[x].brother]+tree[tree[x].father].cnum-(tree[x].father==1));//不用减去两个儿子,因为还有爹和爷 36 } 37 int main(){//freopen("ddd.in","r",stdin); 38 memset(uf,0,sizeof(uf)); 39 memset(bf,0,sizeof(bf)); 40 cin>>n>>m;//其实m就等于n-1吧一。一 41 int _left,_right; 42 for(int i=1;i<=m;i++){ _left=read(),_right=read(); insert(_left,_right),insert(_right,_left);} 43 get_tree(1); 44 dp_tree(1); 45 cout<<ans<<endl; 46 return 0; 47 }
