嗯,先上题目描述。。。
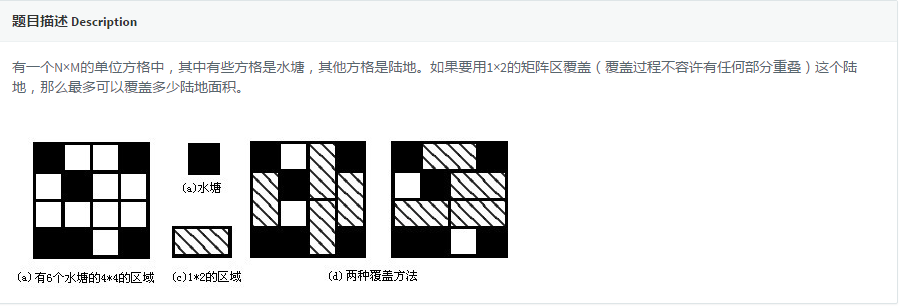



此题接近裸的匈牙利算法,将陆地和其四周是陆地的点连一条边,这样就有了一个无向图。
接着就是从第一个点出发枚举未被标记的点,标记与其对应的另一个点(因为是1*2的长方形)。
开了一个四维数组e[x1][y1][x2][y2],若为零代表点(x1,y1)与(x2,y2)不连通。
match[x1][y1][1]放与点(x1,y1)配对的另一个点的x,match[x1][y1][2]放与点(x1,y1)配对点的y。
还有就是更改的时候记得双向更改,因为是无向图啊。
然后就跑dfs,代码应该是可以看得懂的吧。。。

#include<cstdio> #include<cstring> int m,n,k; int cc[4][2]={{0,1},{0,-1},{1,0},{-1,0}}; int e[102][102][102][102]={0}; bool ok[102][102],book[102][102]; int match[102][102][3]; bool dfs(int x,int y) { for(int i=0;i<4;i++) { int p1=x+cc[i][0]; int p2=y+cc[i][1]; if(p1>=1&&p1<=m&&p2>=1&&p2<=n) { if(!book[p1][p2]&&e[x][y][p1][p2]) { book[p1][p2]=1; if(!match[p1][p2][1]||dfs(match[p1][p2][1],match[p1][p2][2])) { match[p1][p2][1]=x; match[p1][p2][2]=y; match[x][y][1]=p1; match[x][y][2]=p2; return true; } } } } return false; } int main() { memset(ok,true,sizeof(ok)); memset(match,0,sizeof(match)); int sum=0; scanf("%d %d %d",&m,&n,&k); int l,r; for(int i=1;i<=k;i++) { scanf("%d %d",&l,&r); ok[l][r]=false; } for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) { if(ok[i][j]) { if(i+1<=m&&ok[i+1][j]) { e[i][j][i+1][j]=1; e[i+1][j][i][j]=1; } if(j+1<=n&&ok[i][j+1]) { e[i][j][i][j+1]=1; e[i][j+1][i][j]=1; } } } } for(int i=1;i<=m;i++) { for(int j=1;j<=n;j++) { if(!ok[i][j])continue; memset(book,0,sizeof(book)); if(!match[i][j][1]&&dfs(i,j))sum++; } } printf("%d",sum); return 0; }
