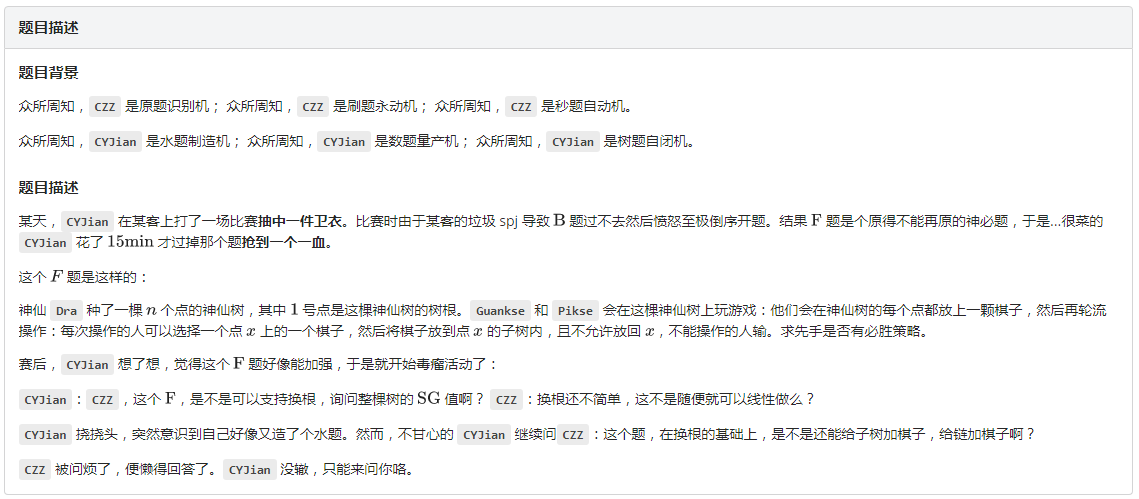
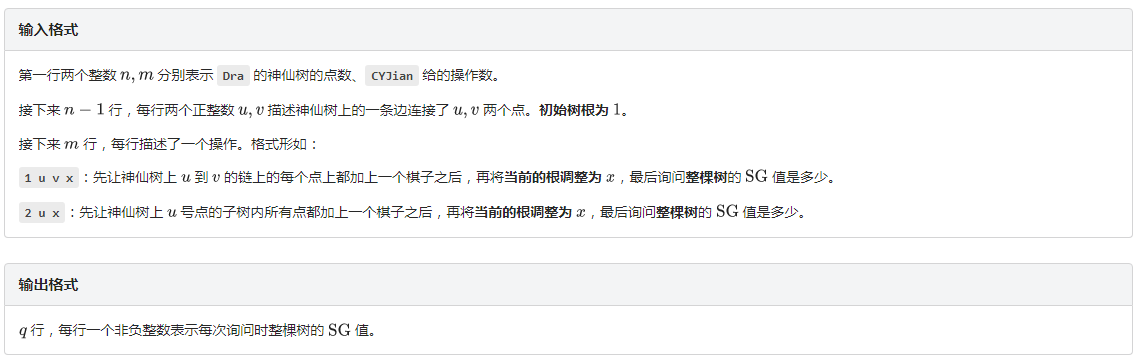
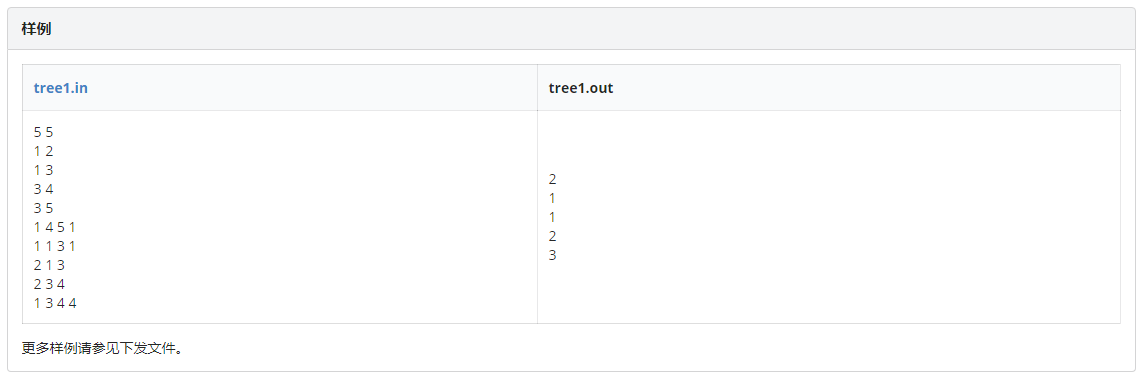
题目描述:

分析:
人傻了,神仙码农题写半天调半天
首先要看出每个点SG函数的规律,就是该点到其子树内最远点的距离
理性分析一下,画图看看发现很有道理(
如果根是确定的,那么SG函数就确定,树链剖分+线段树反转操作维护每个点的石头数的奇偶性计算贡献
换根让题目变难了很多
首先有个结论,对于\(n\)种根,每个点SG函数的取值只会有2种

然后这个\(f\)和\(g\),两次dfs就可以算出来
确定一个点为根,这样有的点SG函数是\(f\),有的是\(g\),搞起来很头疼
如果确定直径的中点为根,那么所有点的SG函数就都是\(g\)了
\(f\)所属的路径必定经过直径中点(奥妙重重)
那么这个时候,我们从直径中点换根为\(x\)时,路径上的点的SG值都会变成\(f\)
只有中点本身需要分类讨论一下(有点恶心)
这个也相当于一个翻转操作,\(f\)和\(g\)互换
那么线段树每个点维护\(2*2\)的矩阵,分行列两种翻转,可以维护
换根对于路径加石头不影响,对子树就会有影响
假设dfs维护出根为直径中点\(Rt\)的树,目前的根为\(rt\),要修改\(x\)在\(rt\)为根下的子树
如果两者在以\(Rt\)为根的dfs序上不相交或者\(rt\)的子树区间包含\(x\),那么直接修改,否则(即\(x\)为\(rt\)祖先)要变换一下:
如图:

我们找到【\(rt\)在\(x\)的方向】\(p\),修改的区间其实是全区间除去\(p\)的子树区间
还有如果\(x\)就是\(rt\),那么修改的是全区间
树链剖分+线段树翻转操作复杂度\(O(nlog^2n)\)
恶心的细节很多
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#include<vector>
#include<string>
#define maxn 500005
#define INF 0x3f3f3f3f
using namespace std;
inline int getint()
{
int num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
int n,m;
int fir[maxn],nxt[maxn],to[maxn],cnt;
int sz[maxn],fa[maxn],dpt[maxn],son[maxn],tp[maxn];
int pos[maxn],Id[maxn],cur;
struct node{
int a[2][2];
int R,C;
inline void revC(){swap(a[0][0],a[0][1]),swap(a[1][0],a[1][1]),C^=1;}
inline void revR(){swap(a[0][0],a[1][0]),swap(a[0][1],a[1][1]),R^=1;}
}t[maxn<<2];
int f[maxn][2],id[maxn],g[maxn];
int Rt,rt;
inline void newnode(int u,int v)
{to[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;}
inline void getf(int u,int lst)
{
for(int i=fir[u];i;i=nxt[i])if(to[i]!=lst)
{
fa[to[i]]=u,getf(to[i],u);
if(f[to[i]][0]+1>f[u][0])f[u][1]=f[u][0],f[u][0]=f[to[i]][0]+1,id[u]=to[i];
else if(f[to[i]][0]+1>f[u][1])f[u][1]=f[to[i]][0]+1;
}
}
inline void getg(int u,int lst)
{
for(int i=fir[u];i;i=nxt[i])if(to[i]!=lst)
g[to[i]]=max(g[u],id[u]==to[i]?f[u][1]:f[u][0])+1,getg(to[i],u);
}
inline void dfs1(int u)
{
sz[u]=1;
for(int i=fir[u];i;i=nxt[i])if(to[i]!=fa[u])
{
fa[to[i]]=u,dpt[to[i]]=dpt[u]+1;
dfs1(to[i]),sz[u]+=sz[to[i]];
if(sz[son[u]]<sz[to[i]])son[u]=to[i];
}
}
inline void dfs2(int u,int ac)
{
tp[u]=ac,pos[u]=++cur,Id[cur]=u;
if(son[u])dfs2(son[u],ac);
for(int i=fir[u];i;i=nxt[i])if(to[i]!=fa[u]&&to[i]!=son[u])dfs2(to[i],to[i]);
}
inline void pushdown(int i)
{
if(t[i].C)t[i<<1].revC(),t[i<<1|1].revC(),t[i].C=0;
if(t[i].R)t[i<<1].revR(),t[i<<1|1].revR(),t[i].R=0;
}
inline void pushup(int i)
{for(int j=0;j<2;j++)for(int k=0;k<2;k++)t[i].a[j][k]=t[i<<1].a[j][k]^t[i<<1|1].a[j][k];}
inline void modify(int i,int l,int r,int p,int x,int y)
{
if(l==r){t[i].a[0][0]=x,t[i].a[1][0]=y,t[i].a[0][1]=t[i].a[1][1]=0;if(t[i].C)t[i].revC(),t[i].C^=1;return;}
pushdown(i);
int mid=(l+r)>>1;
if(p<=mid)modify(i<<1,l,mid,p,x,y);
else modify(i<<1|1,mid+1,r,p,x,y);
pushup(i);
}
inline void updateR(int i,int l,int r,int ql,int qr)
{
if(qr<l||r<ql)return;
if(ql<=l&&r<=qr){t[i].revR();return;}
pushdown(i);int mid=(l+r)>>1;
updateR(i<<1,l,mid,ql,qr),updateR(i<<1|1,mid+1,r,ql,qr);
pushup(i);
}
inline void updateC(int i,int l,int r,int ql,int qr)
{
if(qr<l||r<ql)return;
if(ql<=l&&r<=qr){t[i].revC();return;}
pushdown(i);int mid=(l+r)>>1;
updateC(i<<1,l,mid,ql,qr),updateC(i<<1|1,mid+1,r,ql,qr);
pushup(i);
}
inline void revR(int u,int p)
{
while(tp[u]!=tp[p])updateR(1,1,n,pos[tp[u]],pos[u]),u=fa[tp[u]];
updateR(1,1,n,pos[p],pos[u]);
}
inline void revC(int u,int v)
{
while(tp[u]!=tp[v])
{
if(dpt[tp[u]]<dpt[tp[v]])swap(u,v);
updateC(1,1,n,pos[tp[u]],pos[u]),u=fa[tp[u]];
}
if(dpt[u]>dpt[v])swap(u,v);
updateC(1,1,n,pos[u],pos[v]);
}
inline int getpos(int u,int p)
{while(tp[u]!=tp[p]){u=tp[u];if(fa[u]==p)return u;u=fa[u];}return son[p];}
inline void transroot(int x)
{
if(rt!=Rt)revR(rt,getpos(rt,Rt)),modify(1,1,n,pos[Rt],f[Rt][0],f[Rt][1]);
rt=x;
if(rt!=Rt)
{
int p=getpos(rt,Rt);
revR(rt,p);
if(p==id[Rt])modify(1,1,n,pos[Rt],f[Rt][1],f[Rt][0]);
else modify(1,1,n,pos[Rt],f[Rt][0],f[Rt][1]);
}
}
int main()
{
n=getint(),m=getint();
for(int i=1;i<n;i++)
{
int u=getint(),v=getint();
newnode(u,v),newnode(v,u);
}
getf(1,1),getg(1,1);
for(int i=1;i<=n;i++)
if(g[i]>f[i][0])f[i][1]=f[i][0],f[i][0]=g[i],id[i]=fa[i];
else if(g[i]>f[i][1])f[i][1]=g[i];
for(int i=1;i<=n;i++)
if(f[i][0]+f[i][1]>f[rt][0]+f[rt][1])rt=i;
else if(f[i][0]-f[i][1]<f[rt][0]-f[rt][1])rt=i;
fa[Rt=rt]=0,dfs1(rt),dfs2(rt,rt);
for(int i=1;i<=n;i++)
if(i!=Rt)modify(1,1,n,pos[i],f[i][1],f[i][0]);
else modify(1,1,n,pos[i],f[i][0],f[i][1]);
transroot(1);
while(m--)
{
int op=getint();
if(op==1)revC(getint(),getint());
else
{
int x=getint();
if(x==rt)updateC(1,1,n,1,n);
else if((pos[x]>=pos[rt]&&pos[x]+sz[x]<=pos[rt]+sz[rt])||pos[x]+sz[x]<=pos[rt]||pos[rt]+sz[rt]<=pos[x])updateC(1,1,n,pos[x],pos[x]+sz[x]-1);
else
{
x=getpos(rt,x);
updateC(1,1,n,1,pos[x]-1);
if(pos[x]+sz[x]<=n)updateC(1,1,n,pos[x]+sz[x],n);
}
}
transroot(getint());
printf("%d\n",t[1].a[0][0]);
}
}
