Ultra-Scalable Spectral Clustering and Ensemble Clustering
1.Abstract:
在U-SPEC中，针对稀疏相似子矩阵的构造，提出了一种混合代表选择策略和k -最近邻代表的快速逼近方法。将稀疏相似子矩阵解释为二部图，利用转移割对图进行有效分割，得到聚类结果:
在U-SENC中，多个U-SPEC聚类器被进一步集成到一个集成聚类框架中，在保持高效的同时增强了U-SPEC的鲁棒性。基于多U-SEPC s的集成生成，构造了一种新的目标与基簇之间的二部图，并对其进行有效分割，达到了一致的聚类结果
U-SPEC和U-SENC都具有近乎线性的时间和空间复杂度
2.Inrtoduction
谱聚类算法因其在处理非线性可分数据集方面具有良好的处理能力，然而，传统光谱聚类的一个关键限制是其巨大的时间和空间复杂度;谱聚类的通常包括两个耗时和消耗内存的阶段，即相似矩阵构建和特征分解。构建相似矩阵一般需要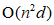
时间和
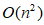内存，求解特征分解问题需要
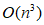时间和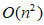
内存，其中N为数据大小，d为维度。随着数据量N的增加，谱聚类的计算量也随之增加。
为了减轻谱聚类的巨大计算负担，常用的策略是：1.稀疏化相似矩阵，用稀疏的特征解算器求解特征分解问题。矩阵稀疏化策略可以降低存储矩阵的内存成本，便于特征分解，但仍然需要计算原相似矩阵中的所有项。2.是基于子矩阵构造：从原始数据集中随机选择p个代表，构建一个n*p相似子矩阵，landmark based spectral clustering(LSC)方法对数据集执行k-means，得到p个聚类中心作为p个代表。然而，这些基于子矩阵的谱聚类方法通常受到复杂度瓶颈(N*p)的限制，这是它们处理超大规模数据集的一个关键障碍，在超大规模数据集中，为了获得更好的近似通常需要更大的p。此外，这些方法的聚类结果严重依赖于子矩阵的一次逼近（逼近实际的n*n矩阵），这对聚类鲁棒性造成了不稳定因素。
本文提出了两种新的大规模算法，即超可伸缩谱聚类(U-SPEC)和超可伸缩集成聚类(U-SENC)。在U-SPEC中，提出了一种新的混合代表选择策略，有效地找到一组p个代表，降低了基于k均值的选择从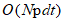
到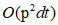
的时间复杂度。 然后，设计了一种 K-nearest 的快速逼近方法，有效地建立了一个具有
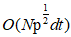时间和
内存的稀疏子矩阵。稀疏的子矩阵作为cross-affinity矩阵,构造bipartite graph之间的数据集和代表集。通过两部图结构transfer cut解决矩阵分解计算量过大的问题, 最后，采用k均值离散化方法构造了一组k个特征向量的聚类结果，该方法耗时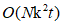
。集成：此外，为了超越U-SPEC的一次性逼近，提供更好的聚类鲁棒性，提出了U-SENC算法，将多个U-SPEC聚类器集成到一个统一的集成聚类框架中，该框架的时间和空间复杂度主要由
和
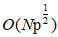控制。
即：
新的混合代表选择策略：找出p个代表
K-nearest 的快速逼近方法：建立了一个np稀疏子矩阵
bipartite graph 的 transfer cut：将np子矩阵解释为二部图，并对其进行有效分割，得到最终的聚类结果
3.PROPOSED FRAMEWORK
3.1新的混合代表选择策略：
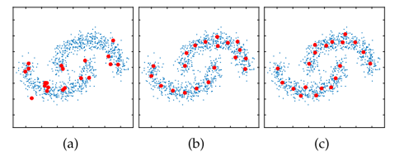
FIG1:图a红点为随机选择的代表点，图b为k_means质心选择出来的代表点，图c为混合方法结果
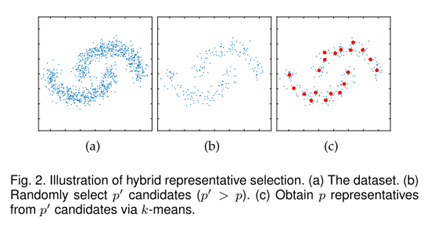
随机的代表选择虽然计算效率高，但固有的随机性可能导致一组低质量的代表；而k_means耗时；而混合方法是先从总数据集中随机抽出一部分数据，再在抽出的部分数据中用k_means学出p个质心作为代表.如图2。
3.2 Approximation of K-Nearest Representatives
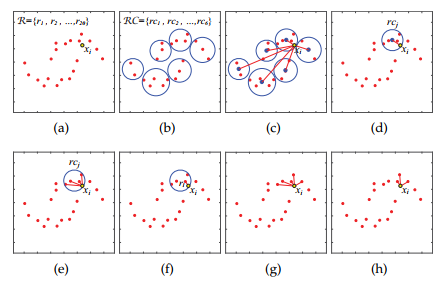
得到p个代表后，下一个目标是通过p个代表对整个数据集的两两关系进行编码，
以往方法子矩阵表示中，对象与代表之间的Np相似子矩阵需要O(Npd)时间和O(Np)内存；后来提出用K-Nearest稀疏np相似度矩阵(每个对象只与其k个最近的代表相连接)，然而，这仍然需要计算N个对象到p个代表之间的所有距离。此外，除了计算Np项总数外，稀疏化步骤还消耗O(NpK)时间；(Ps:注意传统的knn与K-Nearest 有共同特征，但在实际应用中面临不同问题；在子矩阵构造问题中传统knn不适用，因为结构的不平衡p远远小于N.)
为了打破效率瓶颈，这里的关键问题是如何在用K-Nearest的代表构建子矩阵时，显著减少这些中间项的计算.我们提出了一种基于由粗到细机制的K-Nearest表示逼近方法，并用该方法建立了稀疏亲和子矩阵
:我们的k -最近邻代表近似的主要思想是先找到最近邻的区域（将p个代表点聚类，计算样本和P个聚类中心的距离 选出最近的簇），然后在最近邻的区域内找到最近的代表(定义为
)（在最近的代表簇中计算出最近的点），最后在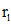
的邻域内找到k -最近邻代表（在最近的点附近k个值作为选中的点）。
3.3 Bipartite Graph Partitioning
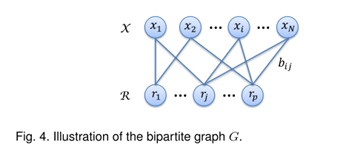
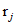：第j个代表
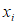：第i个样本
这部分待续