原题链接
将每个城市拆成四个点,即四个机场来看,那么这题就是求最短路。
不过建图有些麻烦,先要找出第四个机场的坐标。
设另外三个机场的坐标为((x_1, y_1), (x_2, y_2), (x_3, y_3)),其中((x_1, y_1), (x_3, y_3))为对角线两点。
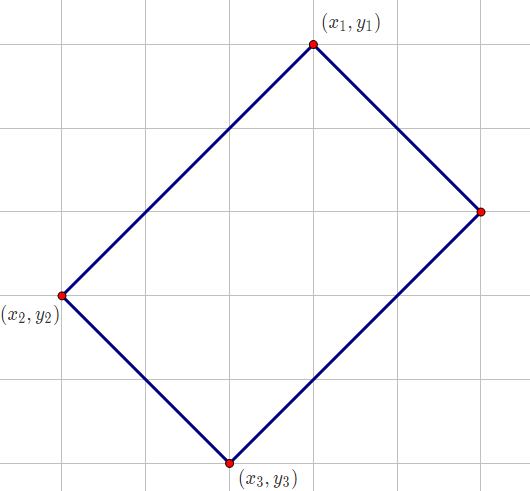
那么第四个点的坐标即为((x_1 + x_3 - x_2, y_1 + y_3 - y_2))。
这个是通过对角线交点为中点,坐标为线段两端点坐标和的一半算得。当然可以用勾股等方法算。
至于找出对角线的两端点,则可以计算原本三点两两之间的长度,那么最长的就是对角线了。当然用勾股也可以判。
然后就之间跑最短路即可。
这里我用的是(dijkstra)。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
const int N = 110;
const int M = 410;
const int K = M * M;
struct dd {
int x;
double D;
bool operator < (const dd &b) const { return D > b.D; }
};
struct poi {
int x[5], y[5], po[5], z;
};
poi a[N];
int fi[M], ne[K], di[K], st, ed, m, l;
double dis[M], da[K];
bool v[M];
priority_queue<dd>q;
inline int re()
{
int x = 0;
char c = getchar();
bool p = 0;
for (; c < '0' || c > '9'; c = getchar())
p |= c == '-';
for (; c >= '0' && c <= '9'; c = getchar())
x = x * 10 + c - '0';
return p ? -x : x;
}
inline double minn(double x, double y) { return x < y ? x : y; }
inline void add(int x, int y, double z)
{
di[++l] = y; da[l] = z; ne[l] = fi[x]; fi[x] = l;
di[++l] = x; da[l] = z; ne[l] = fi[y]; fi[y] = l;
}
inline double calc(int x, int y, int xx, int yy, int z) { return sqrt(1.0 * (x - xx) * (x - xx) + 1.0 * (y - yy) * (y - yy)) * z; }//计算边的花费
inline int fin(int k)//找对角线,顺便添入部分铁路
{
int i, j, L = 0, id;
double D[4], ma = 0;
for (i = 1; i < 3; i++)
for (j = i + 1; j < 4; j++)
{
D[++L] = calc(a[k].x[i], a[k].y[i], a[k].x[j], a[k].y[j], a[k].z);
add(a[k].po[i], a[k].po[j], D[L]);
if (ma < D[L])
ma = D[L], id = L;
}
return id ^ 1 ? id ^ 2 ? 1 : 2 : 3;
}
inline void addp(int x, int y)//将两两城市之间的航道建好
{
for (int i = 1; i < 5; i++)
for (int j = 1; j < 5; j++)
add(a[x].po[i], a[y].po[j], calc(a[x].x[i], a[x].y[i], a[y].x[j], a[y].y[j], m));
}
double dij()//dijkstra
{
int i, x, y;
memset(dis, 66, sizeof(dis));
memset(v, 0, sizeof(v));
for (i = 1; i <= 4; i++)//因为可以从这个城市的任意一个机场出发,所以全部丢进去。
q.push({ a[st].po[i], 0.0 }), dis[a[st].po[i]] = 0;//不知道为什么如果我前面加上结构体类型,VS就不能编译,用C++11的特性才行
while (!q.empty())
{
x = q.top().x;
q.pop();
if (v[x])
continue;
v[x] = 1;
for (i = fi[x]; i; i = ne[i])
if (dis[y = di[i]] > dis[x] + da[i])
{
dis[y] = dis[x] + da[i];
q.push({ y, dis[y] });
}
}
double mi = 1e9;
for (i = 1; i < 5; i++)
mi = minn(mi, dis[a[ed].po[i]]);//取min
return mi;
}
int main()
{
int i, j, t, n, p;
t = re();
while (t--)
{
memset(fi, 0, sizeof(fi));
n = re(); m = re(); st = re(); ed = re();
l = p = 0;
for (i = 1; i <= n; i++)
{
for (j = 1; j < 4; j++)
a[i].x[j] = re(), a[i].y[j] = re(), a[i].po[j] = ++p;
a[i].z = re();
int k = fin(i);
a[i].x[4] = a[i].x[1] + a[i].x[2] + a[i].x[3] - (a[i].x[k] << 1);//计算第四个点的坐标
a[i].y[4] = a[i].y[1] + a[i].y[2] + a[i].y[3] - (a[i].y[k] << 1);
a[i].po[4] = ++p;
for (j = 1; j < 4; j++)
add(a[i].po[4], a[i].po[j], calc(a[i].x[4], a[i].y[4], a[i].x[j], a[i].y[j], a[i].z));
}
for (i = 1; i < n; i++)
for (j = i + 1; j <= n; j++)
addp(i, j);
printf("%.1f
", dij());
}
return 0;
}