前言:寒假讲过了二分图,但没有学会。现在趁着图论复习再学一遍。
------------------
定义:通俗点来讲,如果给你一张图,能将其分为两个点集且点集内部没有连边,那么此图为二分图。
关于二分图有一个性质:二分图一定不存在奇环。证明过程如下:

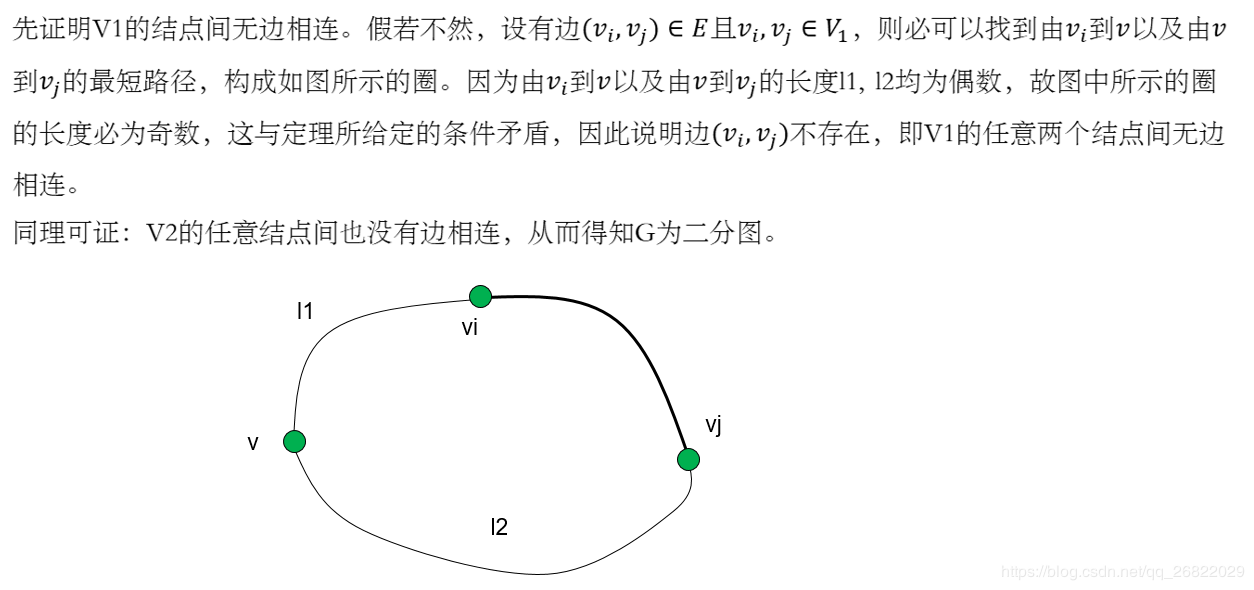
二分图的判定:我们采用染色法。
bfs图,假设把1个点标记成1,那么与它相邻的点都标记成0。如果相邻的点已经被标记过,那么看颜色是否相同。如果相同那么返回$false$。
注意图可能不是联通的,所以我们要$n$个点都找一遍。
bool check(int x) { queue<int> q; q.push(x);color[now]=1; while(!q.empty()) { int now=q.front();q.pop(); for (int i=head[now];i;i=edge[i].next) { int to=edge[i].to; if (color[to]==-1) color[to]=1^color[now]; else if (color[to]==color[now]) return false; } } return true; } memset(color,-1,sizeof(color)); for (int i=1;i<=n;i++) if (color[i]==-1) flag=check(i);
另一种写法,利用搜索树:
bool dfs(int now) { for (int i=0;i<v[now].size();i++) { int to=v[now][i]; if (!dep[to]) dep[to]=dep[now]+1; else{ if ((dep[to]-dep[now])%2==0) return false; } } return true; }
匹配:给定一个二分图G,在G的一个子图M中,M的边集{E}中的任意两条边都不依附于同一个顶点,则称M是一个匹配。
极大匹配(Maximal Matching)是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。
如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
求二分图的最大匹配可以用网络流或匈牙利算法。这里主要讲匈牙利算法的实现。
匈牙利算法核心是找增广路。增广路:若P是图G中一条连通两个未匹配顶点的路径,并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现,则称P为相对于M的一条增广路径。
总体来说步骤有三步:
1.后来的和先来的发生冲突,先来的退让。
2.如果先来的没地方没有其他匹配点,那么后来的寻找其他点。
如果后来的没有匹配点,返回$false$。
$dfs$实现:
bool dfs(int x) { for (int y=1;y<=m;y++) { if (flag[x][y]&&!vis[y]) { vis[y]=1; if (cy[y]==-1||dfs(cy[y])) { cx[x]=y; cy[y]=x; return true; } } } return false; }
洛谷P3386 【模板】二分图最大匹配
代码:
#include<bits/stdc++.h> #define int long long using namespace std; int cx[505],cy[505]; int vis[1005]; bool flag[505][505]; int n,m,e,ans; inline int read() { int x=0,f=1;char ch=getchar(); while(!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x*f; } bool dfs(int x) { for (int y=1;y<=m;y++) { if (flag[x][y]&&!vis[y]) { vis[y]=1; if (cy[y]==-1||dfs(cy[y])) { cx[x]=y; cy[y]=x; return true; } } } return false; } signed main() { n=read(),m=read(),e=read(); for (int i=1;i<=e;i++) { int x=read(),y=read(); if (x>=1&&y>=1&&x<=n&&y<=m) flag[x][y]=true; } memset(cx,-1,sizeof(cx)); memset(cy,-1,sizeof(cy)); for (int i=1;i<=n;i++) { memset(vis,0,sizeof(vis)); ans+=dfs(i); } printf("%d",ans); return 0; }
定理:二分图的最小点覆盖等于二分图最大匹配。二分图最大边覆盖等于$n$减最大匹配。
二分图的最大独立集=顶点数-二分图最大匹配数=二分图最小边覆盖。
-----------------
后记:想要更详细的学习二分图可以去看这个,写得比较详细。毕竟我还是个蒟蒻QAQ。