题目内容:
给定一个长n高2的网格图,如下图:

有三种操作:
1、删除一条边
2、将一条删除的边再加回来
3、询问从一个点到另一个点的不同路径数(不可经过重复边)
算法复杂度要求不能大于 n log n
(由于只有题面,没有输入格式和数据,所以在此只讲一下思路)
正解是用线段树维护。
先给网格图标上号:
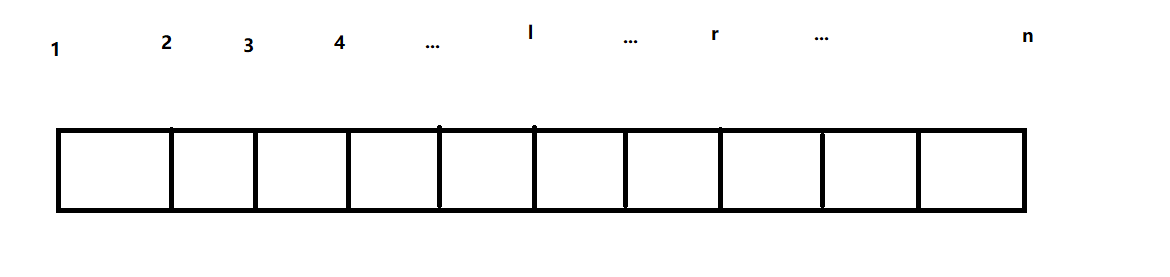
对于线段树上的节点,若它维护的区间为[l,r],则它就对应一个l~r的网格图G: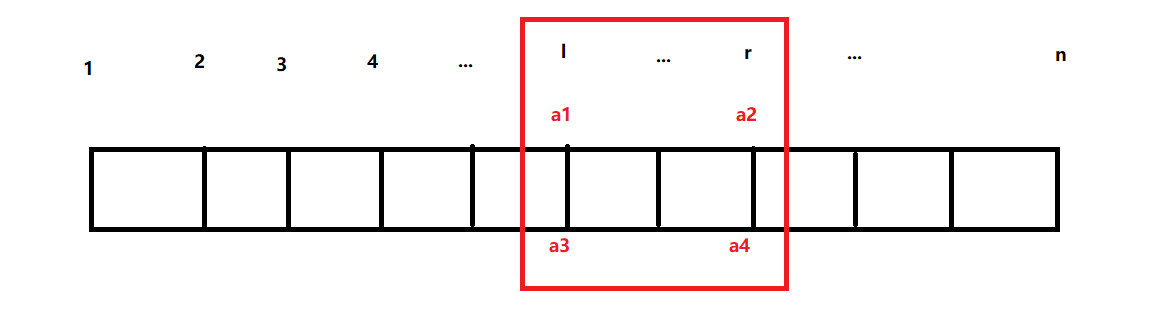
a1、a2、a3、a4分别代表G的左上、右上、左下、右下方的点。同时有布尔变量b1~b6 ,bi表示ai连向外面图部分边的有(1)无(0)(i<=4),b5表示a1-a3这条边的有无,b6表示a2-a4这条边的有无。
有6变量c1~c6,表示在图G中:
c1:从a1到a2的不同路径数
c2:从a1到a4的不同路径数
c3:从a3到a2的不同路径数
c4:从a3到a4的不同路径数
c5:从a1到a3的不同路径数
c6:从a2到a4的不同路径数
c7:是否有一条只走上部分边的路径可由a1到达a2
c8:是否有一条只走上部分边的路径可由a3到达a4

当G的大小为1*2时,此时a1a2重合,a3a4重合,各个变量的值很容易得出,故线段树的叶子结点有初始值。
考虑线段树合并区间向上求的操作:
假设要将区间[l,mid](左)[mid+1,r](右)合并成[l,r](新),对节点的变量一次考虑:
1、对于b:
显然,新b1=左b1,新b2=左b2,新b3=右b3,新b4=右b4,新b5=左b5,新b6=右b6
2、对于c,要仔细考虑一下:

为了便于叙述,将新G的几条关键边的位置记为e1~e4。
对于新c7,新c8,一眼就能看出来怎么维护,故不多说。
对于新c1,路径的形式要么为左a1——左a4——e3——右a3——右a4,得新c1=左c1*右c4*左b4;
要么为左a1——左a2——e1——右a1——右a4,得新c1=左c2*右c1*左b2。
故新c1=左c2*右c1*左b2+左c1*右c4*左b4。
对于c2~c4,可同理分析。
对于c5,有两种情况:
一是路径的所有边都在左图,那么新c5=左c5;
二是有路径的边出现在右图,那么此时一定会经过e1和e3,又因为要保证路径的边不重复,所以有新c5=左c7*左b2*右c5*左b4*左c8
所以新c5=左c7*左b2*右c5*左b4*左c8+左c5
对于c6,可同理分析。
接下来再考虑如何得到答案。
对于询问的两个点u,v,可以先得到他们对应的区间[l,r]

首先想到的就是在线段树中找到[l,r]的答案。但这是不全的,因为线段树中得到的区间[l,r]的答案中的所有路径都是在图[l,r]内部的,但答案还有路径“出图的情况”,如下图:

其实这个也很好办,因为整个图的高只有2,所以"出图”无非只有两种情况:从左边出(即为上图),从右边出。
以从左边出为例:
显然要满足[l,r]对应的b1和b3都等于1,即要有能出图的一对边,这时很容易就想到答案为[1,l-1]的c6*b2*b4。
从右边出同理。
最后这道题就解出来了。其实只要能弄明白线段树的维护信息,这道题就迎刃而解。这些维护信息,多半是由需求而生的。其实说实话,在写这篇题解时,有很多变量也是我在需求下想到的。