
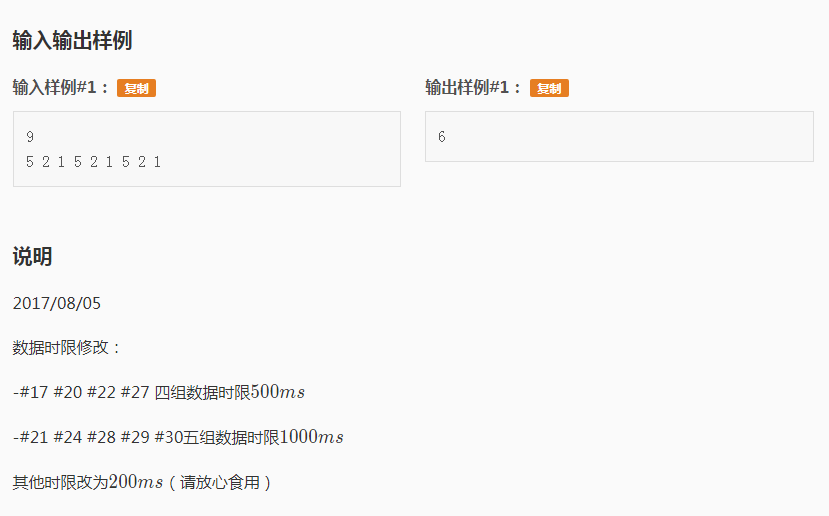
一道特别毒瘤能提醒人不要忘记剪枝的题。
首先不要忘了管理员的话。忘把长度大于50的木棍过滤掉真的坑了不少人(包括我)。
显然是一道DFS题 。考虑剪枝。
找找搜索要面临的维度、状态:原始木棍的长度len,原始木棍的条数m,当前正在拼第k条原始木棍、还剩下没拼完的长度rest,木根的编号。
去等效冗杂考虑:
1、为了祛除冗杂,我们可以假设拼成一根原始木棍的若干小木棍的长度x1,x2,x3,x4,x5...满足x1<x2<x3<x4<x5<...同时把小木棍的长度从大到小排个序,每次找符合条件的小木棍时都从上一个符合条件的小木棍的后面去找,这样就不会有拼成小木棍长度的序列的元素相同,只因为顺序不同就重复搜索的情况了。
2、注意可能有长度相同的小木棍,当我们试完一个小木棍后,再试长度跟它相同的小木棍时,显然得到的情况是一样的,所以应该试下一个长度不同的小木棍,即跳过长度与它相同的小木棍(这里我用预处理处理出每个小木棍的长度与它相等的最后一根小木棍的编号)。
可行性剪枝考虑:
1、一个非常暴力的思路是从0开始到所有木根长度的总和sum枚举len搜索。显然超时妥妥的,所以考虑优化。发现m一定是个整数,所以len一定是sum的因数。而len只需枚举到sum/2就可以了。因为如果len枚举到sum/2后都没找到答案,那答案只能是所有小木棍拼成一个大木棍的长度。
2、当k==m时,剩下的小木棍的长度总和等于len,即一定能拼成一条原始木棍,所以直接回溯即可。
3、当resti(当前找到的小木棍为i时的rest)正好等于找到的符合条件的小木棍i的长度、并把它拼上,之后却不能把所有原始木棍拼出,那么resti在接下来拼木棍时肯定不能得到答案,所以直接回溯。因为resti拼完时,要么使用小木棍i,要么用几根长度和等于小木棍i的长度的小木棍才能刚好把resti拼完。本来那几根小木棍就不能与剩下的小木棍拼出还要拼的原始木棍,当那几根小木棍换成总长度一样,但个数为1的小木棍i后,不就更不能拼出还要拼的原始木棍了吗?
最优性剪枝考虑:找到答案后立即回溯,其他的操作都不管。
实现优化:
1、当我们在找接下来要用哪条木棍拼时可以用二分查找在第last(一条符合条件的小木棍的编号)+1条到最后一条木棍中第一条长度小于等于rest的木棍。
2、我们在每次回溯时把used数组恢复,而避免用memset(memset用多了,慢到崩溃)
AC代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cctype> 6 7 using namespace std; 8 9 bool used[66],bj; 10 11 int a[67],n,sum,m,len,nxt[67],ans; 12 13 char ch; 14 15 bool cmp(int a,int b) 16 { 17 return a>b; 18 } 19 20 inline int read()//吓得都用快读了 21 { 22 ans=0; 23 ch=getchar(); 24 while(!isdigit(ch)) ch=getchar(); 25 while(isdigit(ch)) ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); 26 return ans; 27 } 28 29 void dps(const int &k,const int &last,const int &rest) 30 { 31 if(k==m) {bj=1;return;}//可行性剪枝2 32 if(!rest) 33 { 34 for(int i=1;i<=n;i++) 35 if(!used[i]) 36 { 37 used[i]=1; 38 dps(k+1,i,len-a[i]); 39 used[i]=0;//别忘了回溯,因为可能影响到搜索树的“舅舅节点”。 40 return; 41 } 42 } 43 int l=last+1,r=n,mid; 44 while(l<r)// 45 { 46 mid=(l+r)>>1; 47 if(a[mid]<=rest) r=mid; 48 else l=mid+1; 49 } 50 for(int i=l;i<=n;i++) 51 if(!used[i]) 52 { 53 used[i]=1; 54 dps(k,i,rest-a[i]);//可行性剪枝3 55 if(bj) return;//最优性剪枝 56 used[i]=0; 57 if(rest==a[i]) return; 58 i=nxt[i]; 59 } 60 } 61 62 int main() 63 { 64 n=read(); 65 int tot=0; 66 int b; 67 for(int i=1;i<=n;i++) 68 { 69 b=read(); 70 if(b<=50) 71 { 72 a[++tot]=b; 73 sum+=b; 74 } 75 } 76 n=tot; 77 sort(a+1,a+n+1,cmp); 78 for(int i=n;i>=1;i--)//预处理 79 { 80 if(a[i]==a[i+1]) nxt[i]=nxt[i+1]; 81 else nxt[i]=i; 82 } 83 int s=sum/2;used[1]=1; 84 for(len=a[1];len<=s;len++) 85 if(sum%len==0)//可行性剪枝1 86 { 87 bj=0; 88 m=sum/len; 89 dps(1,1,len-a[1]); 90 if(bj) 91 { 92 printf("%d",len); 93 return 0; 94 } 95 } 96 if(!bj) cout<<sum; 97 return 0; 98 }