Description
小春现在很清闲,面对书桌上的N张牌,他决定给每张染色,目前小春只有3种颜色:红色,蓝色,绿色.他询问Sun有
多少种染色方案,Sun很快就给出了答案.进一步,小春要求染出Sr张红色,Sb张蓝色,Sg张绝色.他又询问有多少种方
案,Sun想了一下,又给出了正确答案. 最后小春发明了M种不同的洗牌法,这里他又问Sun有多少种不同的染色方案.
两种染色方法相同当且仅当其中一种可以通过任意的洗牌法(即可以使用多种洗牌法,而每种方法可以使用多次)洗
成另一种.Sun发现这个问题有点难度,决定交给你,答案可能很大,只要求出答案除以P的余数(P为质数).
Input
第一行输入 5 个整数:Sr,Sb,Sg,m,p(m<=60,m+1<p<100)。n=Sr+Sb+Sg。
接下来 m 行,每行描述一种洗牌法,每行有 n 个用空格隔开的整数 X1X2...Xn,恰为 1 到 n 的一个排列,
表示使用这种洗牌法,第 i位变为原来的 Xi位的牌。输入数据保证任意多次洗牌都可用这 m种洗牌法中的一种代
替,且对每种洗牌法,都存在一种洗牌法使得能回到原状态。
Output
不同染法除以P的余数
Sample Input
1 1 1 2 7
2 3 1
3 1 2
2 3 1
3 1 2
Sample Output
2
HINT
有2 种本质上不同的染色法RGB 和RBG,使用洗牌法231 一次可得GBR 和BGR,使用洗牌法312 一次 可得BRG
和GRB。
100%数据满足 Max{Sr,Sb,Sg}<=20。
Source
这里转载一篇讲的比较好的文章:Burnside引理和Polya定理
引理和定理的区别:
引理是数学中为了取得某个更好的定理而作为步骤被证明的命题,其意义并不在于自身被证明,而在于为达成最终定理作出贡献.
一个引理可用于证明多个定理.数学中存在很多著名的引理,这些引理可能对很多问题的解决有帮助.例如欧几里得引理等
burnside引理:
设G={a1,a2,…ag}是目标集[1,n]上的置换群。每个置换都写成不相交循环的乘积。  是在置换ak的作用下不动点的个数,也就是长度为1的循环的个数。通过上述置换的变换操作后可以相等的元素属于同一个等价类。若G将[1,n]划分成l个等价类,则:等价类个数为:
是在置换ak的作用下不动点的个数,也就是长度为1的循环的个数。通过上述置换的变换操作后可以相等的元素属于同一个等价类。若G将[1,n]划分成l个等价类,则:等价类个数为:
百科上写的什么鬼。。。(黑人问号???)
用这个例子来说明:
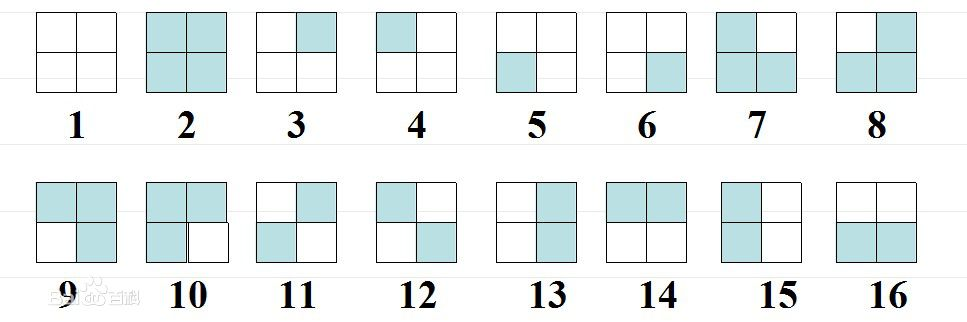
例1:一正方形分成4格,2着色,有多少种方案?其中,经过转动相同的图象算同一方案。
对图中图像的置换可以分为以下四种:
不动:a1=(1)(2)…(16)
逆时针转90度 :a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)
顺时针转90度 :a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)
转180度:a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)
由Burnside引理,共有(16+2+2+4)/4=6(种方案)
这里除以4代表4种方案数
16+2+2+4分别代表每种方案置换后和原本一样的格子
a1:(1)(2)…(16)
a2:(1)(2)
a3:(1)(2)
a4:(1)(2)(11)(12)
然后我们可以写出DP转移方程求方案数:
f[i][j][k]=f[i-d[h]][j][k]+f[i][j-d[h]][k]+f[i][j][k-d[h]]
f[i][j][k]表示r,g,b分别为i,j,k时的方法数
最后使用扩展欧几里德定理求ans%p
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 6 int sr,sb,sg,n,m,p,ans; 7 int a[70][70],f[70][70][70],d[70]; 8 bool b[70]; 9 10 int dp(int x) 11 { 12 memset(b,0,sizeof(b)); 13 int sum=0,t; 14 for(int i=1;i<=n;i++) 15 if(!b[i]) 16 { 17 d[++sum]=1;t=i; 18 b[t]=1; 19 while(!b[a[x][t]]) 20 { 21 d[sum]++; 22 b[a[x][t]]=1; 23 t=a[x][t]; 24 } 25 } 26 memset(f,0,sizeof(f)); 27 f[0][0][0]=1; 28 for(int h=1;h<=sum;h++) 29 for(int i=sr;i>=0;i--) 30 for(int j=sb;j>=0;j--) 31 for(int k=sg;k>=0;k--) 32 { 33 if(i>=d[h]) f[i][j][k]=(f[i][j][k]+f[i-d[h]][j][k])%p; 34 if(j>=d[h]) f[i][j][k]=(f[i][j][k]+f[i][j-d[h]][k])%p; 35 if(k>=d[h]) f[i][j][k]=(f[i][j][k]+f[i][j][k-d[h]])%p; 36 } 37 return f[sr][sb][sg]; 38 } 39 40 int exgcd(int a,int b,int &x,int &y) 41 { 42 if(b==0) 43 { 44 x=1;y=0; 45 return a; 46 } 47 int q=exgcd(b,a%b,y,x); 48 y-=a/b*x; 49 return q; 50 } 51 52 int main() 53 { 54 scanf("%d %d %d %d %d",&sr,&sb,&sg,&m,&p); 55 n=sr+sb+sg; 56 for(int i=1;i<=m;i++) 57 for(int j=1;j<=n;j++) 58 scanf("%d",&a[i][j]); 59 m++; 60 for(int i=1;i<=n;i++) a[m][i]=i; 61 for(int i=1;i<=m;i++) 62 ans=(ans+dp(i))%p; 63 int x,y; 64 exgcd(m,p,x,y); 65 while(x<=0) x+=p,y-=m; 66 printf("%d",ans*x%p); 67 return 0; 68 }