预备知识:
路径:从树中一个结点到另一个结点之间的通路,路径上的分支数目成为路径长度;
树的路径长度:从树根到每一个叶子之间的路径长度之和;
结点的带权路径长度:从该结点到树根之间的路径长度与该结点权值的乘积;
树的带权路径长度:所有叶子结点的带权路径长度之和;
结构相同的任意两颗二叉树,由于他们的叶子结点权值可能不同,所以他们的带权路径长度也会不同;哈夫曼树是指带权路径长度最小的二叉树;
构造哈夫曼树的方法:
假设有一组权值{5,29,7,8,14,23,3,11},下面我们将利用这组权值演示构造哈夫曼树的过程。
第一步:以这8个权值座位根节点的权值构造具有8棵树的森林;

第二步:从中选择两个根的权值最小的树3,5座位左右子树构成一棵新树,新树根节点的权值为3+5,并将这两棵树从森林中删除,并将新树添加进去;

第三步:重复第二步过程,直到森林中只有一棵树为止,此处选择7,8;

第四步:

第五步:

第六步:

第七步:

哈夫曼编码:
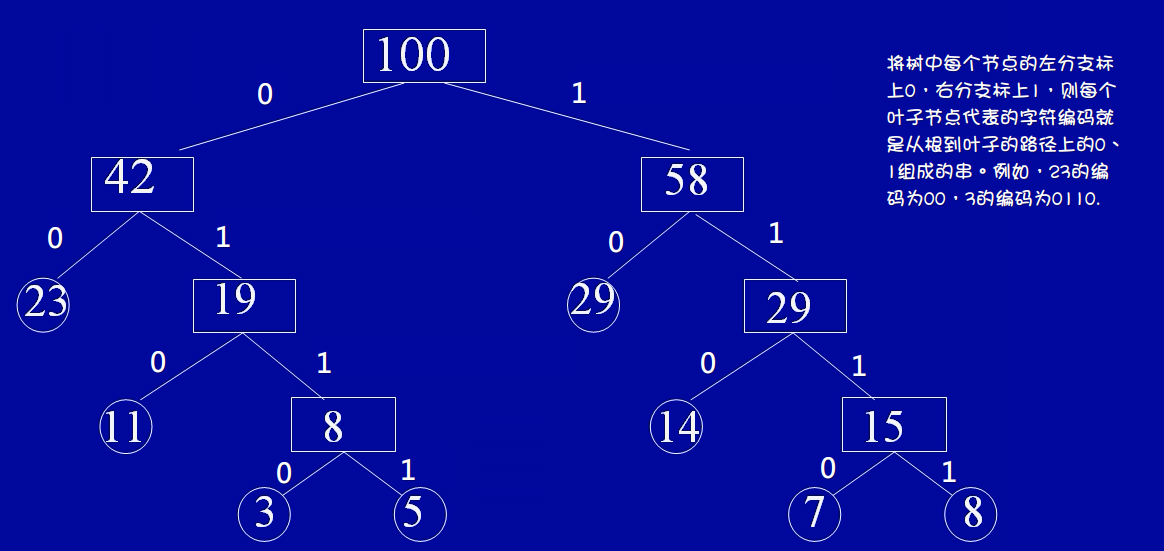
哈夫曼树中只存在叶子节点和度为2的结点。叶子节点的个数=度为2的节点数+1。