模型：
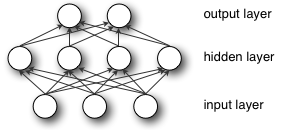
隐含层激活函数常用的有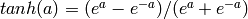
或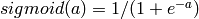
，由于tanh收敛更快，本文采用tanh函数激活函数。
输出采用逻辑回归G
从逻辑回归到MLP
class HiddenLayer(object): def __init__(self, rng, input, n_in, n_out, activation=T.tanh): """ Typical hidden layer of a MLP: units are fully-connected and have sigmoidal activation function. Weight matrix W is of shape (n_in,n_out) and the bias vector b is of shape (n_out,). NOTE : The nonlinearity used here is tanh Hidden unit activation is given by: tanh(dot(input,W) + b) :type rng: numpy.random.RandomState :param rng: a random number generator used to initialize weights :type input: theano.tensor.dmatrix :param input: a symbolic tensor of shape (n_examples, n_in) :type n_in: int :param n_in: dimensionality of input :type n_out: int :param n_out: number of hidden units :type activation: theano.Op or function :param activation: Non linearity to be applied in the hidden layer """ self.input = input
初始化过程：
# `W` is initialized with `W_values` which is uniformely sampled # from sqrt(-6./(n_in+n_hidden)) and sqrt(6./(n_in+n_hidden)) # for tanh activation function # the output of uniform is converted using asarray to dtype # theano.config.floatX so that the code is runable on GPU # Note : optimal initialization of weights is dependent on the # activation function used (among other things). # For example, results presented in [Xavier10]_ suggest that you # should use 4 times larger initial weights for sigmoid # compared to tanh # We have no info for other function, so we use the same as tanh. W_values = numpy.asarray(rng.uniform( low=-numpy.sqrt(6. / (n_in + n_out)), high=numpy.sqrt(6. / (n_in + n_out)), size=(n_in, n_out)), dtype=theano.config.floatX) if activation == theano.tensor.nnet.sigmoid: W_values *= 4 self.W = theano.shared(value=W_values, name='W') b_values = numpy.zeros((n_out,), dtype=theano.config.floatX) self.b = theano.shared(value=b_values, name='b')
所以一个MLP的简单实现如下：
class MLP(object): """Multi-Layer Perceptron Class A multilayer perceptron is a feedforward artificial neural network model that has one layer or more of hidden units and nonlinear activations. Intermediate layers usually have as activation function tanh or the sigmoid function (defined here by a ``HiddenLayer`` class) while the top layer is a softamx layer (defined here by a ``LogisticRegression`` class). """ def __init__(self, rng, input, n_in, n_hidden, n_out): """Initialize the parameters for the multilayer perceptron :type rng: numpy.random.RandomState :param rng: a random number generator used to initialize weights :type input: theano.tensor.TensorType :param input: symbolic variable that describes the input of the architecture (one minibatch) :type n_in: int :param n_in: number of input units, the dimension of the space in which the datapoints lie :type n_hidden: int :param n_hidden: number of hidden units :type n_out: int :param n_out: number of output units, the dimension of the space in which the labels lie """ # Since we are dealing with a one hidden layer MLP, this will # translate into a Hidden Layer connected to the LogisticRegression # layer self.hiddenLayer = HiddenLayer(rng = rng, input = input, n_in = n_in, n_out = n_hidden, activation = T.tanh) # The logistic regression layer gets as input the hidden units # of the hidden layer self.logRegressionLayer = LogisticRegression( input=self.hiddenLayer.output, n_in=n_hidden, n_out=n_out)
同样采用L正则化：
# L1 norm ; one regularization option is to enforce L1 norm to # be small self.L1 = abs(self.hiddenLayer.W).sum() + abs(self.logRegressionLayer.W).sum() # square of L2 norm ; one regularization option is to enforce # square of L2 norm to be small self.L2_sqr = (self.hiddenLayer.W ** 2).sum() + (self.logRegressionLayer.W ** 2).sum() # negative log likelihood of the MLP is given by the negative # log likelihood of the output of the model, computed in the # logistic regression layer self.negative_log_likelihood = self.logRegressionLayer.negative_log_likelihood # same holds for the function computing the number of errors self.errors = self.logRegressionLayer.errors # the parameters of the model are the parameters of the two layer it is # made out of self.params = self.hiddenLayer.params + self.logRegressionLayer.params
和之前一样，我们用在mini-batch上面的随机梯度下降算法训练模型。这里的区别在于，我们修改损失函数并包括规范化项。 L1_reg 和 L2_reg 为超参数，用以控制规范化项在整个损失函数中的比重。计算损失的函数如下：
# the cost we minimize during training is the negative log likelihood of # the model plus the regularization terms (L1 and L2); cost is expressed # here symbolically cost = classifier.negative_log_likelihood(y) + L1_reg * L1 + L2_reg * L2_sqr
接下来，模型参数通过梯度更新。这段代码和之前的基本上一样，除了参数多少的差别。
# compute the gradient of cost with respect to theta (stored in params) # the resulting gradients will be stored in a list gparams gparams = [] for param in classifier.params: gparam = T.grad(cost, param) gparams.append(gparam) # specify how to update the parameters of the model as a list of # (variable, update expression) pairs updates = [] # given two list the zip A = [a1, a2, a3, a4] and B = [b1, b2, b3, b4] of # same length, zip generates a list C of same size, where each element # is a pair formed from the two lists : # C = [(a1, b1), (a2, b2), (a3, b3) , (a4, b4)] for param, gparam in zip(classifier.params, gparams): updates.append((param, param - learning_rate * gparam)) # compiling a Theano function `train_model` that returns the cost, butx # in the same time updates the parameter of the model based on the rules # defined in `updates` train_model = theano.function(inputs=[index], outputs=cost, updates=updates, givens={ x: train_set_x[index * batch_size:(index + 1) * batch_size], y: train_set_y[index * batch_size:(index + 1) * batch_size]})
综合所有代码
""" This tutorial introduces the multilayer perceptron using Theano. A multilayer perceptron is a logistic regressor where instead of feeding the input to the logistic regression you insert a intermediate layer, called the hidden layer, that has a nonlinear activation function (usually tanh or sigmoid) . One can use many such hidden layers making the architecture deep. The tutorial will also tackle the problem of MNIST digit classification. .. math:: f(x) = G( b^{(2)} + W^{(2)}( s( b^{(1)} + W^{(1)} x))), References: - textbooks: "Pattern Recognition and Machine Learning" - Christopher M. Bishop, section 5 """ __docformat__ = 'restructedtext en' import cPickle import gzip import os import sys import time import numpy import theano import theano.tensor as T from logistic_sgd import LogisticRegression, load_data class HiddenLayer(object): def __init__(self, rng, input, n_in, n_out, W=None, b=None, activation=T.tanh): """ Typical hidden layer of a MLP: units are fully-connected and have sigmoidal activation function. Weight matrix W is of shape (n_in,n_out) and the bias vector b is of shape (n_out,). NOTE : The nonlinearity used here is tanh Hidden unit activation is given by: tanh(dot(input,W) + b) :type rng: numpy.random.RandomState :param rng: a random number generator used to initialize weights :type input: theano.tensor.dmatrix :param input: a symbolic tensor of shape (n_examples, n_in) :type n_in: int :param n_in: dimensionality of input :type n_out: int :param n_out: number of hidden units :type activation: theano.Op or function :param activation: Non linearity to be applied in the hidden layer """ self.input = input # `W` is initialized with `W_values` which is uniformely sampled # from sqrt(-6./(n_in+n_hidden)) and sqrt(6./(n_in+n_hidden)) # for tanh activation function # the output of uniform if converted using asarray to dtype # theano.config.floatX so that the code is runable on GPU # Note : optimal initialization of weights is dependent on the # activation function used (among other things). # For example, results presented in [Xavier10] suggest that you # should use 4 times larger initial weights for sigmoid # compared to tanh # We have no info for other function, so we use the same as # tanh. if W is None: W_values = numpy.asarray(rng.uniform( low=-numpy.sqrt(6. / (n_in + n_out)), high=numpy.sqrt(6. / (n_in + n_out)), size=(n_in, n_out)), dtype=theano.config.floatX) if activation == theano.tensor.nnet.sigmoid: W_values *= 4 W = theano.shared(value=W_values, name='W', borrow=True) if b is None: b_values = numpy.zeros((n_out,), dtype=theano.config.floatX) b = theano.shared(value=b_values, name='b', borrow=True) self.W = W self.b = b lin_output = T.dot(input, self.W) + self.b self.output = (lin_output if activation is None else activation(lin_output)) # parameters of the model self.params = [self.W, self.b] class MLP(object): """Multi-Layer Perceptron Class A multilayer perceptron is a feedforward artificial neural network model that has one layer or more of hidden units and nonlinear activations. Intermediate layers usually have as activation function thanh or the sigmoid function (defined here by a ``SigmoidalLayer`` class) while the top layer is a softamx layer (defined here by a ``LogisticRegression`` class). """ def __init__(self, rng, input, n_in, n_hidden, n_out): """Initialize the parameters for the multilayer perceptron :type rng: numpy.random.RandomState :param rng: a random number generator used to initialize weights :type input: theano.tensor.TensorType :param input: symbolic variable that describes the input of the architecture (one minibatch) :type n_in: int :param n_in: number of input units, the dimension of the space in which the datapoints lie :type n_hidden: int :param n_hidden: number of hidden units :type n_out: int :param n_out: number of output units, the dimension of the space in which the labels lie """ # Since we are dealing with a one hidden layer MLP, this will # translate into a TanhLayer connected to the LogisticRegression # layer; this can be replaced by a SigmoidalLayer, or a layer # implementing any other nonlinearity self.hiddenLayer = HiddenLayer(rng=rng, input=input, n_in=n_in, n_out=n_hidden, activation=T.tanh) # The logistic regression layer gets as input the hidden units # of the hidden layer self.logRegressionLayer = LogisticRegression( input=self.hiddenLayer.output, n_in=n_hidden, n_out=n_out) # L1 norm ; one regularization option is to enforce L1 norm to # be small self.L1 = abs(self.hiddenLayer.W).sum() + abs(self.logRegressionLayer.W).sum() # square of L2 norm ; one regularization option is to enforce # square of L2 norm to be small self.L2_sqr = (self.hiddenLayer.W ** 2).sum() + (self.logRegressionLayer.W ** 2).sum() # negative log likelihood of the MLP is given by the negative # log likelihood of the output of the model, computed in the # logistic regression layer self.negative_log_likelihood = self.logRegressionLayer.negative_log_likelihood # same holds for the function computing the number of errors self.errors = self.logRegressionLayer.errors # the parameters of the model are the parameters of the two layer it is # made out of self.params = self.hiddenLayer.params + self.logRegressionLayer.params def test_mlp(learning_rate=0.01, L1_reg=0.00, L2_reg=0.0001, n_epochs=1000, dataset='../data/mnist.pkl.gz', batch_size=20, n_hidden=500): """ Demonstrate stochastic gradient descent optimization for a multilayer perceptron This is demonstrated on MNIST. :type learning_rate: float :param learning_rate: learning rate used (factor for the stochastic gradient :type L1_reg: float :param L1_reg: L1-norm's weight when added to the cost (see regularization) :type L2_reg: float :param L2_reg: L2-norm's weight when added to the cost (see regularization) :type n_epochs: int :param n_epochs: maximal number of epochs to run the optimizer :type dataset: string :param dataset: the path of the MNIST dataset file from http://www.iro.umontreal.ca/~lisa/deep/data/mnist/mnist.pkl.gz """ datasets = load_data(dataset) train_set_x, train_set_y = datasets[0] valid_set_x, valid_set_y = datasets[1] test_set_x, test_set_y = datasets[2] # compute number of minibatches for training, validation and testing n_train_batches = train_set_x.get_value(borrow=True).shape[0] / batch_size n_valid_batches = valid_set_x.get_value(borrow=True).shape[0] / batch_size n_test_batches = test_set_x.get_value(borrow=True).shape[0] / batch_size ###################### # BUILD ACTUAL MODEL # ###################### print '... building the model' # allocate symbolic variables for the data index = T.lscalar() # index to a [mini]batch x = T.matrix('x') # the data is presented as rasterized images y = T.ivector('y') # the labels are presented as 1D vector of # [int] labels rng = numpy.random.RandomState(1234) # construct the MLP class classifier = MLP(rng=rng, input=x, n_in=28 * 28, n_hidden=n_hidden, n_out=10) # the cost we minimize during training is the negative log likelihood of # the model plus the regularization terms (L1 and L2); cost is expressed # here symbolically cost = classifier.negative_log_likelihood(y) + L1_reg * classifier.L1 + L2_reg * classifier.L2_sqr # compiling a Theano function that computes the mistakes that are made # by the model on a minibatch test_model = theano.function(inputs=[index], outputs=classifier.errors(y), givens={ x: test_set_x[index * batch_size:(index + 1) * batch_size], y: test_set_y[index * batch_size:(index + 1) * batch_size]}) validate_model = theano.function(inputs=[index], outputs=classifier.errors(y), givens={ x: valid_set_x[index * batch_size:(index + 1) * batch_size], y: valid_set_y[index * batch_size:(index + 1) * batch_size]}) # compute the gradient of cost with respect to theta (sotred in params) # the resulting gradients will be stored in a list gparams gparams = [] for param in classifier.params: gparam = T.grad(cost, param) gparams.append(gparam) # specify how to update the parameters of the model as a list of # (variable, update expression) pairs updates = [] # given two list the zip A = [a1, a2, a3, a4] and B = [b1, b2, b3, b4] of # same length, zip generates a list C of same size, where each element # is a pair formed from the two lists : # C = [(a1, b1), (a2, b2), (a3, b3), (a4, b4)] for param, gparam in zip(classifier.params, gparams): updates.append((param, param - learning_rate * gparam)) # compiling a Theano function `train_model` that returns the cost, but # in the same time updates the parameter of the model based on the rules # defined in `updates` train_model = theano.function(inputs=[index], outputs=cost, updates=updates, givens={ x: train_set_x[index * batch_size:(index + 1) * batch_size], y: train_set_y[index * batch_size:(index + 1) * batch_size]}) ############### # TRAIN MODEL # ############### print '... training' # early-stopping parameters patience = 10000 # look as this many examples regardless patience_increase = 2 # wait this much longer when a new best is # found improvement_threshold = 0.995 # a relative improvement of this much is # considered significant validation_frequency = min(n_train_batches, patience / 2) # go through this many # minibatche before checking the network # on the validation set; in this case we # check every epoch best_params = None best_validation_loss = numpy.inf best_iter = 0 test_score = 0. start_time = time.clock() epoch = 0 done_looping = False while (epoch < n_epochs) and (not done_looping): epoch = epoch + 1 for minibatch_index in xrange(n_train_batches): minibatch_avg_cost = train_model(minibatch_index) # iteration number iter = (epoch - 1) * n_train_batches + minibatch_index if (iter + 1) % validation_frequency == 0: # compute zero-one loss on validation set validation_losses = [validate_model(i) for i in xrange(n_valid_batches)] this_validation_loss = numpy.mean(validation_losses) print('epoch %i, minibatch %i/%i, validation error %f %%' % (epoch, minibatch_index + 1, n_train_batches, this_validation_loss * 100.)) # if we got the best validation score until now if this_validation_loss < best_validation_loss: #improve patience if loss improvement is good enough if this_validation_loss < best_validation_loss * improvement_threshold: patience = max(patience, iter * patience_increase) best_validation_loss = this_validation_loss best_iter = iter # test it on the test set test_losses = [test_model(i) for i in xrange(n_test_batches)] test_score = numpy.mean(test_losses) print((' epoch %i, minibatch %i/%i, test error of ' 'best model %f %%') % (epoch, minibatch_index + 1, n_train_batches, test_score * 100.)) if patience <= iter: done_looping = True break end_time = time.clock() print(('Optimization complete. Best validation score of %f %% ' 'obtained at iteration %i, with test performance %f %%') % (best_validation_loss * 100., best_iter + 1, test_score * 100.)) print >> sys.stderr, ('The code for file ' + os.path.split(__file__)[1] + ' ran for %.2fm' % ((end_time - start_time) / 60.)) if __name__ == '__main__': test_mlp()